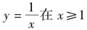-
1.1序
-
1.2前 言
-
1.3第1章 概论
-
1.3.1§1.1 关于数学文化
-
1.3.2§1.2 数学与数学教育
-
1.3.3§1.3 数学分支巡礼
-
1.3.4§1.4 数学建模与数学建模竞赛
-
1.4第2章 数论与数学文化
-
1.4.1§2.1 数论预备知识简介
-
1.4.2§2.2 数字美学欣赏
-
1.4.3§2.3 再叙数论——数学之皇后
-
1.5第3章 毕达哥拉斯与勾股定理
-
1.5.1§3.1 勾股定理
-
1.5.2§3.2 古希腊数学与人类文明
-
1.5.3§3.3 附录
-
1.6第4章 斐波纳契数列与黄金比
-
1.6.1§4.1 斐波纳契数列
-
1.6.2§4.2 黄金分割(黄金比,黄金数)
-
1.6.3§4.3 连分数及其应用
-
1.7第5章 幻方文化——数学文化的起源
-
1.7.1§5.1 幻方基本知识
-
1.7.2§5.2 妙趣横生的幻方
-
1.7.3§5.3 幻方的应用
-
1.7.4§5.4 附录
-
1.8第6章 数学问题、数学猜想与数学发展
-
1.8.1§6.1 关于数学猜想
-
1.8.2§6.2 哥德巴赫猜想
-
1.8.3§6.3 费尔马大定理(费尔马最后定理)
-
1.8.4§6.4 地图上的数学文化
-
1.8.5§6.5 世纪数学问题欣赏
-
1.8.6§6.6 附录
-
1.9第7章 数学悖论——从不和谐到和谐
-
1.9.1§7.1 数学的和谐
-
1.9.2§7.2 数学悖论
-
1.9.3§7.3 数学大厦基础上的裂缝——三次数学危机
-
1.9.4§7.4 数学哲学
-
1.9.5§7.5 附录
-
1.10第8章 变量数学的产生与发展
-
1.10.1§8.1 笛卡儿和费尔马的解析几何思想
-
1.10.2§8.2 微积分的创立与发展
-
1.10.3§8.3 再说牛顿
-
1.11第9章 中国古代数学文化
-
1.11.1§9.1 《九章算术》及其文化内涵
-
1.11.2§9.2 贾宪三角及其美学意义
-
1.11.3§9.3 《算经十书》之文化内涵
-
1.11.4§9.4 附录
-
1.12第10章 走出来的数学文化
-
1.12.1§10.1 七桥问题与拓扑学
-
1.12.2§10.2 欧拉回路与中国邮递员问题
-
1.12.3§10.3 读读欧拉
-
1.12.4§10.4 附录
-
1.13第11章 分形艺术欣赏
-
1.13.1§11.1 从数学怪物谈起
-
1.13.2§11.2 分形几何学
-
1.13.3§11.3 分形艺术欣赏
-
1.13.4§11.4 分形理论在经济研究中的应用及优势
-
1.14参考文献
1
数学文化欣赏