伽利略对自由落体的研究

在科学上没有平坦大道，物理学经历的是一条曲折艰难的道路，在创建物理学的过程中许多著名物理学家作出了丰功伟绩，他们中有一些往往被看成是圣人。年轻的朋友们也许不了解他们的奋斗经历，以为他们都是些天才，普通人望尘莫及。

读者们可能都很熟悉伽利略的生平和贡献，可能他正是大家崇拜的偶像。然而大家也许不知道，他经历的是一条非常曲折的道路。伽利略有许多发现、发明和创造。在这里，我们不说伽利略如何发明天文望远镜、如何制造第一支温度计、如何发现木星有卫星、太阳有黑子，也不说伽利略如何研究材料性质和浮力理论，单说伽利略是怎样发现落体运动定律的，他如何发扬古希腊学者阿基米德的风格，把实验研究与理论思辨结合起来，走出了一条科学发展的新路。

伽利略是意大利人，1564年出生在一个贵族家庭里，从小爱好文艺和科学。他所处的时代正值文艺复兴之后思想大解放的时期，意大利是文艺复兴的发源地，思想非常活跃。前面说过其杰出代表达·芬奇不仅是艺术家和工程师，还做过许多物理实验，主张在科学工作中多进行实验观察；波兰人哥白尼（1473—1543）主张日心说，公开向亚里士多德的信仰者挑战；英国人弗兰西斯·培根（1561—1626）大力宣传实验的重要性，极力反对经院哲学，为伽利略的工作鸣锣开道，可以说，他们是伽利略工作的前驱。

伽利略有两本名著，一本叫《关于托勒密和哥白尼两大世界体系的对话》（简称《两大世界体系》，1632年出版），另一本叫《关于力学和运动两门新科学的谈话》（简称《两门新科学》，1638年出版），在这两本书里伽利略有力地批判了亚里士多德的宇宙学说，为力学的发展奠定了思想基础。

伽利略研究落体理论对破除传统的亚里士多德的运动理论起过很关键的作用。据说，他曾登上比萨斜塔当众表演落体实验，他将大小相同的两个球，一轻一重，同时释放，结果两球同时落地。有人说，伽利略表演的那一天，比萨斜塔下热闹非凡，伽利略在其他教授和全体学生面前从比萨斜塔之顶反复地做了实验来证明这一点，通过这一实验把亚里士多德的运动理论批驳得体无完肤。事实是怎样的呢？落体实验对批驳亚里士多德的落体理论的确起过重要的作用，但最早的落体实验并不是伽利略做的，据史料记载，早在1586年就有人从高处做过落体实验，并对亚里士多德的教义提出质疑，那是荷兰人斯梯文。究竟伽利略有没有做过落体实验呢？经查考，在伽利略早年（1591）写的《论运动》（De－Motu）的小册子中确实提到过这类实验。直到伽利略去世二百年后，即1842年，才整理发表，不过他提到的实验不像人们所说的，是要彻底批驳亚里士多德的落体理论，而是为了弥补亚里士多德理论的缺陷。伽利略在这本小册子里用阿基米德的浮力定律来说明在媒质中落体的运动。伽利略当时显然仍然相信，同样大小的物体在空气中下落，较重的比较轻的快。

他写道：“如果从塔上落下两个同体积的球，其中之一比另一重一倍，我们会发现重的到达地面并不比轻的快一倍。其实，在运动开始时，轻物会走在重物的前面，在一段距离内要比重物快。”这就是伽利略自己记述的落体实验。

究竟伽利略是随便说说，还是真做了实验？从实验得到了什么结论？他在实验中是否真的看到了轻物先于重物下落？这个问题一直是个悬案。

1983年，有两个美国人做了两球同时下落的实验。他们用高速摄影机拍照，果然重现了伽利略观察到的现象，不过他们不是用机械释放两球，而是用两手分别握着两个球，并且必须手心向下，同时释放。他们根据实验判断，伽利略得到轻物走在重物前面的结论，是由于他握重球的手握得更紧，释放时略为缓慢所致。这件事说明了，伽利略确实是做过落体实验，不过他的实验不很成功，他的方法也欠高明，导致了错误的结论。同时也说明了，伽利略的思想不是从天上掉下来的，他经历了曲折的摸索过程。开始，他甚至还是亚里士多德的维护者。

然而，伽利略继续研究落体运动，逐步建立了科学的理论体系。他用速度和加速度的概念，分析了匀速运动和匀加速运动，对自由落体作了一些假设，并在假设的基础上进行了数学逻辑推理。他用几何学的方法由匀加速运动的速度公式υ＝at推出路程公式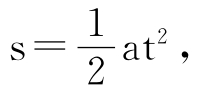再对路程s和时间t的关系进行实验检验。

伽利略高明的地方就在于他并不直接测量落体下落的距离和相应的时间，因为物体下落越来越快，下落时间很难测准，于是，他用了一块斜面，让小球沿斜面下滚，测小球滚下的时间和距离。这样由于斜面上物体所受作用力只是重力沿斜面的分力，就相当于冲淡了引力，速度和加速度都按比例减小，时间也就延缓了。难测量的量变成为容易测的量，测不准的量变成了能测准的量。

伽利略在他的著作《两门新科学》中对这个实验描述得十分具体，他写道：

“取长约12库比（1库比＝45．7厘米）、宽约半库比，厚约三指的木板，在边缘上刻一条一指多宽的槽，槽非常平直，经过打磨，在直槽上贴羊皮纸，尽可能使之平滑，然后让一个非常圆的、硬的光滑黄铜球沿槽滚下，我们将木板的一头抬高一二库比，使之略呈倾斜，再让铜球滚下，用下述方法记录球滚下所需时间。我们不止一次重复这一实验，使两次观测的时间相差不致超过脉搏的1／10。在完成这一步骤并确证其可靠性之后，就让铜球滚下全程的1／4，并测出下降时间，我们发现它刚好是滚下全程所需时间的一半。接着我们对其他距离进行实验，用滚下全程时间同滚下一半距离、2／3距离、3／4距离或任何部分距离所用时间进行比较。这样的实验重复了整整一百次，我们往往发现，经过的空间距离恒与所用时间的平方成正比例。这对于平面（也即铜球下滚的槽）的各种斜度都成立。我们也观测到，对于不同的斜度，下降的时间相互间的关系正如作者预计并证明过的比例一样。”

“为了测量时间，我们把一只盛水的大容器置于高处，在容器底部焊上一根口径很细的管子，用小杯子收集每次下降时由细管流出的水，不管是全程还是全程的一部分，都可以收集到。然后用极精密的天平称水的重量，这些水重之差和比值就给出时间之差和比值。精确度如此之高，以至于重复许多遍，结果都没有明显的差别。”

伽利略是怎样领悟到落体定律中的时间平方关系的呢？还要拉回到伽利略对亚里士多德运动理论的批判。

在《两门新科学》中，伽利略借他的化身萨尔维阿蒂的谈话，批驳物体下落速度与重量成正比的说法：

“萨：如果我们取两个自然速率不同的物体，把两者连在一起，快者将被慢者拖慢，慢者将被快者拖快。您同意我的看法吗？

辛：毫无疑问。您是对的。

萨：但是假如这是真的，并且假如大石头以8的速率运动，而小石头以4的速率运动，两石头在一起时，系统将以小于8的速率运动，但是两块石头拴在一起变得比原先速率为8的石头更大，所以更重的物体反而比更轻的物体运动慢，这个效果与您的设想相反。”

就这样，伽利略雄辩地揭露了速度与重量成正比的说法是荒谬的。

接着，伽利略又否定了亚里士多德把运动分成自然运动和强迫运动的分类方法，而是从运动的基本特征量：速度和加速度出发，把运动分成匀速运动和变速运动。他选择了最简单的变速运动来表示落体运动，这就是匀加速运动。

但是在定义匀加速运动时，他似乎走了一段弯路。起初，他也跟别人一样，假设下落过程中物体的速度与下落的距离成正比，他又是通过理想实验作出了正确的判断。他假设物体在落下第一段距离后已得到某二速度，于是在落下的距离加倍时，速度也应加倍。果真如此的话，则物体通过两段距离所用的时间将和通过第一段距离所用时间一样这显然是荒谬的。于是伽利略转而假设物体的速度与时间成正比，这样的假设是否正确，当然也要进行检验。

然而速度是难以直接测量的。于是伽利略借助于几何学的推导，得出s∞t²的关系，对于不同的时间比1：2：3：4……，物体下落的距离比为1：4：9：16……这些数字正是伽利略在那张实验记录上添加的第一列数字。从第一列数和第三列数的比例关系，伽利略证明沿斜面下降的物体在做匀加速运动。

伽利略发现落体运动定律有极其重要的意义。正如他在《两门新科学》中说的一句话：

“我们可以说，大门已经向新方法打开，这种将带来大量奇妙成果的新方法，在未来的年代里定会博得许多人的重视。”

伽利略真不愧为近代物理学的鼻祖。他的运动学研究不但建立了科学的落体定律，更为重要的是，他找到了一条物理学研究的必经之路。那就是把实验与数学推理结合在一起的物理学研究方法。

惯性定律是牛顿力学的重要基石之一，从亚里士多德的自然哲学转变到牛顿的经典力学，最深刻的变化就在于建立了惯性定律。亚里士多德认为一切物体的运动都是由于其他物体的作用；而牛顿则认为“每一个物体都会继续保持其静止或沿一直线做等速运动的状态，除非有力加于其上，迫使它改变这种状态。”这正是牛顿在《自然哲学的数学原理》一书中，作为第一条公理提出的基本力学原理。

牛顿在他的手稿《惯性定律片断》中写道：“所有那些古人知道第一定律，他们归之于原子在虚空中直线运动，因为没有阻力，运动极快而永恒。”这里所谓的古人，可以追溯到古希腊时代，当时德谟克利特（前460—前371）、伊壁鸠鲁（前342一前270）等著名学者都有这样的看法。例如，伊壁鸠鲁就说过：“当原子在虚空里被带向前进而没有东西与他们碰撞时，它们一定以相等的速度运动。”应该指出，不论是古希腊的哲学家还是后来他们的信徒，都无法证实这条原理，只能看成是猜测或推想的结果。

亚里士多德则断言，物体只有在一个推动者的直接接触下，才能保持运动，一旦推动者停止作用，或两者脱离接触，物体就会停止下来。这种说法似乎与经验没有矛盾，但是显然经不起推敲。例如，对于抛射体的运动，亚里士多德解释说，之所以抛射体在出手后还会继续运动，是由于手或机械在做抛物动作中同时也使靠近物体的空气运动，而空气再带动物体运动。但是，在亚里士多德的思辨中，不可避免地会出现漏洞。人们要问，空气对物体的运动也会有阻力作用，为什么有的时候推力大于阻力，有的时候阻力又会大于推力？尽管亚里士多德被奉为圣贤，他的学说在中世纪还是不断有人批驳，逐渐被新的见解所代替。

例如，6世纪希腊有一位学者叫菲洛彭诺斯对亚里士多德的运动学说就持批判态度。他认为抛体本身具有某种动力，只是靠这一动力，才推动物体继续前进，直到动力耗尽才趋于停止，这种看法后来发展为“冲力理论”。代表人物是英国牛津大学的威廉（1300—1350），他认为，运动并不需要外来推力，一旦运动起来就要永远运动下去。他写道：“运动并不能完全与永恒的物体区分开，因为当可以用较少的实体时，就无需用更多的实体……没有这一额外的东西，就可以对各种运动给予澄清。”例如，关于抛射体运动，他解释为：“当运动物体离开投掷者后，是物体靠自己运动，而不是被任何在它里面或与之有关的动力所推动，因为无法区分运动者和被推动者。”他举磁针吸铁为例，说明要使铁运动并不一定直接接触，并且还进一步设想，这种情况在真空中也能实现，可见亚里士多德认为真空不存在的说法是可疑的。

当然，威廉的说法并不等于惯性原理，但是却是走向惯性原理的重要步骤。因为，如果运动不需要原因，一旦发生就要永远持续，亚里士多德的推动说就要从根本上受到动摇。巴黎大学校长布里丹（1300～1358）也是批判亚里士多德运动学说的先行者。他反对空气是抛射体运动的推动者，亚里士多德对抛射体的解释是：在抛射体的后面形成了虚空区域，由于自然界惧怕虚空，于是就有空气立即填补了这一虚空区域，因而形成了推力。布里丹反问道：“空气又是受什么东西的推动呢？显然还有别的物体在起作用，这样一连串的推动根源何在呢？他举磨盘和陀螺为例，这些转动的物体在它们转动时无前后之分，一直保持着转动状态，并不需要外界的推动。两支标枪：一支两头尖，另一支一头尖一头钝，然而投掷时并不见得前者慢后者快。如果按照亚里士多德的解释，标枪之所以离手后继续飞行，是因为在其身后留出了虚空，空气填补虚空，对标枪造成推力，就应该对尖头和钝头有所区别。水手在船上，只感到迎面吹来的风，而不感到背后推动的风。按照亚里士多德的说法，水手会因空气填补虚空而在背面受到冲击。这些都说明：“空气持续推动抛射体”的说法不符合事实。于是布里丹提出“冲力理论”，他认为：“推动者在推动一物体运动时，便对它施加某种冲力或某种动力。”正是由于冲力或动力的作用，物体才得以继续运动。

布里丹的学生根据布里丹的思想发展了冲力理论，他们用冲力来说明落体的加速运动，认为速度越大，冲力也越大。一个有名的例子是这样的，假如把地球钻通，让一个重物落入洞里，直趋地心，显然当落体的重心到达地心时，该物体会越过地心，继续向前运动，因为冲力并未耗尽。而当冲力耗尽后，物体将回落。于是它围绕地心振荡，直到冲力不再存在，才重又静止下来。这样一个理想实验虽然难以验证，但是他们的解释还是能够自圆其说的。

冲力理论当然是不正确的。然而却比亚里士多德的运动理论前进了一大步。要知道，不论是伽利略，还是牛顿，都在自己的著作中留下了冲力理论的烙印。他们经过深入的思考，才逐步形成惯性的概念。

伽利略在自己的著作中多次提出类似于惯性原理的说法，例如在《关于托勒密和哥白尼两大世界体系的对话》（1632年）中，他写道：

“只要斜面延伸下去，球将无限地继续运动，而且在不断加速，因为运动着的重物的本性就是这样。”

再请读他的作品中的另一段对话：

“萨：……如果没有引起球体减速的原因……你认为球体会继续运动到多远呢？

辛：只要平面不上升也不下降，平面多长，球体就运动多远。

萨：如果这样一个平面是无限的，那么，在这个平面上的运动同样是无限的了，也就是说，永恒的了。……”

在另一本著作《两门新科学》（1638年）中，伽利略再次表述了惯性定律，他用小球的运动来说明他的见解。假设沿斜面AB落下的物体，以B点得到的速度沿另一斜面BC向上运动，则物体不受BC倾斜的影响仍将达到和A点同样的高度，只是达到最高点需要的时间不同而已。

但是，伽利略又同时认为，等速圆周运动也是惯性运动，并进而论证行星正是由于按圆周轨道做等速运动才能永恒地运转，而他的直线运动实际上只限于沿着水平面的运动，所以并没有正确地表达惯性定律。

1644年，笛卡儿（1596—1650）在《哲学原理》一书中弥补了伽利略的不足。他明确地指出，除非物体受到外因的作用，物体将永远保持其静止或运动状态，并且还特地声明，惯性运动的物体永远不会使自己趋向曲线运动，而只保持在直线上运动，他表述成两条定律：

（一）每一单独的物质微粒将继续保持同一状态，直到与其他微粒相碰被迫改变这一状态为止；

（二）所有的运动，其本身都是沿直线的。

有意思的是，笛卡儿的思想却是建立在一种信念之上的。他解释道：“这个规则……来自上帝是不朽的，他以最简单的方式保持自然中的运动。”

笛卡儿1629年在给友人麦森的信中就曾断言：“我假设，运动一旦加于物体，就会永远保持下去，除非受到某种外来手段的破坏。换言之，某一物体在真空中开始运动，将永远运动并保持同一速度。”

笛卡儿比其他人高明的地方就是认识到惯性定律是解决力学问题的关键所在，是他最早把惯性定律作为原理加以确立，并视之为整个自然观的基础，这对后来牛顿的综合工作有深远影响。

然而，笛卡儿只停留在概念的提出，并没有成功地解决力学体系问题。牛顿对惯性定律的认识却也经过了一番曲折，直到1687年撰写《自然哲学的数学原理》之际，才摆脱旧观念的束缚，把惯性定律作为第一原理正式提了出来。