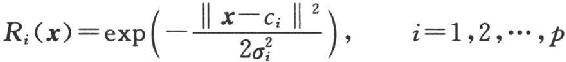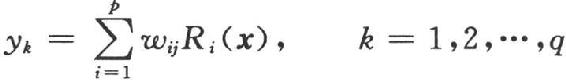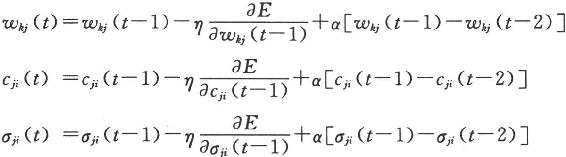模式识别与智能计算的MATLAB实现
-
1.1插页
-
1.2前言
-
1.3第1章 绪论
-
1.3.11.1 模式识别的基本概念
-
1.3.1.11.1.1 模式与模式识别的概念
-
1.3.1.21.1.2 模式的特征
-
1.3.1.31.1.3 模式识别系统
-
1.3.21.2 模式识别的主要方法
-
1.3.31.3 模式识别的主要研究内容
-
1.3.41.4 模式识别在科学研究中的应用
-
1.3.4.11.4.1 化合物的构效分析
-
1.3.4.21.4.2 谱图解析
-
1.3.4.31.4.3 材料研究
-
1.3.4.41.4.4 催化剂研究
-
1.3.4.51.4.5 机械故障诊断与监测
-
1.3.4.61.4.6 化学物质源产地判断
-
1.3.4.71.4.7 疾病的诊断与预测
-
1.3.4.81.4.8 矿藏勘探
-
1.3.4.91.4.9 考古及食品工业中的应用
-
1.4第2章 统计模式识别技术
-
1.4.12.1 基于概率统计的贝叶斯分类方法
-
1.4.1.12.1.1 最小错误率贝叶斯分类
-
1.4.1.22.1.2 最小风险率贝叶斯分类
-
1.4.22.2 线性分类器
-
1.4.2.12.2.1 线性判别函数
-
1.4.2.22.2.2 Fisher线性判别函数
-
1.4.2.32.2.3 感知器算法
-
1.4.32.3 非线性分类器
-
1.4.3.12.3.1 分段线性判别函数
-
1.4.3.22.3.2 近邻法
-
1.4.3.32.3.3 势函数法
-
1.4.3.42.3.4 SIMCA方法
-
1.4.42.4 聚类分析
-
1.4.4.12.4.1 模式相似度
-
1.4.4.22.4.2 聚类准则
-
1.4.4.32.4.3 层次聚类法
-
1.4.4.42.4.4 动态聚类法
-
1.4.4.52.4.5 决策树分类器
-
1.4.52.5 统计模式识别在科学研究中的应用
-
1.5第3章 人工神经网络及模式识别
-
1.5.13.1 人工神经网络的基本概念
-
1.5.1.13.1.1 人工神经元
-
1.5.1.23.1.2 传递函数
-
1.5.1.33.1.3 人工神经网络分类和特点
-
1.5.23.2 BP人工神经网络
-
1.5.2.13.2.1 BP人工神经网络学习算法
-
1.5.2.23.2.2 BP人工神经网络MATLAB实现
-
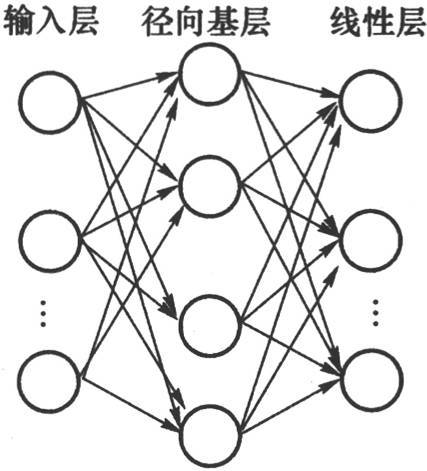
1.5.33.3 径向基函数神经网络RBF
-
1.5.3.13.3.1 RBF的结构与学习算法
-
1.5.3.23.3.2 RBF的MATLAB实现
-
1.5.43.4 自组织竞争人工神经网络
-
1.5.4.13.4.1 自组织竞争人工神经网络的基本概念
-
1.5.4.23.4.2 自组织竞争神经网络的学习算法
-
1.5.4.33.4.3 自组织竞争网络的MATLAB实现
-
1.5.53.5 对向传播神经网络CPN
-
1.5.5.13.5.1 CPN的基本概念
-
1.5.5.23.5.2 CPN网络的学习算法
-
1.5.63.6 反馈型神经网络Hopfield
-
1.5.6.13.6.1 Hopfield网络的基本概念
-
1.5.6.23.6.2 Hopfield网络的学习算法
-
1.5.6.33.6.3 Hopfield网络的MATLAB实现
-
1.5.73.7 人工神经网络技术在科学研究中的应用
-
1.6第4章 模糊系统理论及模式识别
-
1.6.14.1 模糊系统理论基础
-
1.6.1.14.1.1 模糊集合
-
1.6.1.24.1.2 模糊关系
-
1.6.1.34.1.3 模糊变换与模糊综合评判
-
1.6.1.44.1.4 If…then规则
-
1.6.1.54.1.5 模糊推理
-
1.6.24.2 模糊模式识别的基本方法
-
1.6.2.14.2.1 最大隶属度原则
-
1.6.2.24.2.2 择近原则
-
1.6.2.34.2.3 模糊聚类分析
-
1.6.34.3 模糊神经网络
-
1.6.3.14.3.1 模糊神经网络
-
1.6.3.24.3.2 模糊BP神经网络
-
1.6.44.4 模糊逻辑系统及其在科学研究中的应用
-
1.7第5章 核函数方法及应用
-
1.7.15.1 核函数方法
-
1.7.25.2 基于核的主成分分析方法
-
1.7.2.15.2.1 主成分分析
-
1.7.2.25.2.2 基于核的主成分分析
-
1.7.35.3 基于核的Fisher判别方法
-
1.7.3.15.3.1 Fisher判别方法
-
1.7.3.25.3.2 基于核的Fisher判别方法分析
-
1.7.45.4 基于核的投影寻踪方法
-
1.7.4.15.4.1 投影寻踪分析
-
1.7.4.25.4.2 基于核的投影寻踪分析
-
1.7.55.5 核函数方法在科学研究中的应用
-
1.8第6章 支持向量机及其模式识别
-
1.8.16.1 统计学习理论基本内容
-
1.8.26.2 支持向量机
-
1.8.2.16.2.1 最优分类面
-
1.8.2.26.2.2 支持向量机模型
-
1.8.36.3 支持向量机在模式识别中的应用
-
1.9第7章 可拓学及其模式识别
-
1.9.17.1 可拓学概论
-
1.9.1.17.1.1 可拓工程基本思想
-
1.9.1.27.1.2 可拓工程使用的基本工具
-
1.9.27.2 可拓集合
-
1.9.2.17.2.1 可拓集合含义
-
1.9.2.27.2.2 物元可拓集合
-
1.9.37.3 可拓聚类预测的物元模型
-
1.9.47.4 可拓学在科学研究中的应用
-
1.10第8章 粗糙集理论及其模式识别
-
1.10.18.1 粗糙集理论基础
-
1.10.1.18.1.1 分类规则的形成
-
1.10.1.28.1.2 知识的约简
-
1.10.28.2 粗糙神经网络
-
1.10.38.3 系统评估粗糙集方法
-
1.10.3.18.3.1 模型结构
-
1.10.3.28.3.2 综合评估方法
-
1.10.48.4 粗糙集聚类方法
-
1.10.58.5 粗糙集理论在科学研究中的应用
-
1.11第9章 遗传算法及模式识别
-
1.11.19.1 遗传算法的基本原理
-
1.11.29.2 遗传算法分析
-
1.11.2.19.2.1 染色体的编码
-
1.11.2.29.2.2 适应度函数
-
1.11.2.39.2.3 遗传算子
-
1.11.39.3 控制参数的选择
-
1.11.49.4 模拟退火算法
-
1.11.4.19.4.1 模拟退火的基本概念
-
1.11.4.29.4.2 模拟退火算法的基本过程
-
1.11.4.39.4.3 模拟退火算法中的控制参数
-
1.11.59.5 基于遗传算法的模式识别在科学研究中的应用
-
1.11.5.19.5.1 遗传算法的MATLAB实现
-
1.11.5.29.5.2 遗传算法在科学研究中的应用实例
-
1.12第10章 蚁群算法及其模式识别
-
1.12.110.1 蚁群算法原理
-
1.12.1.110.1.1 基本概念
-
1.12.1.210.1.2 蚁群算法的基本模型
-
1.12.1.310.1.3 蚁群算法的特点
-
1.12.210.2 蚁群算法的改进
-
1.12.2.110.2.1 自适应蚁群算法
-
1.12.2.210.2.2 遗传算法与蚁群算法的融合
-
1.12.2.310.2.3 蚁群神经网络
-
1.12.310.3 聚类问题的蚁群算法
-
1.12.3.110.3.1 聚类数目已知的聚类问题的蚁群算法
-
1.12.3.210.3.2 聚类数目未知的聚类问题的蚁群算法
-
1.12.410.4 蚁群算法在科学研究中的应用
-
1.13第11章 粒子群算法及其模式识别
-
1.13.111.1 粒子群算法的基本原理
-
1.13.211.2 全局模式与局部模式
-
1.13.311.3 粒子群算法的特点
-
1.13.411.4 基于粒子群算法的聚类分析
-
1.13.4.111.4.1 算法描述
-
1.13.4.211.4.2 实现步骤
-
1.13.511.5 粒子群算法在科学研究中的应用
-
1.14第12章 可视化模式识别技术
-
1.14.112.1 高维数据的图形表示方法
-
1.14.1.112.1.1 轮廓图
-
1.14.1.212.1.2 雷达图
-
1.14.1.312.1.3 树形图
-
1.14.1.412.1.4 三角多项式图
-
1.14.1.512.1.5 散点图
-
1.14.1.612.1.6 星座图
-
1.14.1.712.1.7 脸谱图
-
1.14.212.2 图形特征参数计算
-
1.14.312.3 显示方法
-
1.14.3.112.3.1 线性映射
-
1.14.3.212.3.2 非线性映射
-
1.15第13章 灰色系统方法及应用
-
1.15.113.1 灰色系统的基本概念
-
1.15.1.113.1.1 灰数
-
1.15.1.213.1.2 灰数白化与灰度
-
1.15.213.2 灰色序列生成算子
-
1.15.2.113.2.1 均值生成算子
-
1.15.2.213.2.2 累加生成算子
-
1.15.2.313.2.3 累减生成算子
-
1.15.313.3 灰色分析
-
1.15.3.113.3.1 灰色关联度分析
-
1.15.3.213.3.2 无量纲化的关键算子
-
1.15.3.313.3.3 关联分析的主要步骤
-
1.15.3.413.3.4 其他几种灰色关联度
-
1.15.413.4 灰色聚类
-
1.15.513.5 灰色系统建模
-
1.15.5.113.5.1 GM(1,1)模型
-
1.15.5.213.5.2 GM(1,1)模型检验
-
1.15.5.313.5.3 残差GM(1,1)模型
-
1.15.5.413.5.4 GM(1,N)模型
-
1.15.613.6 灰色灾变预测
-
1.15.713.7 灰色系统的应用
-
1.16第14章 模式识别的特征及确定
-
1.16.114.1 基本概念
-
1.16.1.114.1.1 特征的特点
-
1.16.1.214.1.2 特征的类别
-
1.16.1.314.1.3 特征的形成
-
1.16.1.414.1.4 特征选择与提取
-
1.16.214.2 样本特征的初步分析
-
1.16.314.3 特征筛选处理
-
1.16.414.4 特征提取
-
1.16.4.114.4.1 特征提取的依据
-
1.16.4.214.4.2 特征提取的方法
-
1.16.514.5 基于K-L变换的特征提取
-
1.16.5.114.5.1 离散K-L变换
-
1.16.5.214.5.2 离散K-L变换的特征提取
-
1.16.5.314.5.3 吸收类均值向量信息的特征提取
-
1.16.5.414.5.4 利用总体熵吸收方差信息的特征提取
-
1.16.614.6 因子分析
-
1.16.6.114.6.1 因子分析的一般数学模型
-
1.16.6.214.6.2 Q型和R型因子分析
-
1.17参考文献