图1

我们一起开始今天的学习吧！

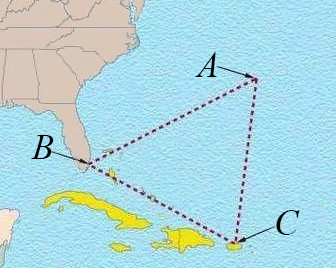
图2

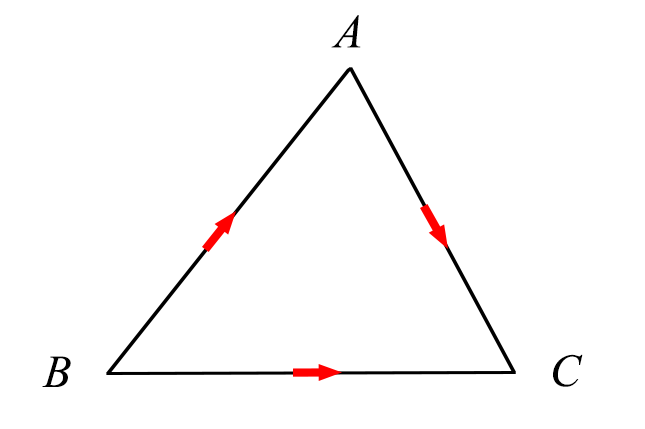
一条线路是由点B到点C；另一条路线是由点B到点A，再由点A到点C.         两条路线的长怎样表示呢？两条路线的长分别是BC，AB＋AC，两条路线的长有什么关系？为什么？

由“两点之间，线路最短”可以得到： AB＋AC＞BC ,         ① 同理有：            AC＋BC＞AB ,         ② AB＋BC＞AC ,         ③ 一般地，我们有： 三角形两边的和大于第三边. 由不等式②③移项可得：  BC＞AB-AC，BC＞AC-AB. 这就是说，三角形两边的差小于第三边.

（1）3 ,  6 ,  10；    （2）3 ,  5 ,  8；    （3）2.5 ,  3 ,  5 ； （4）a²＋3， a²＋4， a²＋7（a≠0）;  （5）3a，5a，8a（a＞0）.

根据三角形的三边关系可知：

（1）∵ 3＋6＜10，

      ∴三条线段不能组成三角形； 

（2）∵ 3＋5=8，

      ∴三条线段不能组成三角形；

（3）∵2.5＋3＞5，

      ∴三条线段能组成三角形；

（4）∵a≠0，

      ∴a²＞0.

      ∵（a²＋3）＋（a²＋4）＝2a²＋7

      ＝（a²＋7）＋a² ,

      ∴（a²＋3）＋（a²＋4）＞a²＋7.

      ∴三条线段能组成三角形；

（5）∵3a+5a=8a ,

      ∴三条线段不能组成三角形 .

判断三条线段能否组成三角形，首先找出最大边，然后用较小两边之和与最大边比较，若较小两边之和大于最大边，则能组成三角形，否则不能组成三角形.

当无法判断三角形三边之间大小关系时，要考虑所有可能的情况，并逐个验证.

若设第三边的长为x，根据三角形的三边关系可知，            8-3＜x＜8＋3            即5＜x＜11           ∵x为奇数           ∴x＝7或9，故选D.

当已知三角形两边长时，可求出第三边长的取值范围，

如：已知三角形两边为a，b（a＞b），第三边为x，则a-b＜x＜a+b.

现在我们就能帮李师傅解决刚开始提出的问题了，第三根木条的长只要大于5cm且小于13cm就可以围成一个三角形.