图1

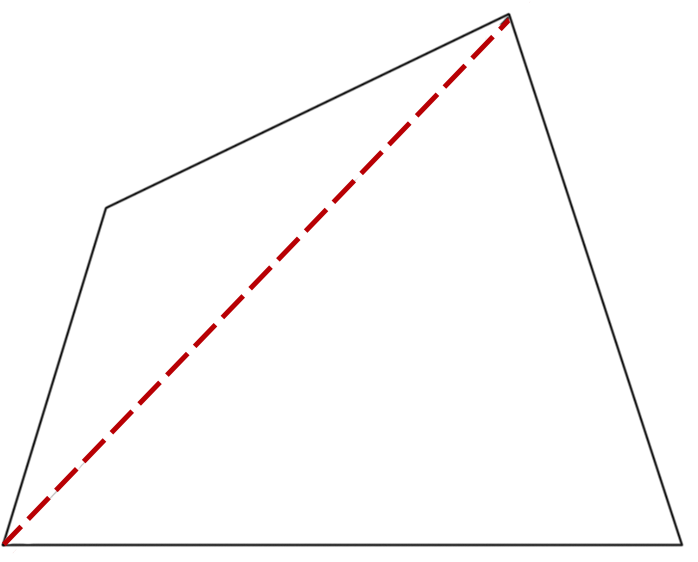
1.我们知道,三角形的内角和等于180°,正方形、长方形的内角和都等于360°,那么,任意一个四边形的内角和是否也等于360°呢? 如图2,从四边形的一个顶点出发,可以作1条对角线,它们将四边形分成2个三角形,四边形的内角和等于180°×2.
图2 |
归纳:四边形的内角和等于360°.

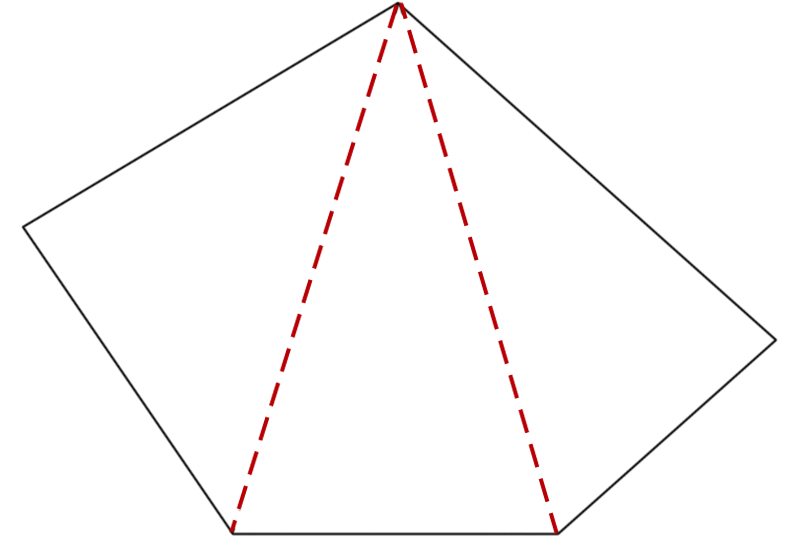
类比上面的过程,你能推导出五边形和六边形的内角和各是多少吗? 如图3,从五边形的一个顶点出发,可以作2条对角线,它们将五边形分为3个三角 形,五边形的内角和等于180°×3.
图3 |

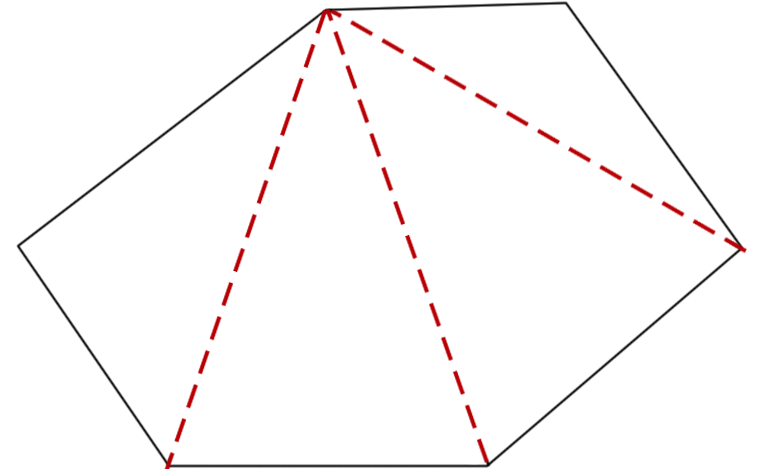
如图4,从六边形的一个顶点出发,可以作3条对角线,它们将六边形分为4个三角形,六边形的内角和等于180°×4.
图4 |

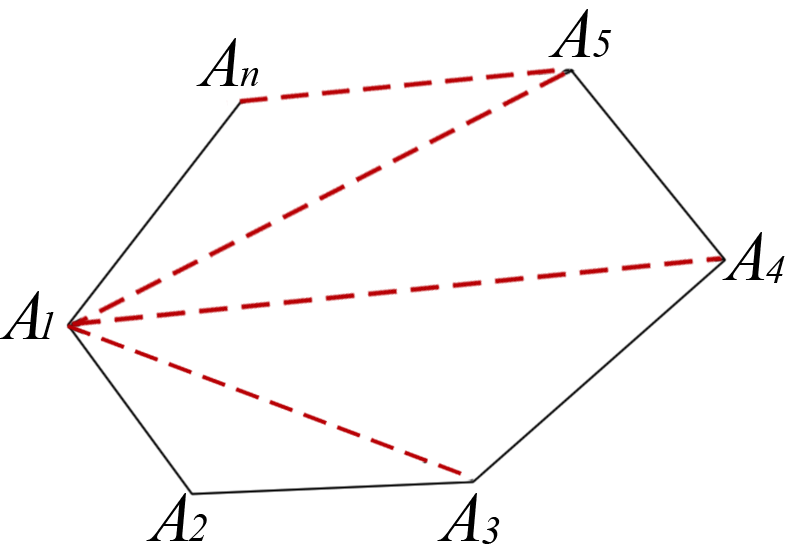
如图5,从n边形的一个顶点出发可以作(n-3)条对角线,它们将n边形分成(n-2)个三角形,n边形的内角和等于180°×(n-2).
图5 |
![]()
多边形内角和公式:n边形的内角和等于(n-2)×180°.
![]()
把一个多边形分成几个三角形,还有其他分法吗?由新的方法,能得出多边形内角和公式吗? |

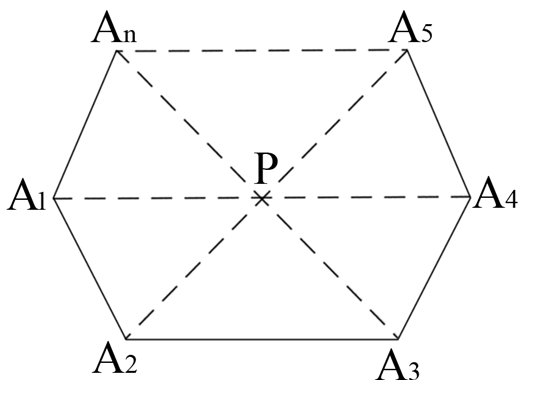
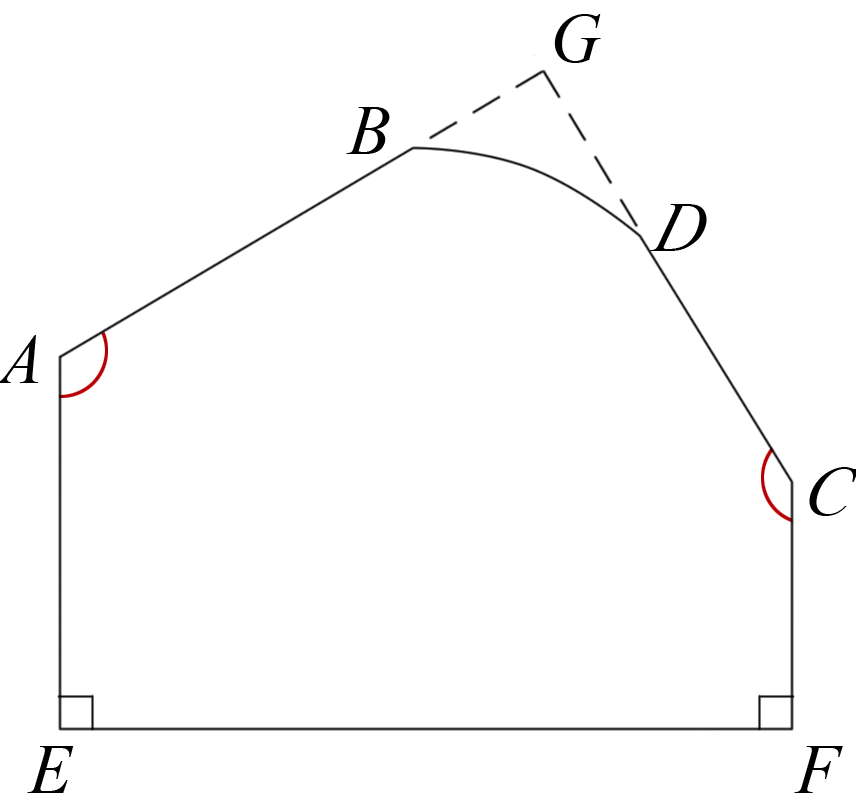
图6

图7
现在,我们就能解决课前提出的问题了. ∠AGC=(5-2)×180°-90°-90°-122°-155° = 540°-90°-90°-122°-155° = 83° ∴模板不合格. |

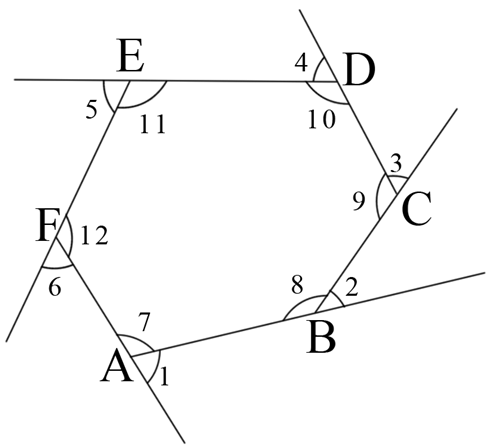
图8
∵ ∠1+∠7=180°, ∠2+∠8=180°, ∠3+∠9=180°, ∠4+∠10=180°, ∠5+∠11=180°, ∠6+∠12=180°, (六边形的任何一个外角加上与它相邻的内角都等于180°) ∴(∠1+∠2+∠3+∠4+∠5+∠6)+(∠7+∠8+∠9+∠10+∠11+∠12)=6×180°. (六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°) (这个总和就是六边形的外角和加上内角和) ∵∠7+∠8+∠9+∠10+∠11+∠12=(6-2)×180°, ∴∠1+∠2+∠3+∠4+∠5+∠6 = 6×180°-(6-2)×180° = 360°. (外角和等于总和减去内角和) |
把上述问题中的六边形换为n边形(n是不小于3的任意整数),有n×180°-(n-2)×180°= 360°.
![]()
| 多边形的外角和等于360°. |


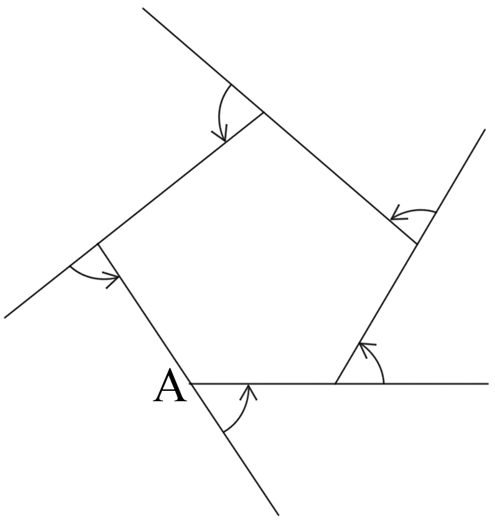
图9
在行程过程中所转的各个角的和,就是多边形的外交和,因此这一过程中转了360°.