前面我们学过直角三角形,今天根据三角形内角和定理对直角三角形作进一步的研究。
![]()

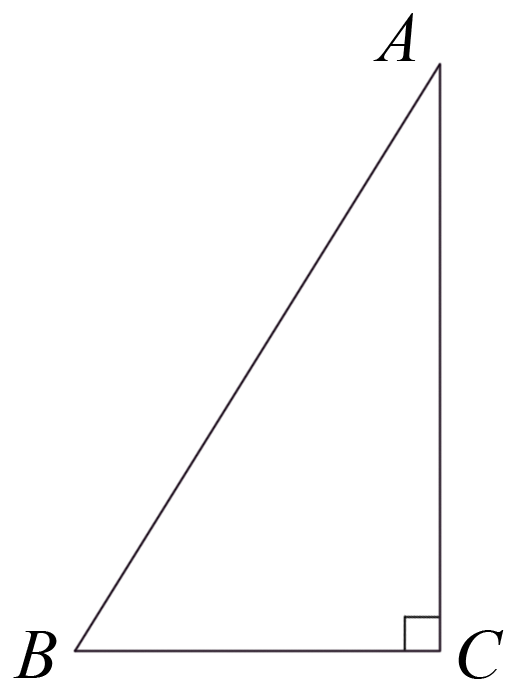
由三角形内角和定理, 得∠A+∠B+∠C =180°, ∴∠A+∠B+90°=180°, ∴∠A+∠B=90°. 图1 |
![]()
直角三角形的性质:直角三角形的两个锐角互余. |
2. 直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt△ABC.
![]()

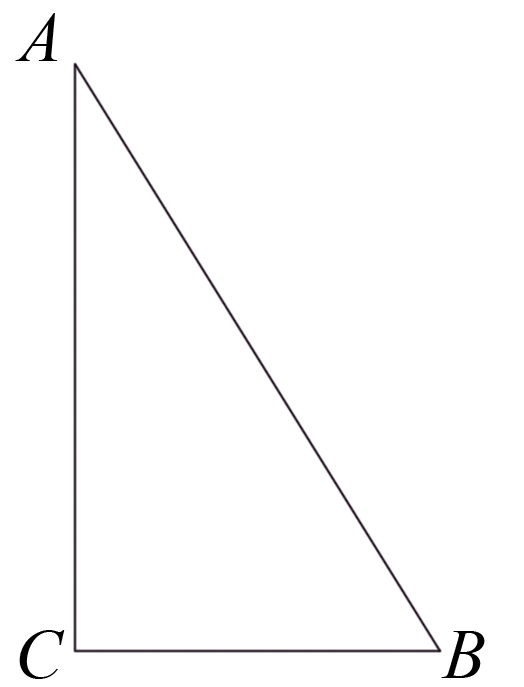
由三角形内角和定理, 得∠A+∠B+∠C =180°, ∵∠A+∠B=90°, ∴90°+∠C=180°, ∴∠C=90°.
图2 |
![]()
直角三角形的判定:有两个角互余的三角形是直角三角形. |

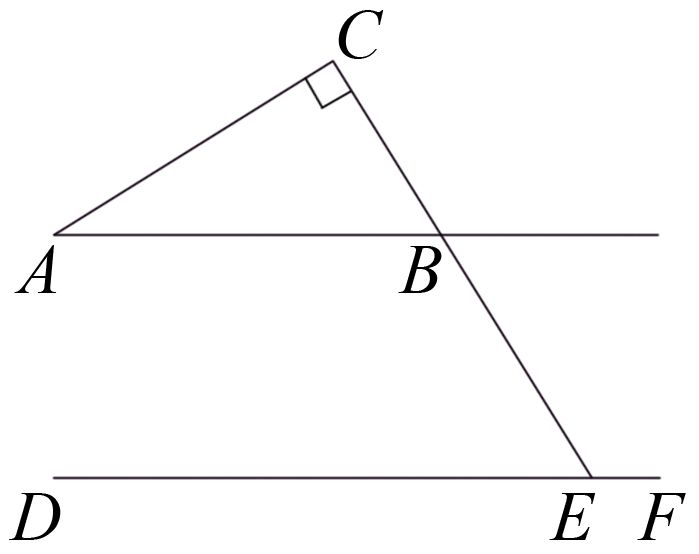
图3

∵AC⊥BC, ∴∠C=90°. ∴△ABC是直角三角形. ∵∠A=20°, ∴∠ABC=90°-∠A =90°-20°= 70°. ∵∠ABC+∠ABE=180°, ∴∠ABE=180°-∠ABC =180°-70°=110°. ∵AB∥DF, ∴∠CEF=∠ABE=110°. 这道题还能用其他方法解决,同学们可以尝试去完成. |