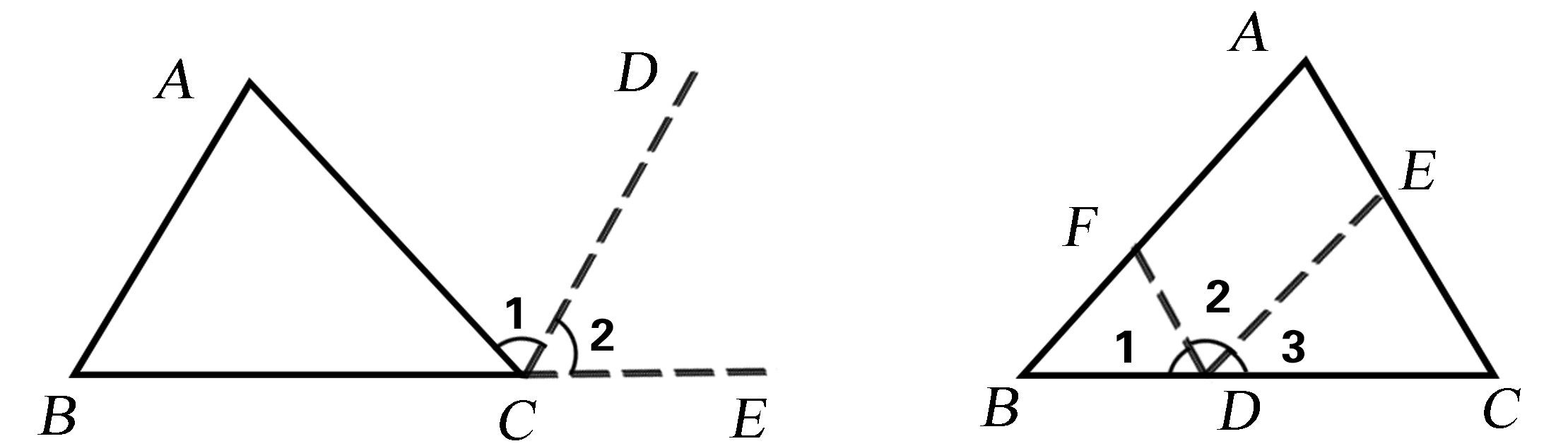我们知道,任意一个三角形的内角和等于180°,怎样证明这个结论的正确性呢?小学我们通过度量或剪拼的方法进行过验证,但我们不可能对所有的三角形进行验证,有没有一种能证明任意三角形的内角和等于180°的方法呢?

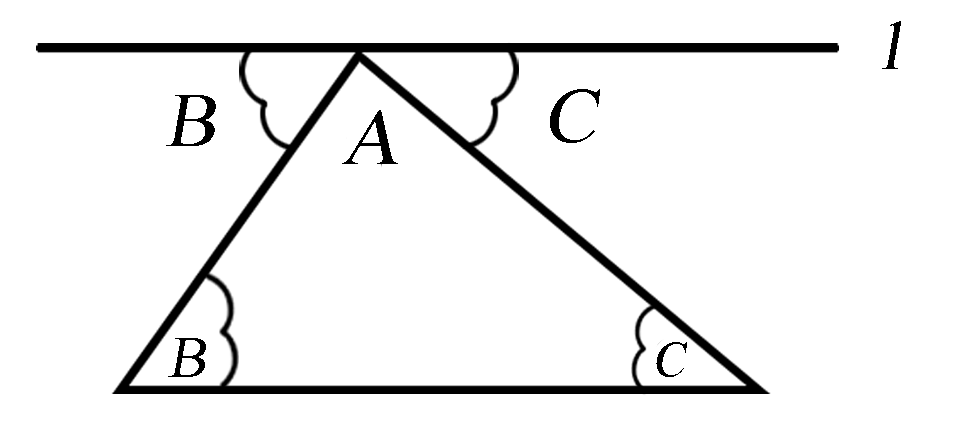
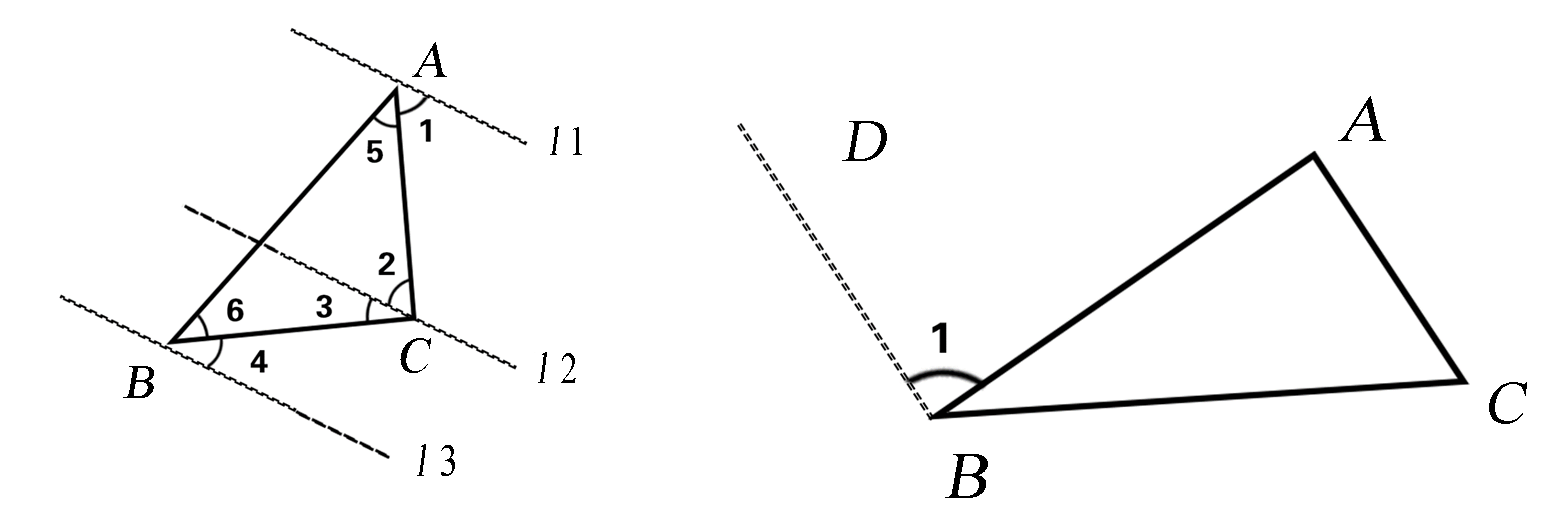
如图1,由内错角相等可得,移动后的∠B的一条边平行于边BC,同理,移动后的∠C的一条边平行于边BC.由“经过直线外一点,有且只有一条直线与这条直线平行”,可得移动后的∠B的一条边与移动后∠C的一条边在同一条直线上,并且这条直线平行于边BC.
图1 |
下面我们完成证明过程.
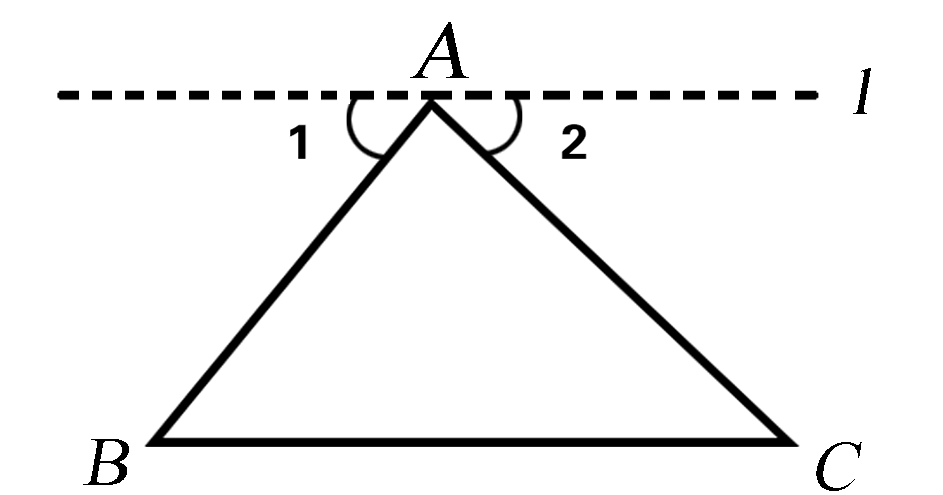
求证:∠A+∠B+∠C=180°. 证明:如图2,过点A作l∥BC. ∵l∥BC, ∴∠1=∠B, ∠2=∠C. (两直线平行,内错角相等) ∵∠BAC+∠1+∠2=180°(平角定义), 图2 ∴∠BAC+∠B+∠C=180°(等量代换). |
以上我们就证明了任意一个三角形的内角和都等于180°,得到如下定理:
三角形内角和定理:三角形三个内角的和等于180°.
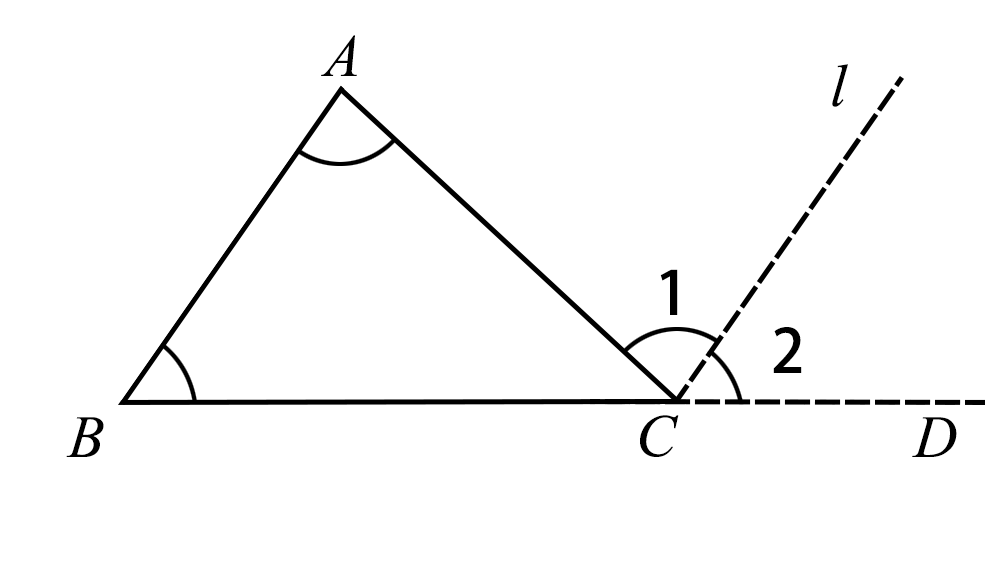
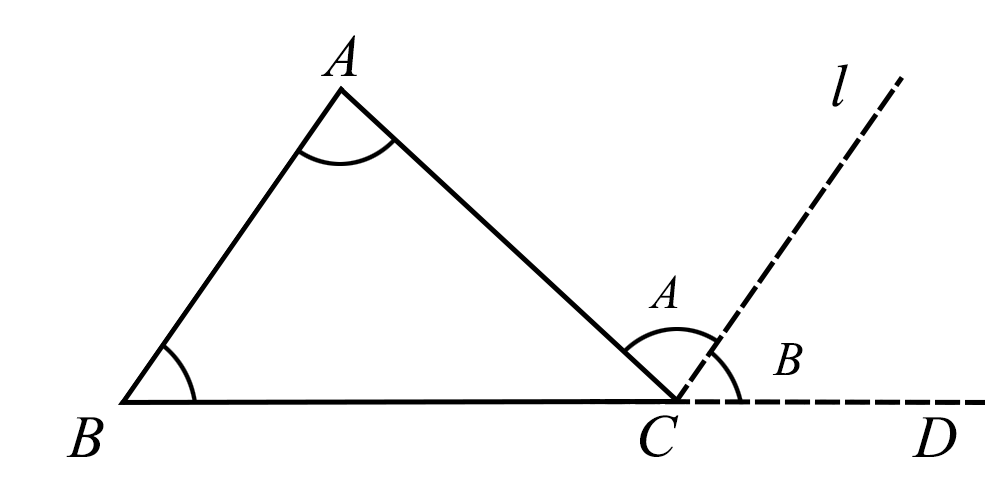 不难看出,移动后的∠B的一条边是BC的延长线,移动后的∠A和∠B各有一条边在l上,并且l平行于AB,于是得到证明三角形内角和等于180°的另一个方法. 图3 |
已知:△ABC(如图4). 求证:∠A+∠B+∠C=180°. 证明:如图4,延长BC,过点C作l∥AB. ∵l∥AB, ∴∠1=∠A. (两直线平行,内错角相等) ∠2=∠B. (两直线平行,内错角相等) ∵∠1+∠2+∠ACB=180°, (平角定义) 图4 ∴∠A+∠B+∠ACB=180°(等量代换).
|
(1) 利用两直线平行,内错角相等,将△ABC的三个内角转化为一个平角.(图5)
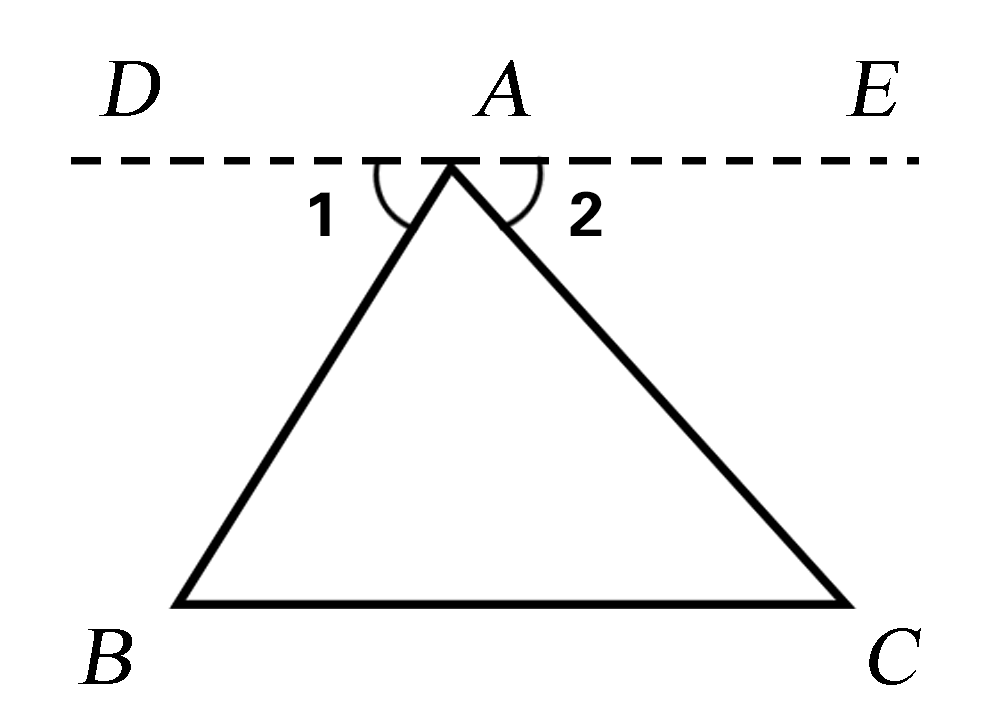
图5
(2) 利用两直线平行,内错角及同位角相等,将△ABC的三个内角转化为一个平角. (图6,图7)
图6 图7
(3)利用两直线平行,内错角相等,将△ABC的三个内角转化为一组同旁内角. (图8,图9)
图8 图9
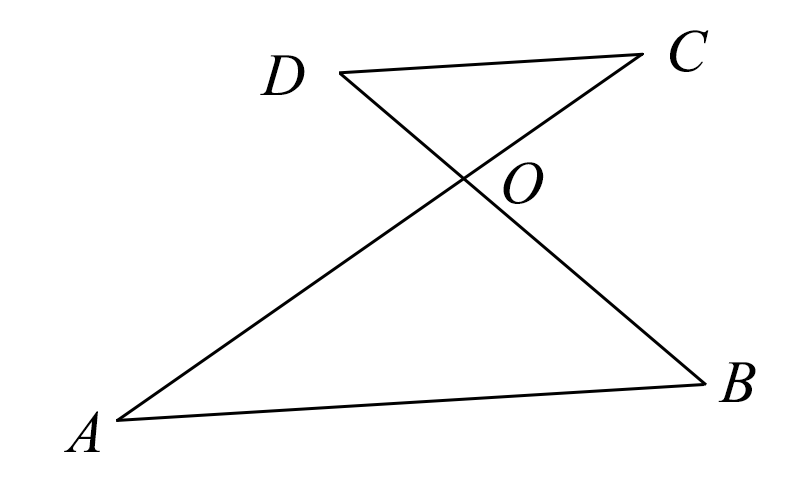
![]()
∵ AB∥CD, ∴∠C =∠A . ∵∠A =30°, ∴∠C =30°. ∵∠COD=105°, ∴∠D =180°-∠C-∠COD =180°-30°-105° 图10 =45°. |