课前预习微视频:三角形的中线
上一节
下一节



图1
今天我们学到的内容就会帮助大家解决这个问题.

图2



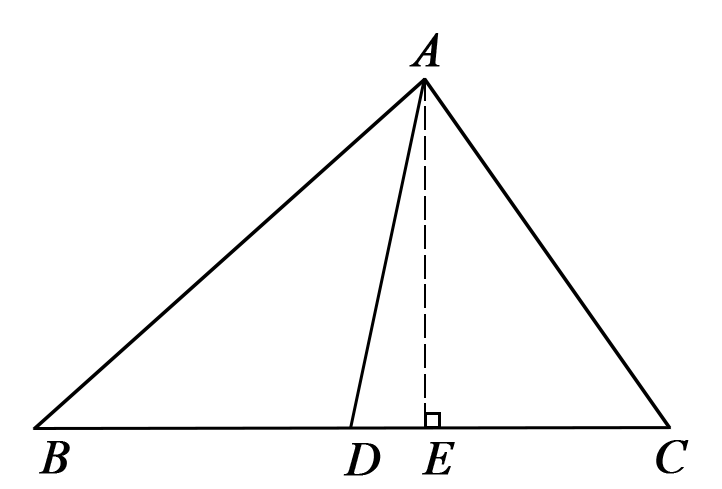
图3
如图3所示,AD是△ABC的中线,AE是△ABC的高,则S△ABD=1/2 BD·AE,S△ACD=1/2 CD·AE. ∵AD是△ABC的中线, ∴BD=CD. ∴S△ABD=S△ACD. ∵△ABD的周长为AB+BD+AD, △ACD的周长为AC+CD+AD, ∴△ABD的周长-△ACD的周长 =(AB+BD+AD)-(AC+CD+AD) =AB-AC. |
![]()
三角形每一条边上的中线将三角形分成面积相等的两个三角形,这两个三角形周长的差等于另两边长的差.
现在我们对课前提出的问题就有解决的办法了.

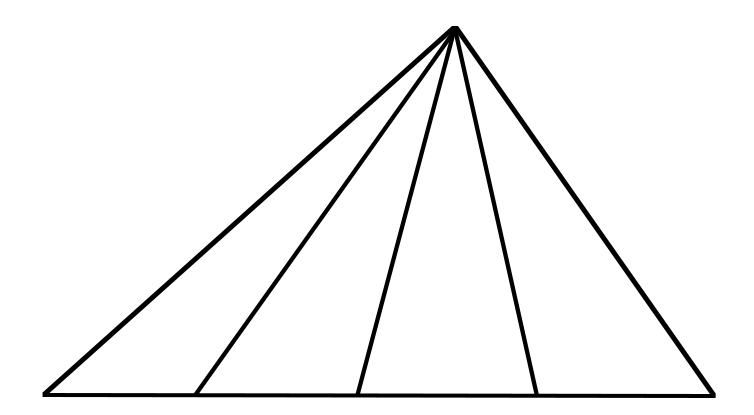
图4

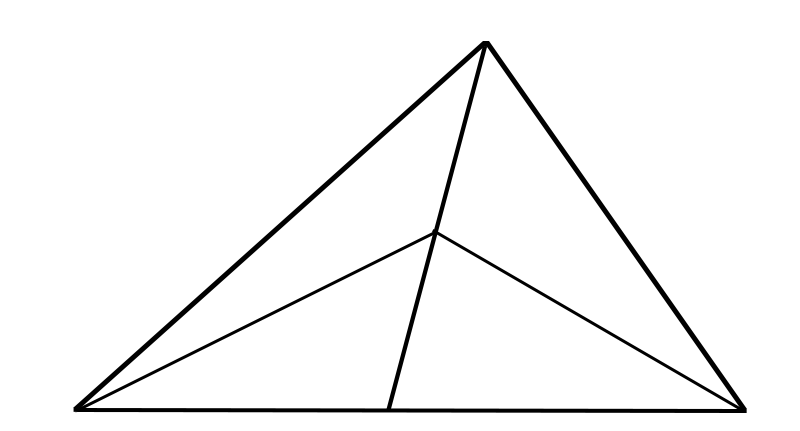
图5
方法

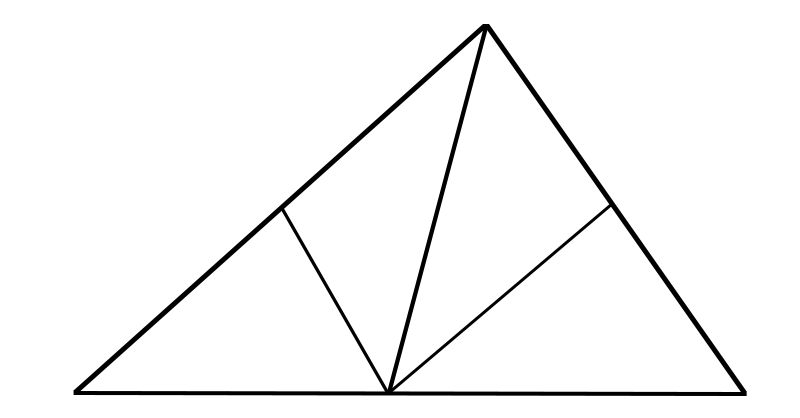
图6

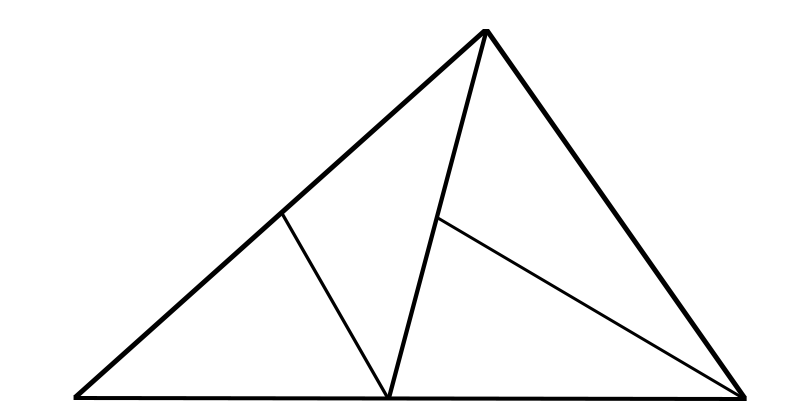
图7


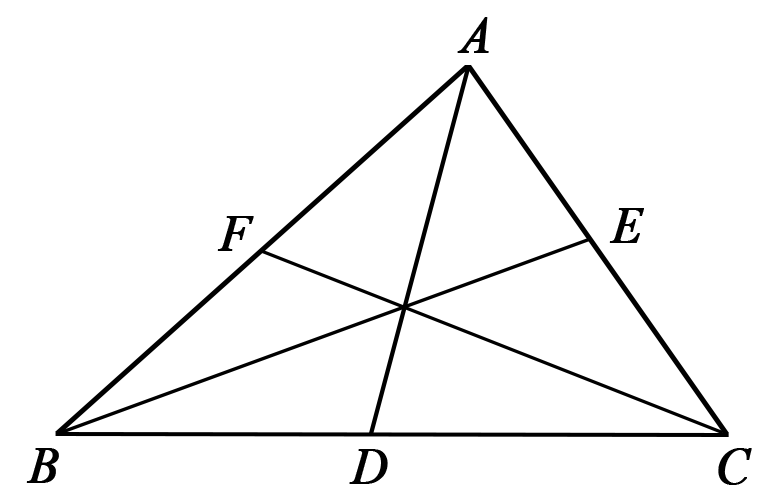
图8
三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.
![]()
任何三角形都有三条中线,三条中线都在三角形内部,并且三条中线相交于一点,这一点叫做三角形的重心.重心在三角形的内部.


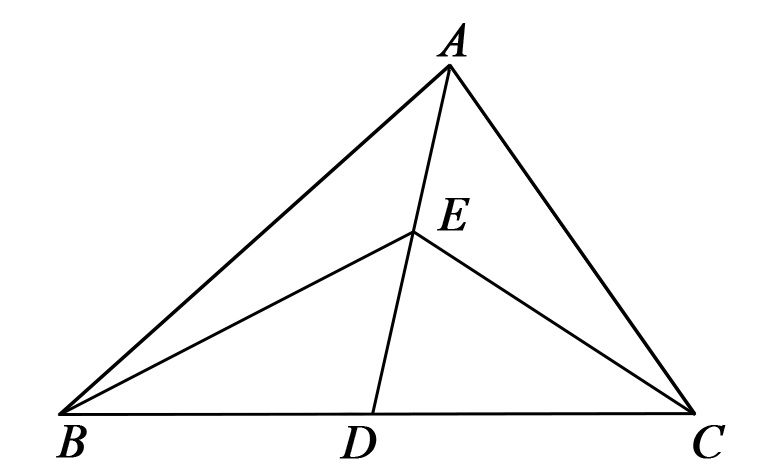
图9
A 2.5cm² B 2cm² C 1.5cm² D 1cm²
![]()
∵三角形的中线将三角形分成2个面积相等的三角形, AD是△ABC的中线, ∴S△ABD=S△ACD=1/2S△ABC=1/2×4=2(cm²). ∵E是AD的中点, ∴BE和CE分别是△ABD和△ACD的中线. ∴S△BDE=1/2S△ABD=1/2×2=1(cm²), S△CDE=1/2S△ACD=1/2×2=1(cm²). ∴S△BEC=S△BDE+S△CDE=1+1=2(cm²). 故选B. |




