图1
相信你学习了今天的知识,一定能解决这个问题.
![]()
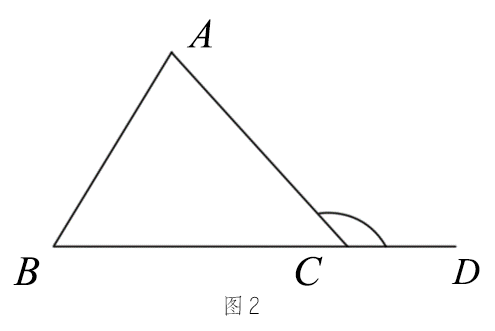
三角形外角的定义:三角形的一边与另一边的延长线组成的角, 叫做三角形的外角.
![]()
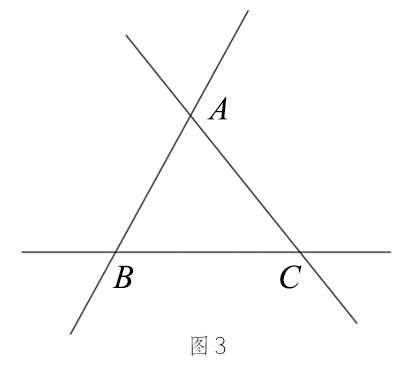
如图3,向两个方向延长三角形的各边,可以画出一个三角形的所有外角.
![]()
一个三角形有6个外角,其中有3个与另外3个分别相等. |
![]()
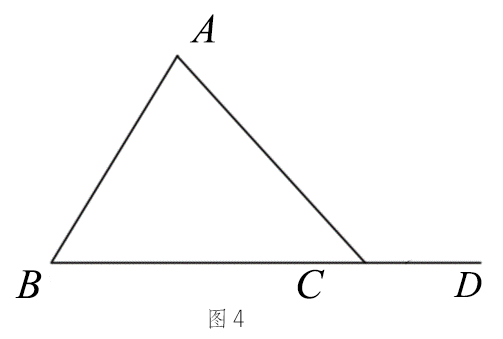
若∠A=70°,∠B=60°,则∠ACD = 130°; 若∠A=80°,∠B=40°,则∠ACD= 120°; 若∠A=m°,∠B=n°,则∠ACD= m°+ n°. 猜想:三角形的外角等于与它不相邻的两个内角的和. |
已知:如图5,∠ACD是△ABC的一个外角求证:∠ACD=∠A+∠B. |

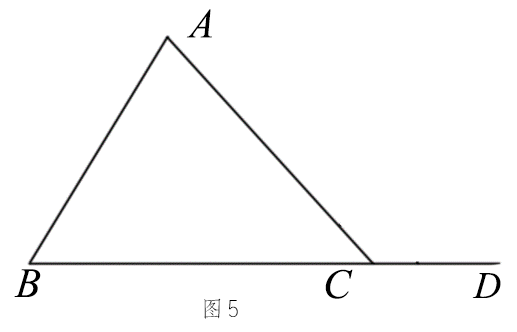 ∵∠A+∠B+∠ACB=180°, ∴∠ACB=180°-(∠A+∠B). ∵∠ACB+∠ACD=180°, ∴∠ACB=180°-∠ACD. ∴∠ACD=∠A+∠B. |
![]()
三角形的外角等于与它不相邻的两个内角的和. |
现在我们就可以用这个知识来解决课前提出的问题了.
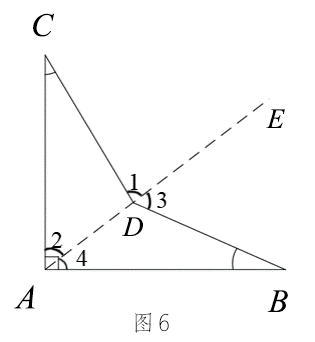
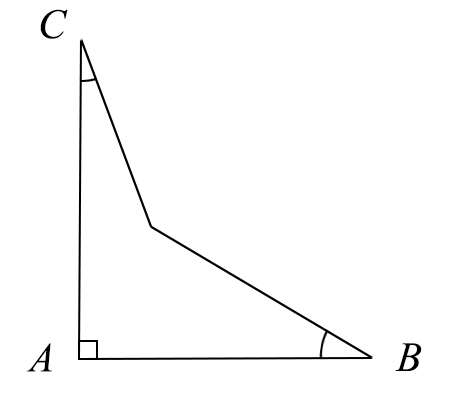
∵∠1=∠2+∠C ∠3=∠4+∠B ∴∠BDC=∠1+∠3 =(∠2+∠4)+∠B+∠C =∠BAC+∠B+∠C =90°+30°+20° =140°. 而量得∠BDC=142° , ∴零件不合格. |
![]()

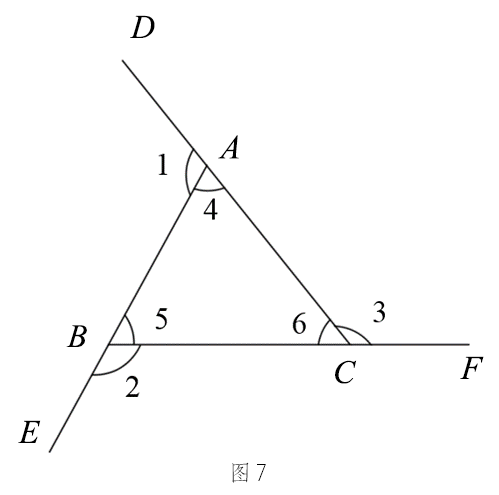
由三角形的一个外角等于与它不相邻的 两个内角的和,得: ∠1=∠5+∠6, ∠2=∠4+∠6, ∠3=∠4+∠5. ∴∠1+∠2+∠3=2(∠4+∠5+∠6). ∵∠4+∠5+∠6=180°, ∴∠1+∠2+∠3=2×180°=360°. |


∵∠1+∠4=180°, ∠2+∠5=180°, ∠3+∠6=180°. ∴(∠1+∠2+∠3)+(∠4+∠5+∠6)=540°. ∵∠4+∠5+∠6=180°, ∴∠1+∠2+∠3=540°-180°=360°. |