2.5    游程检验

游程检验的出发点是检验样本的独立性。几乎所有经典统计方法在理论上都要求样本是随机样本，即要求重复观察到的一组变量值在统计上相互独立。

参数统计很难考察这一问题，但从非参数的角度考察时，若数据出现趋势，周期性规律，就不能表示数据是独立的。这些问题可以转化为0－1序列或类型出现顺序的随机性问题。

Idea:掷硬币

Ø 以概率P得到正面（用1表示），以概率1-P得到反面（用0表示）------Bernoulli试验

Ø 如果试验是随机的，那么出现太多0和太多1连在一起是不太可能的，0或1频繁交替出现也是不太可能的。

Ø 比如：0000000 111111 0000 1111 00

Ø 连在一起的0或1称为游程（run），3个0游程，2个1游程，共5个游程，1的总个数m=10，0的总个数n=13，总试验次数为N=m+n=23

2.5.1 游程的概念

Ø 一个可以属性的总体，如按性别区分的人群，按产品是否合格区分的总体等等。

Ø 随机从中拍取一个样本，样本也可以分为两类；类型L和类型E。若凡属类型L的给以符号A，类型E的给以符号B，

Ø 当样本按某种顺序排列(如按抽取时间先后排列)时，一个或者一个以上相同符号连续出现的段，就被称作游程，

Ø 也就是说，游程是在一个两种类型的符号的有序排列中，相同符号连续出现的段。

例如，将某售票处排队等候购票的人按性别区分，男以A表示，女以B表示。按到来的时间先后观察序列为：AABABB。在这个序列中，AA为一个游程，连续出现两个A；B是一个游程，领先它的是符号A，跟随它的也是符号A；显然，A也是一个游程，BB也是一个游程。于是，在这个序列中，A的游程有2个，B的游程也有2个，序列共有4个游程。每一个游程所包含的符号的个数,称为游程的长度。如上面的序列中，有一个长度为2的A游程、一个长度为2的B游程，长度为1的A游程、B游程也各有1个。

    若序列随机，则游程的个数不能太多，也不能太少。游程长度也不应太长或太短。若游程个数过多，表示序列具有过度混合的倾向；若游程个数过少，表示序列具有成群聚集的倾向。这就是根据游程个数的游程检验出发点。

2.5.2 游程检验

1.假设：随机抽取的一个样本，其观察值按某种顺序排列，如果研究所关心的问题是：被有序排列的两种类型符号是否随机排列，则可以建立双侧备择．假设组为

Ø H0：序列是随机的

Ø H1：序列不是随机的

如果关心的是序列是否具有某种倾向，则应建立单侧备择，假设组为

Ø H0：序列是随机的

Ø H1: 序列具有混合的倾向

Ø H0：序列是随机的

Ø H1: 序列具有成群的倾向 

为了对假没作出判定，被收集的样本数据仅需定类尺度测量，但要求进行有意义的排序，按一定次序排列的样本观察值能够被变换为两种类型的符号。如某售票处按到来的先后顺序排队购票的人，按性别分别记作A、B两种类型的符号，可以得到一个序列：AABABB。第一种类型的符号数目记作m，第二种记作n，N =m+n。

2、检验统计量

在H0为真的情况下，两种类型符号出现的可能性相等，其在序列中是交互的。相对于一定的n1和n0，序列游程的总数应在一个范围内。若游程的总数过少，表明某一游程的长度过长，意味着有较多的同一符号相连，序列存在成群的倾向；若游程总数过多，表明游程长度很短，意味着两个符号频繁交替，序列具有混合的倾向。因此，无论游程的总数过多或过少，都表明序列不是随机的。 

Ø 根据两种类型符号的变化，选择的检验统计量为

Ø U＝游程的总数目

Ø 游程总数目U的抽样分布在附表VIII中（m+n<=20，或m<=n<=12）。

Ø 通常记m<=n，

Ø 当n＝足够大，则

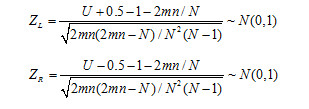
Z为负值时，右尾一般要“－0.5”。

3.确定P值
若p相对于给定的显著性水平小，则数据不支持H0；若足够大，则不拒绝H0。下表是判定的指导表。

应用之一：检验两个总体的位置参数是否相同

应用之二：检验单样本的随机性

应用之三：检验周期发生时间