第三节 跟驰理论

跟驰理论研究的一个主要目的是试图通过观察各个车辆逐一跟驰的方式来了解单车道交通流的特性。这种特性的研究可用来描述交通流的稳定性，加速干扰以及干扰的传播；检验在高速公路专用车道上运行的公共汽车车队的特性；检验管理技术和通信技术，以便预测短途车辆对市区交通流的影响，使尾撞事故减到最低限度

一、车辆跟驰特性分析

跟驰理论就是研究这种运行状态车队的行驶特性：

非自由状态行驶的车队有以下三个特性：

1．制约性 在一队汽车中，驾驶员总不愿意落后，而是紧随前车前进。这就是“紧随要求”。同时，后车的车速不能长时间的大于前车车速，只能在前车车速附近摆动，否则会发生碰撞。这是“车速条件”。此外，前后车之间必须保持一个安全距离，在前车制动后，两车之间有足够的距离，从而有足够的时间供后车驾驶员作出反应，采取制动措施。这是“间距条件”。

紧随要求、车速条件和间距条件构成了一队汽车跟驰行驶的制约性。即前车车速制约着后车车速和两车间距。

2．延迟性 从跟驰车队的制约性可知，前车改变运行状态后，后车也要改变。但前后车运行状态的改变不是同步的，后车运行状态的改变滞后于前车。因为驾驶员对前车运行状态的改变要有一个反应过程，需要反应时间。假设反应时间为T，那么前车在t时刻的动作，后车在（t+T）时刻才能作出相应的动作。这就是延迟性。

3．传递性  由制约性可知，第一辆车的运行状态制约着第2辆车的运行状态，第2辆又制约着第3辆，……，第n辆制约着第n+1辆。一旦第一辆车改变运行状态，它的效应将会一辆接一辆地向后传递，直至车队的最后一辆。这就是传递性。而这种运行状态的传递又具有延迟性。这种具有延迟性的向后传递的信息不是平滑连续的，而是像脉冲一样间断连续的。

第四节流体力学模拟理论

该理论运用流体力学的基本原理，模拟流体的连续性方程，建立车流的连续性方程。通过分析车流波的传播速度，以寻求车流流量和密度、速度之间的关系。因此，该理论又可称为车流波动理论。

一、车流连续性方程的建立

假设车流顺次通过断面Ⅰ和Ⅱ的时间间隔为dt，两断面的间距为dx，同时，车流在断面Ⅰ的流入量为 q，密度为 k。车流在断面Ⅱ的流出量为（q＋ dq），密度为（k-dk）。dk取负号表示在拥挤状态，车流密度随车流量的增加而减少。

根据质量守恒定律：

流入量一流出量=数量上的变化

二、车流中的波

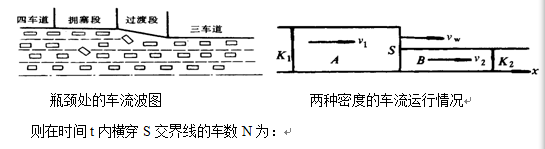
1．基本方程  假设一直线路段被垂直线S分割为A、B两段。A段的车流速度为v₁，密度为k₁；B段的车流速度为v₂，密度为k₂；S处的速度为v_w，假定沿路线按照所画的箭头X正方向运行，速度为正，反之为负，并且：v₁一在A区车辆的区间平均车速；v₂一在B区车辆的区间平均车速。