第一课时 交通流统计分布特性(课件)
上一节
下一节
第一节 交通流的统计分布特性
一、泊松分布
1、基本公式
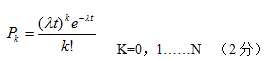
式中:P(x)——在计数周期t内到达x车辆的概率;
t——每个计数周期的持续时间,S;
入——单位时间平均到达率,veh/s;
m——在t时间间隔内平均到达的车辆数,m=入t
e——自然对数的底,取值为 2.71828。
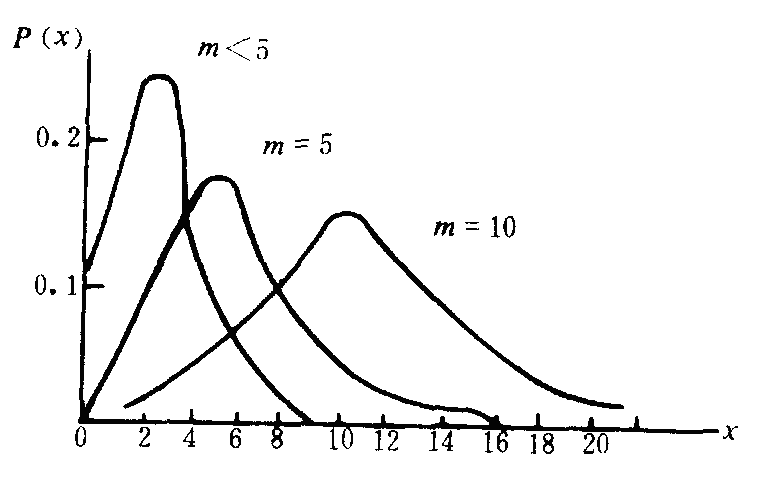
图8-5泊松分布

5.适用条件
适用于交通流量小,驾驶员随意选择车速,车辆到达是随机的,判据为:
均值与方差相等
二、二项分布
1.基本公式
交通流为拥挤车流,观测周期t内到达x辆车的概率服从二项分布,公式为:

2.递推公式

三、计算示例
例8-1在平均交通量为120辆/h的道路上,已知交通流到达服合泊松分布,求30s内无车到达、有1辆、有2辆、有3辆、有四辆及电辆以上车通过的概率。
解:已知观测周期t=30s

例8-2设60辆汽车随机分布在4km长的道路上,求任意400m路段上有4辆车的概率及4辆以上车的概率。
例8-3一交叉口.设置了专供左转的信号相,经研究指出:来车符合二项分布。每一周期内平均到达20辆车,有25要的车辆左转但无右转。求:
①到达三辆车中有一辆左转的概率。
②某一周期不使用左转信号相的概率。


