实验

1784年至1785年间，法国物理学家查尔斯·库仑通过扭秤实验验证了这一定律。扭秤的结构如右图所示：在细金属丝下悬挂一根秤杆，它的一端有一小球A，另一端有平衡体P，在A旁还置有另一与它一样大小的固定小球B。为了研究带电体之间的作用力，先使A、B各带一定的电荷，这时秤杆会因A端受力而偏转。转动悬丝上端的悬钮，使小球回到原来位置。这时悬丝的扭力矩等于施于小球A上电力的力矩。如果悬丝的扭力矩与扭转角度之间的关系已事先校准、标定，则由旋钮上指针转过的角度读数和已知的秤杆长度，可以得知在此距离下A、B之间的作用力，并且通过悬丝扭转的角度可以比较力的大小。

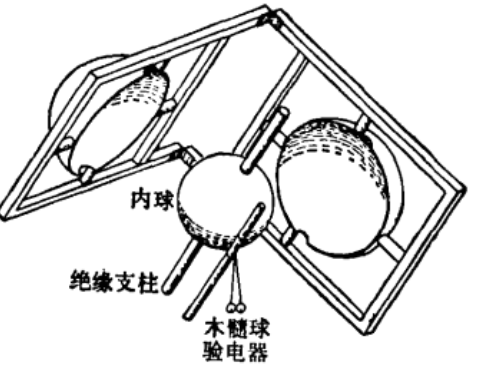
1773年，卡文迪许用两个同心金属球壳做实验，如右图，外球壳由两个半圆装配而成，两半球合起来正好把内球封在其中。通过一根导线将内外球连在一起，外球壳带点后，取走导线，打开外壳，用木髓球验电器试验有没有带电，结果发现木髓球验电器没有指示，内球不带电荷。根据这个实验，卡文迪许确定指数偏差 ，比罗宾逊1769年得出的0.06更精确。

1873年，麦克斯韦和麦克阿利斯特改进了卡文迪许的这个实验。麦克斯韦亲自设计实验装置和实验方法，并推算了实验的处理公式。他们将F表示为 ，其中q不超过 。这个实验做得十分精确，以致直到1936年未曾有人超过他们。

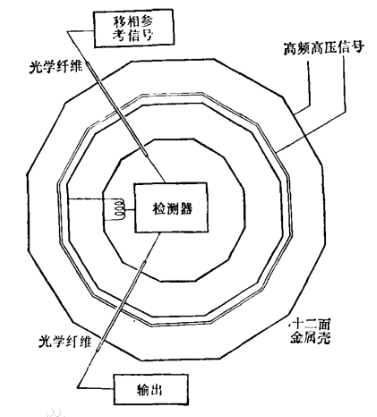1971年，美国Wesleyan大学的Edwin R．Williams，James E．Faller及Henry A．Hill用现代测试手段，将平方反比定律的指数偏差又延伸了好几个数量级。在此之前已有好几起实验结果，不断地刷新纪录。Williams等人采用高频高压信号、锁定放大器和光学纤维传输来保证实验条件，但基本方法和设计思想跟卡文迪许和麦克斯韦是一脉相承的。

左图是简单示意图，他们用五个同心金属壳，而不是两个，采用十二面体形，而不是球形。峰值为10千伏的4兆赫高频高压信号加在最外面两层金属壳上，检测器接到最里面的两层，检验是否接收到信号。 

他们根据麦克斯韦的公式如上图所示，得到的平方反比定律的指数偏差。