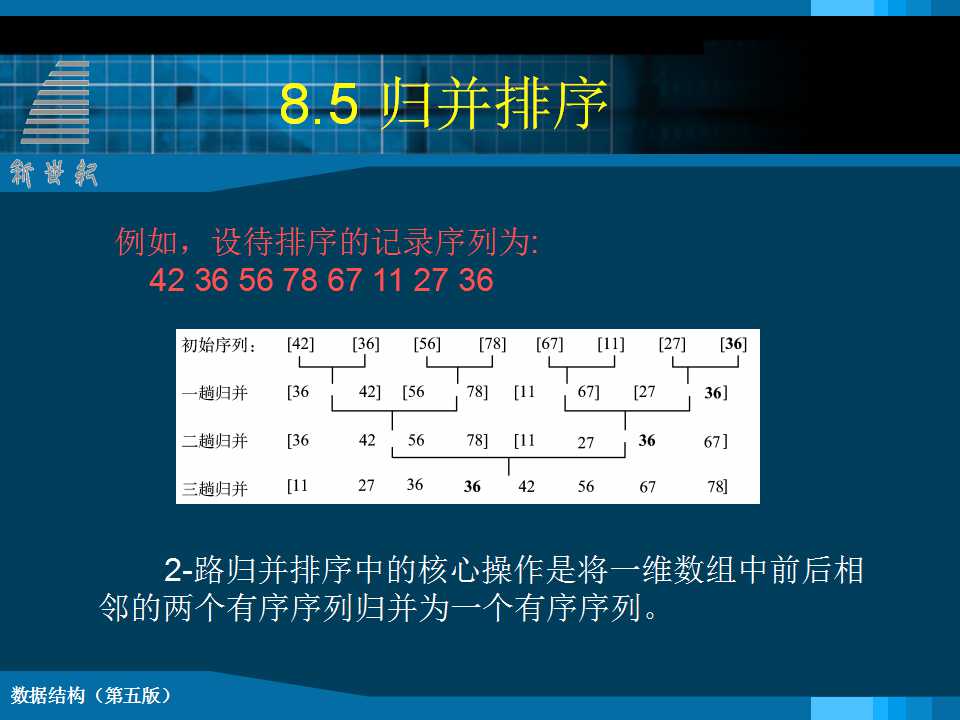
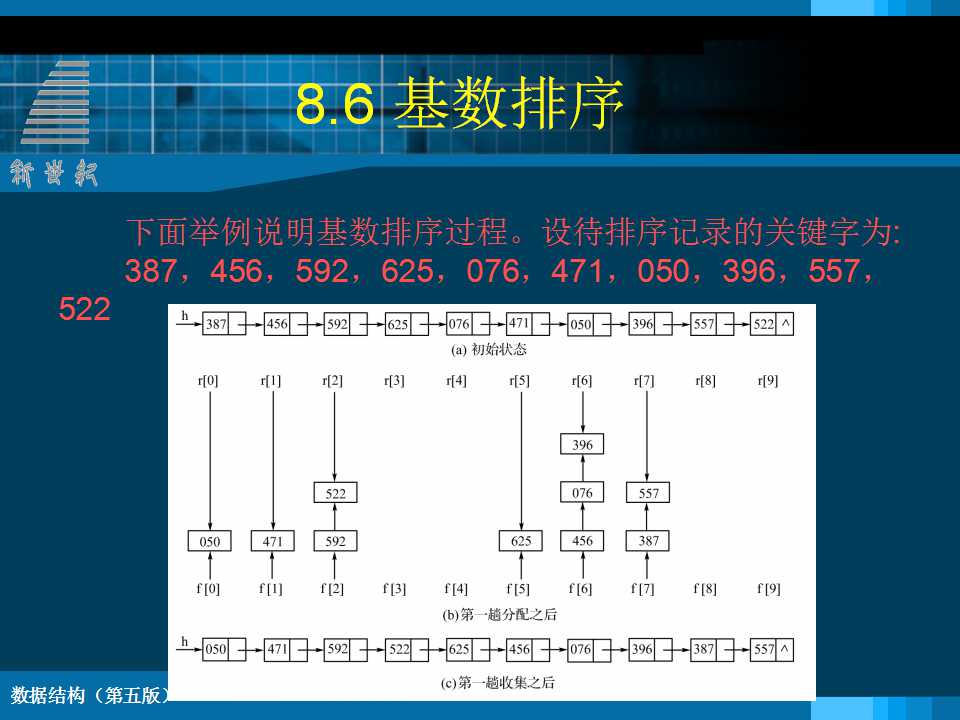
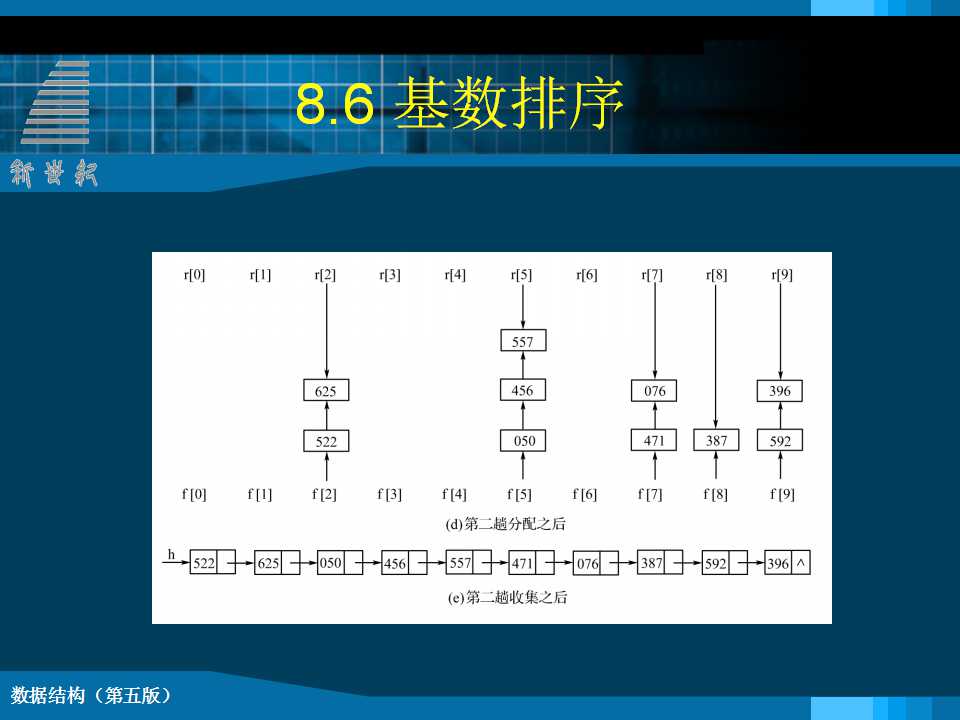
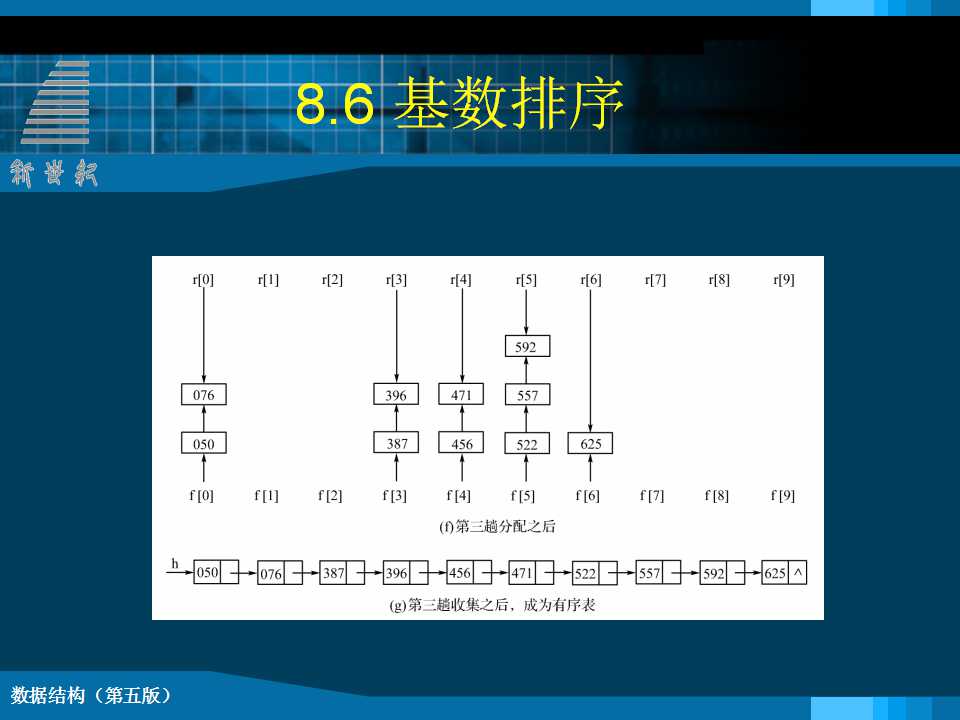
1 堆的定义

n个元素的序列(k1,k2,……kn),当且仅当满足下列关系时,称之为堆。

若将此序列对应的一维数组看成是一个完全二叉树,则ki为二叉树的根结点,k2i和k2i+1分别为ki的“左子树根”和“右子树根”。

堆排序

将无序序列建成一个堆,得到关键字最小(或最大)的记录;输出堆顶的最小(大)值后,使剩余的n-1个元素重又建成一个堆,则可得到n个元素的次小值;重复执行,得到一个有序序列的过程。

堆排序需解决的两个问题:

如何由一个无序序列建成一个堆？(初始建堆)

如何在输出堆顶元素之后,调整剩余元素,使之成为一个新的堆？

void HeapAdjust (SqList &H, int s, int m)

{// 已知H.r[s..m]中记录的关键字除H.r[s].key之外均满足//堆的定义, 本函数调整H.r[s]的关键字,使H.r[s..m]成为//一个大顶堆(对其中记录的关键字而言)

rc = H.r[s];　　　　　　　　  // 暂存根结点的记录

for(j=2*s;j<=m;j*=2 )

  { // 沿关键字较大的孩子结点向下筛选
if ( j<m && H.r[j].key<H.r[j+1].key )  ++j; 　　　　　　　　　　　             //j为关键字较大的孩子记录下标
if (! (rc.key<H.r[j].key )) break;
                         // 不需要调整,跳出循环
H.r[s] = H.r[j]; s = j;  // 将大关键字记录往上调
}// for

H.r[s] = rc; 　　　　　　    // 回移筛选下来的记录

} // HeapAdjust

void HeapSort ( SqList &H )

{// 对顺序表H进行堆排序

for ( i=H.length/2; i>0; --i )
// 将 H.r[1..H.length] 建成大顶堆
HeapAdjust ( H, i, H.length );

for ( i=H.length; i>1; --i )

  {
H.r[1] « H.r[i]; // 将堆顶记录和当前未经排
// 序的子序列H.r[1..i]中最
// 后一个记录互相交换
HeapAdjust(H, 1, i-1);//将H.r[1..i-1]重新调整为
// 大顶堆
}//for

} // HeapSort

2 归并排序

归并

将两个或两个以上的有序表组合成一个新的有序表。

void Merge(RcdType SR[],RcdType &TR[],int i,int m,int n)

{// 将有序的SR[i..m]和SR[m+1..n]归并为有序的TR[i..n]

for (j=m+1, k=i; i<=m && j<=n; ++k){
// 将SR中记录按关键字从小到大地复制到TR中
if ( LQ(SR[i].key, SR[j].key)) TR[k] = SR[i++];
else TR[k] = SR[j++];
}

while(i<=m) TR[k++] = SR[i++];//将剩余的SR[i..m]复制到TR

while(j<=n) TR[k++] = SR[j++];//将剩余的SR[j..n]复制到TR

} // Merge