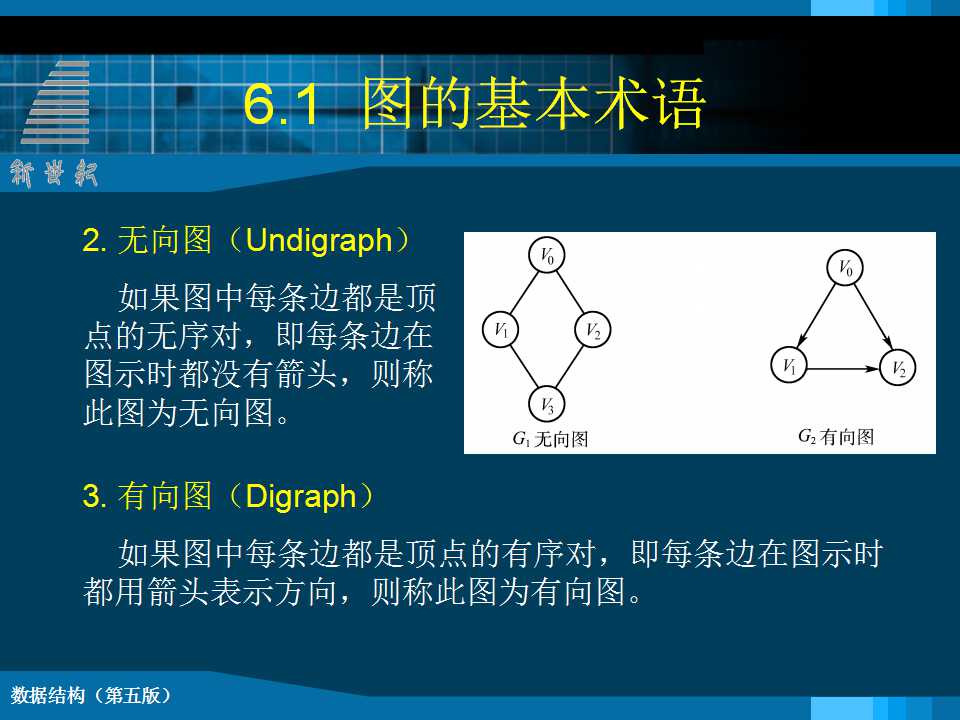
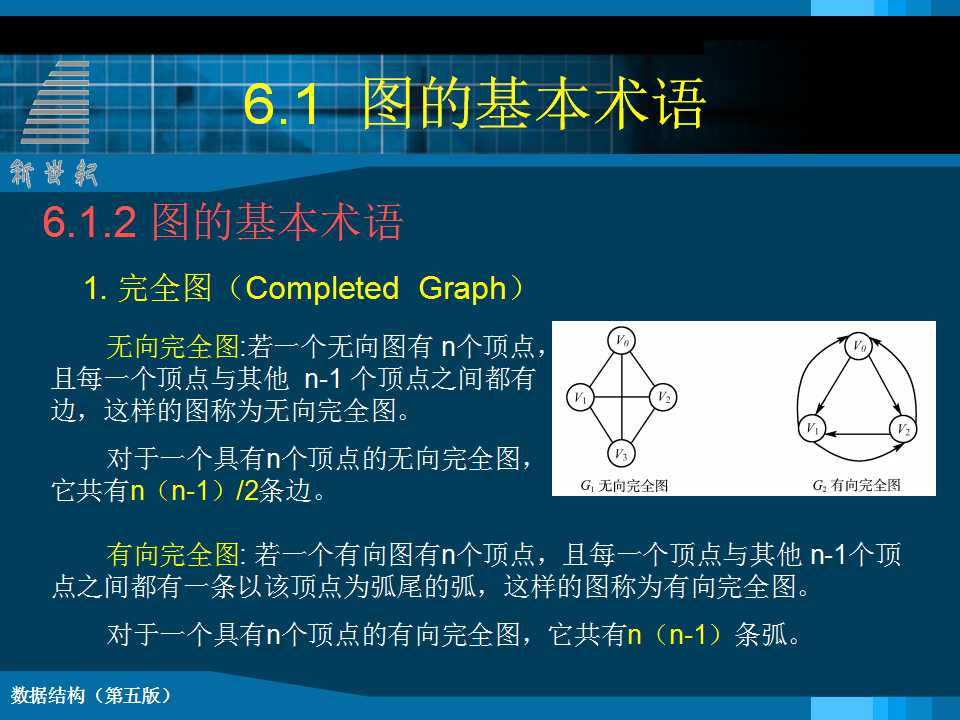
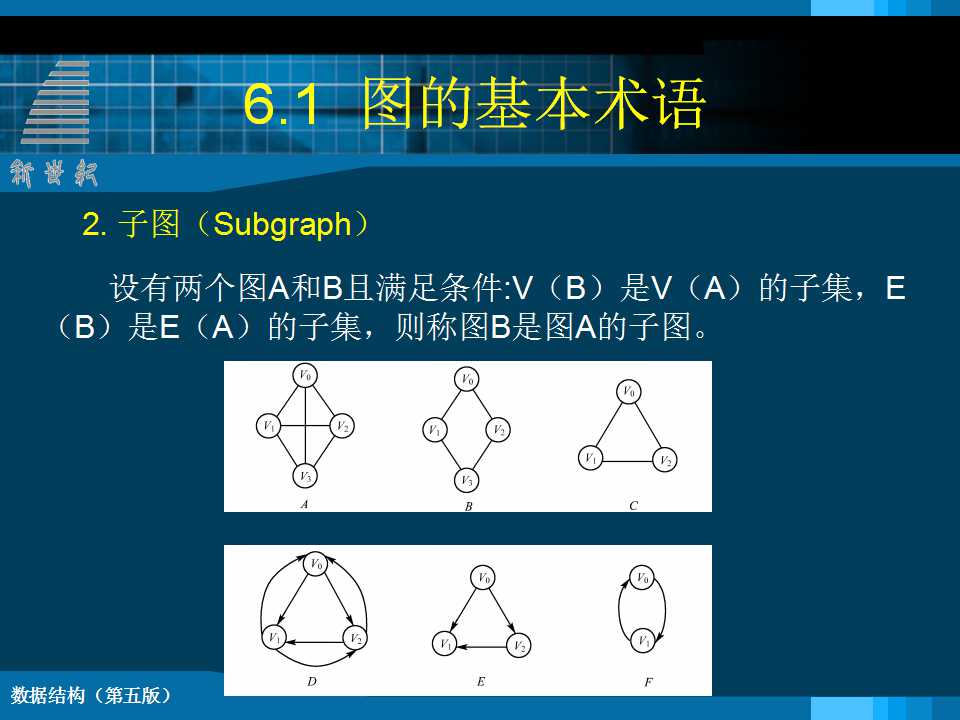
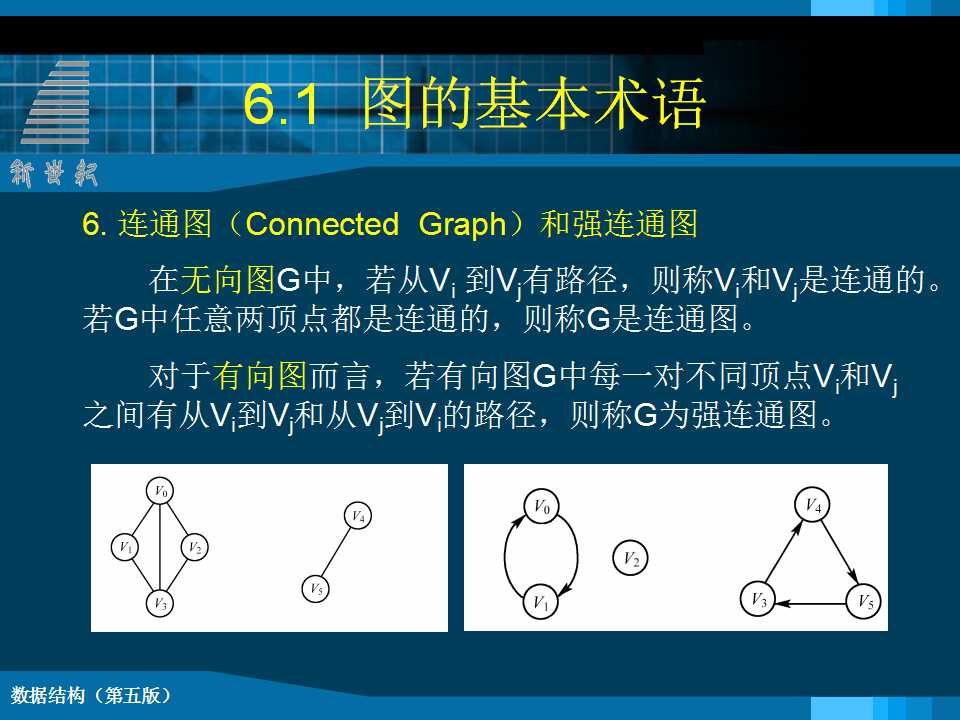
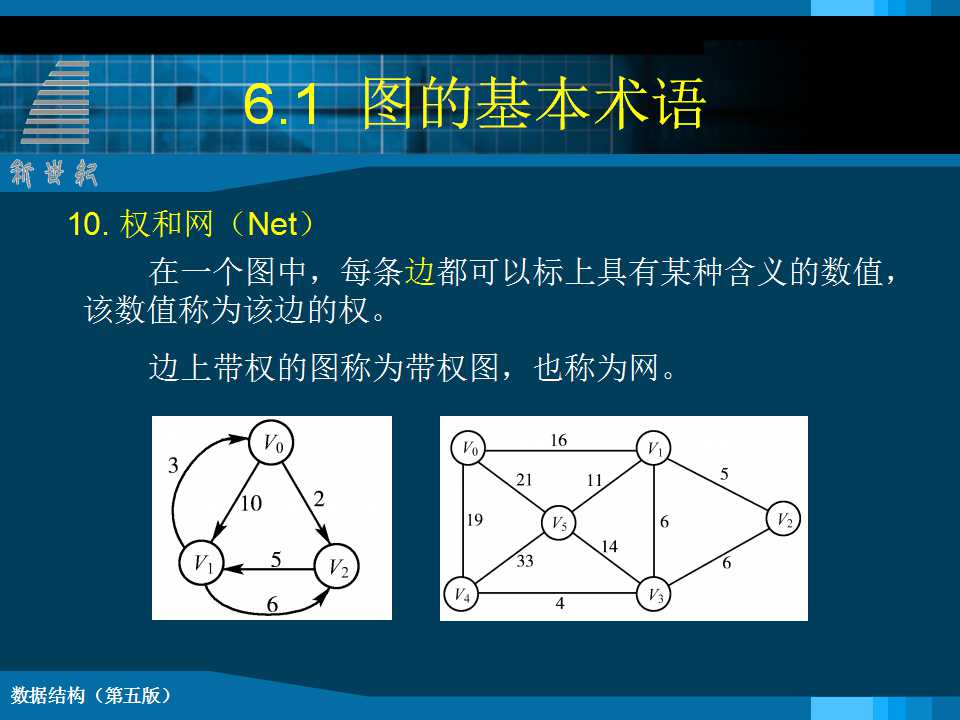
一图的结构定义:

图是由一个顶点集 V 和一个弧集 R构成的数据结构。

        Graph = (V , R )

其中，VR＝{<v,w>| v,w∈V 且 P(v,w)}

   <v,w>表示从 v 到 w 的一条弧，并称 v 为弧尾，w 为弧头。

 谓词 P(v,w) 定义了弧 <v,w>的意义或信息

6.1.2  有关图的常用术语

1．顶点的度、入度、出度 

无向图中，若顶点vi和vj之间有一条边（vi，vj）存在，则表明顶点vi和vj互为邻接点，简称vi与vj相邻接。所谓顶点vi的“度”，是指与它相邻接的顶点的个数，记为D(vi)。

2邻接点

对于无向图G＝(V，{E})，如果边（v1，v2）∈E，则称顶点v1，v2互为邻接点，即v1，v2相邻接。边（v1，v2）依附于顶点v1和v2 ，或者说边（v1，v2）与顶点v1和v2相关联。 

3．路径、路径长度

在无向图G中，所谓从顶点vi到顶点vj的一条“路径”，是指在顶点vi与顶点vj之间存在有一个边的序列：

（vi, vi1），（vi1, vi2），…，（vim,vj）

    其中顶点vi、vi1、vi2、…、vim、vj属于G的顶点集合V，边（vi, vi1）、（vi1,vi2）、…、（vim, vj）属于G的边的集合E。

4．简单路径、回路

在图G＝(V，E)中，如果有结点序列：

 Vp，Vi1，Vi2…，Vin，Vq ，使得{ (Vp ，Vi1)，(Vi1 ， Vi2)，…，(Vin，Vq) }∈E（若对有向图，则存在一系列弧）则称从结点Vp到结点Vq存在一条路径，路径长度就为这条路径上的边数。如果一条路径上的结点除Vp和Vq可以相同外，其它结点都不相同，则称此路径为一简单路径。

5．无向完全图、有向完全图

若一个有n个顶点的无向图，拥有n(n−1)/2条边，那么就称该图为“无向完全图”。对于一个无向完全图来说，它的每个不同顶点对之间，都存在有一条边。 若一个有n个顶点的有向图，拥有n(n−1)条弧，那么就称该图为“有向完全图”。

对于一个有向完全图来说，它的每个不同顶点对之间，都存在有两条弧。

6．子图

已知两个图G=（V，E），G′=（V′，E′）。若有V′是V的子集，E′是E的子集，且E′中的边（或弧）都依附于V′中的顶点，那么就称G′是G的一个“子图”。

7．连通、连通图、连通分量

在无向图中，若从顶点vi到顶点vj之间有路径存在，则称vi与vj是“连通”的。如果无向图G中任意一对顶点之间都是连通的，则称该图G为“连通图”，否则是非连通图。

8．边的权、网络

有时，可以给图的边或弧依附上某种数值，这种与图的边或弧相关的数值被称为“权”。边或弧上带有权的图称为“网图”或“网络”。

9.生成树：n个顶点的连通图的生成树是一个极小连通子图，它包含连通图的全部顶点及n-1条边，使所有顶点都连通但不构成回路。生成树具有两个特点：

n 1）n个顶点的生成树包含n-1条边；

n 2）如果在生成树中任意增加一条边，则有一条回路。

6.2.1 邻接矩阵

所谓“邻接矩阵”，是表示顶点之间相邻关系的矩阵，是指一种存储结构的组合。 

用一个一维数组存储图中顶点的数据信息；用一个二维数组（即矩阵）存储图中各顶点间的邻接关系。通常，简略地只是把这个组合中的二维数组称作是图的“邻接矩阵”。

6.2.2 邻接表

邻接表表示图是由两部分构成，即顶点数据表和表示数据关系的边（弧）构成的表：

  ⑴ 顶点数据表：由所有顶点数据信息以顺序结构的向量表形式存储，一个表目对应于图的一个结点，每个表目包括两个部分，其一是表示数据的，可以是数据或指向结点数据的指针（data）；另一个是表示边（弧）的指针，该指针（firstarc）指向相邻的第一条边（弧），通过这个指针便可以随机访问相邻的任一顶点。

6.2.3十字链表

十字链表(Orthogonal List)是有向图的另一种链式存储结构。我们也可以把它看成是将有向图的邻接表和逆邻接表结合起来形成的一种链表。有向图中的每一条弧对应十字链表中的一个弧结点，同时有向图中的每个顶点在十字链表中对应有一个结点，叫做顶点结点。

6.2.4邻接多重表