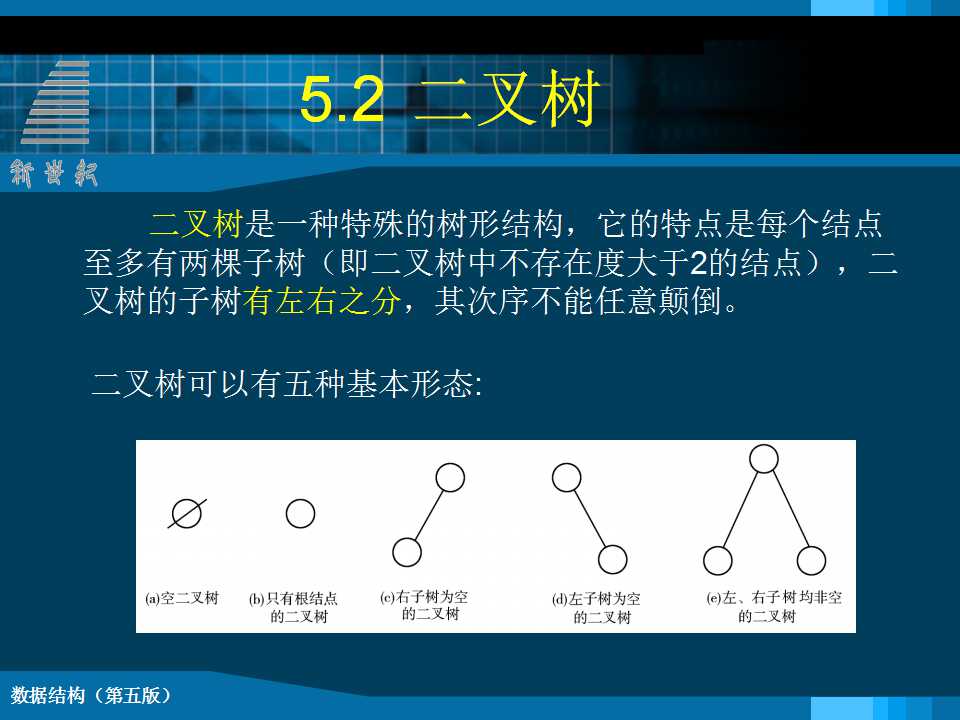
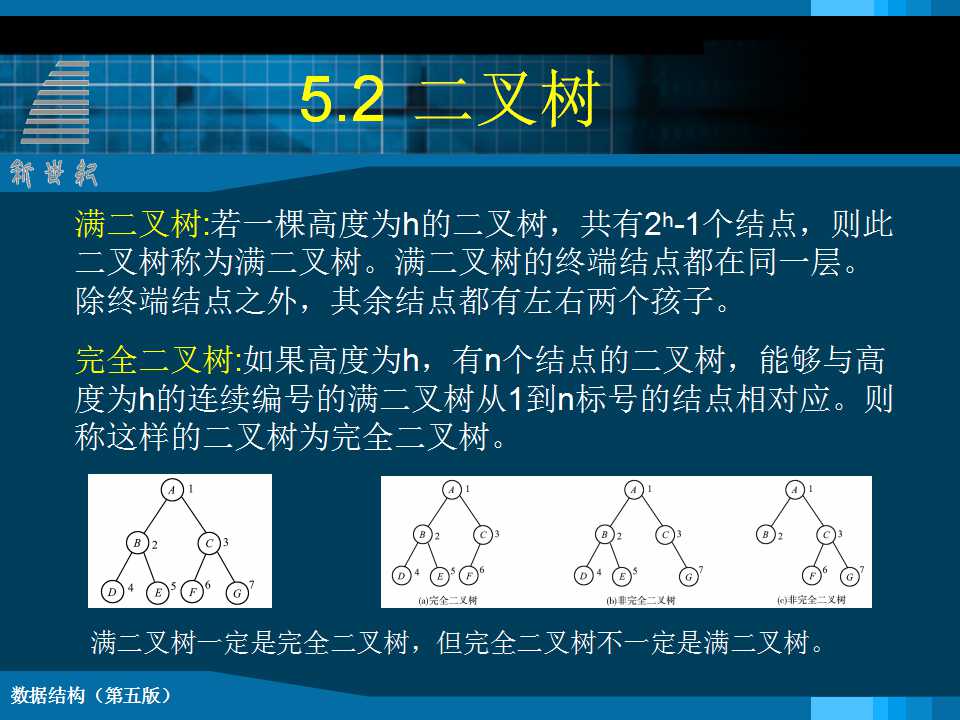
6.2   二  叉 树 

6.2.1   二叉树的定义

二叉树（Binary Tree）：和树不同的树型结构

（1） 每个结点的度都不大于2；

（2） 有序树：每个结点的孩子结点次序不能任意颠倒     

二叉树的重要特性

性质1: 在二叉树的第i层上至多有2i-1个结点(i≥1) 

性质2: 深度为k的二叉树至多有2k-1个结点（k≥1）

性质3: 对任意一棵二叉树T，若终端结点数为n0，而其度数为2的结点数为n2，则n0=n2+1

性质4：具有n个结点的完全二叉树的深度为  log2n  +1

性质5:  对于具有n个结点的完全二叉树， 如果按照从上到下和从左到右的顺序对二叉树中的所有结点从1开始顺序编号， 则对于任意的序号为i的结点有：

满二叉树： 深度为k且有2k-1个结点的二叉树。在满二叉树中，每层结点都是满的，即每层结点都具有最大结点数。 

完全二叉树： 深度为k，结点数为n的二叉树，如果其结点1~n的位置序号分别与满二叉树的结点1~n的位置序号一一对应，则为完全二叉树。 

6.3顺序存储结构 

链式存储结构

 对于任意的二叉树来说，每个结点只有两个孩子，一个双亲结点。我们可以设计每个结点至少包括三个域：数据域、 左孩子域和右孩子： 

6.3二叉树的遍历

先序遍历（DLR）操作过程：

若二叉树为空， 则空操作， 否则依次执行如下3个操作：

² 访问根结点；

² 按先序遍历左子树；

² 按先序遍历右子树。 

中序遍历（LDR）操作过程：

   若二叉树为空， 则空操作， 否则依次执行如下3个操作： 

² 按中序遍历左子树；

² 访问根结点；

² 按中序遍历右子树。

后序遍历（LRD）操作过程：

   若二叉树为空， 则空操作， 否则依次执行如下3个操作： 

² 按后序遍历左子树；

² 按后序遍历右子树；

² 访问根结点。 

VoidPreorder(BiTreeT, void( *visit)(TElemType& e))

{ // 先序遍历二叉树 

   if (T) {

      visit(T->data);            // 访问结点

      Preorder(T->lchild, visit); // 遍历左子树

      Preorder(T->rchild, visit);// 遍历右子树

   }

}

BiTNode *GoFarLeft(BiTree T, Stack *S){

   if (!T )  return NULL;

   while (T->lchild ){

      Push(S, T);

      T = T->lchild;

   }

   return T;

}

voidInorder_I(BiTreeT,void(*visit)                                  (TelemType& e)){

   Stack *S;

   t = GoFarLeft(T, S);  // 找到最左下的结点

   while(t){

      visit(t->data);

      if (t->rchild)

         t = GoFarLeft(t->rchild, S);

     else if ( !StackEmpty(S ))    // 栈不空时退栈

        t = Pop(S);

              else    t = NULL; // 栈空表明遍历结束

    } // while

}// Inorder_I