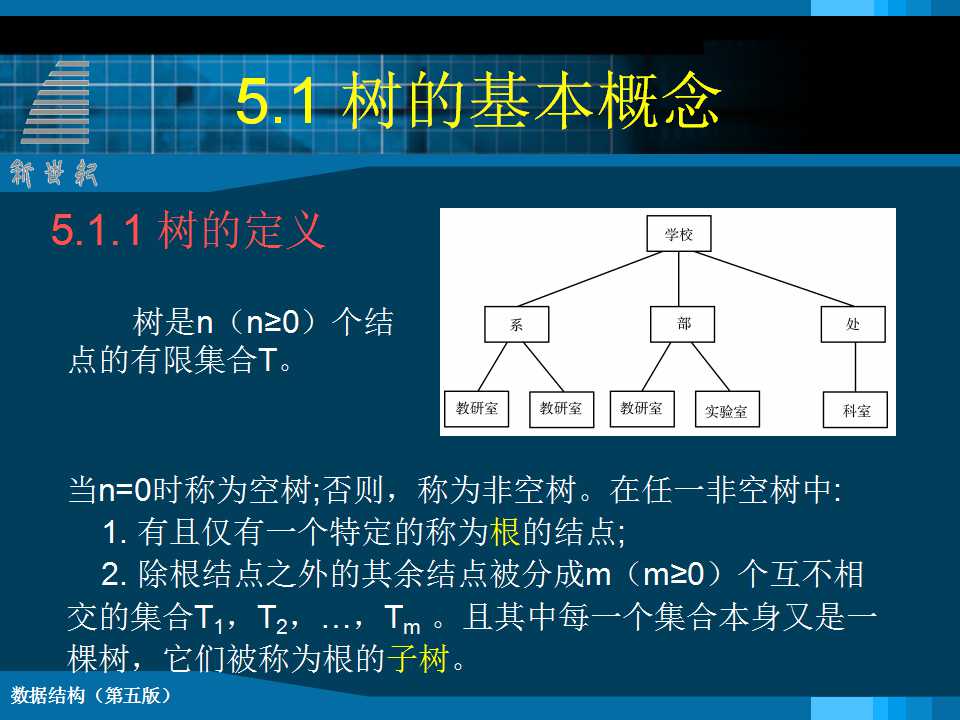
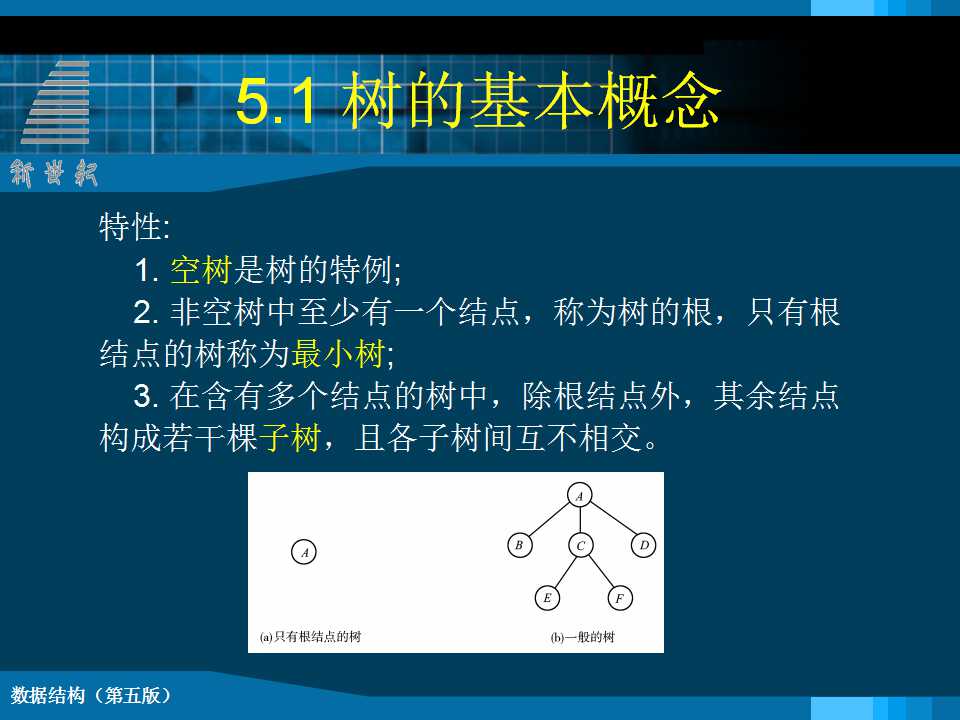
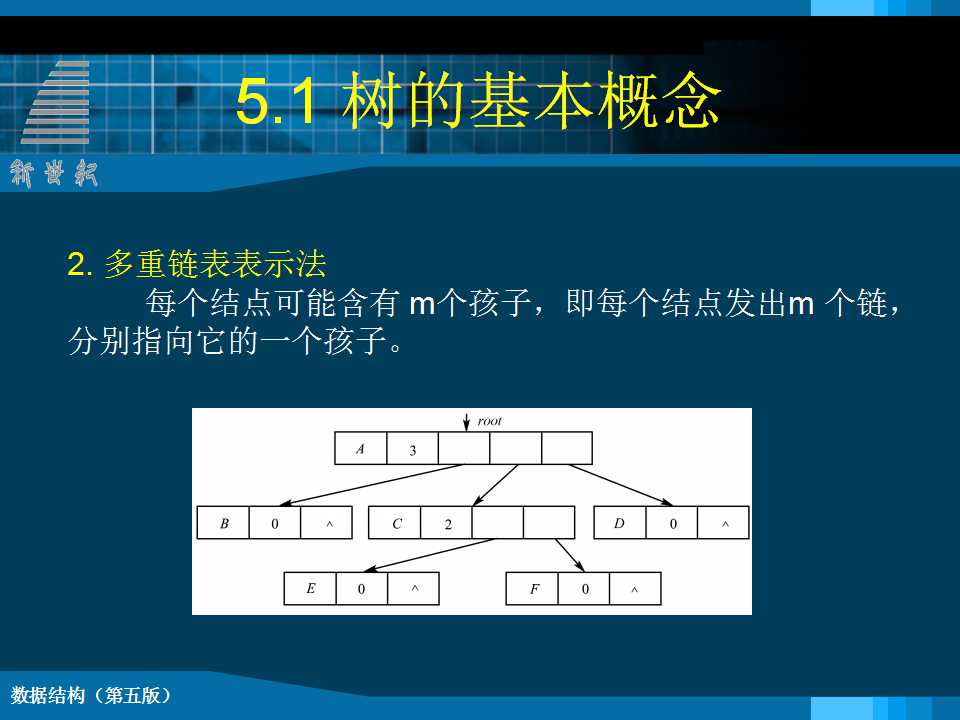
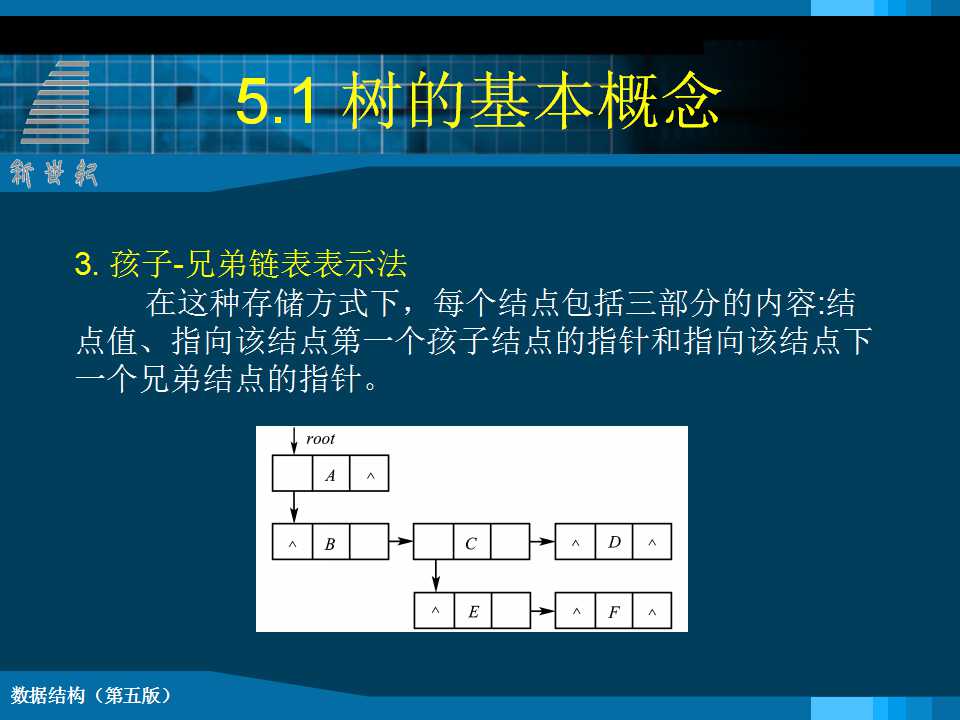
一定义

树（Tree）是n（n≥0）个结点的有限集合T。当n=0时，称为空树；当n>0时， 该集合满足如下条件：

 (1) 其中必有一个称为根（root）的特定结点，它没有直接前驱，但有零个或多个直接后继。

 (2) 其余n-1个结点可以划分成m（m≥0）个互不相交的有限集T1，T2，T3，…，Tm，其中Ti又是一棵树，称为根root的子树。 每棵子树的根结点有且仅有一个直接前驱，但有零个或多个直接后继。 

树的表示

u 树形表示法

u 集合图表示

u 凹入表表示

u 广义表表示

基  本  术  语

Ë 结点的度：结点所拥有的子树的个数。

Ë  树的度：树中各结点度的最大值。

Ë 叶子结点：度为0的结点，也称为终端结点。

Ë  分支结点：度不为0的结点，也称为非终端结点。

Ë 孩子、双亲：树中某结点子树的根结点称为这个结点的孩子结点，这个结点称为它孩子结点的双亲结点；

Ë  兄弟：具有同一个双亲的孩子结点互称为兄弟。 

Ë 祖先：从根到该结点所经分支上的所有结点。

Ë 子孙：以某结点为根的子树中的任一结点都称为该结点的子孙。

Ë 结点所在层数：根结点的层数为1，根的孩子为第二层；对其余任何结点，若某结点在第k层，则其子树的根在第k+1层。

Ë  树的深度：树中所有结点的最大层数，也称高度。

层序编号：将树中结点按照从上层到下层、同层从左到右的次序依次给他们编以从1开始的连续自然数。

森林：

是m（m≥0）棵互不相交的树的集合。树中每个结点，其子树的集合称为森林。

任何一棵非空树是一个二元组

       Tree = （root，F）

其中：root 被称为根结点，    F 被称为子树森林