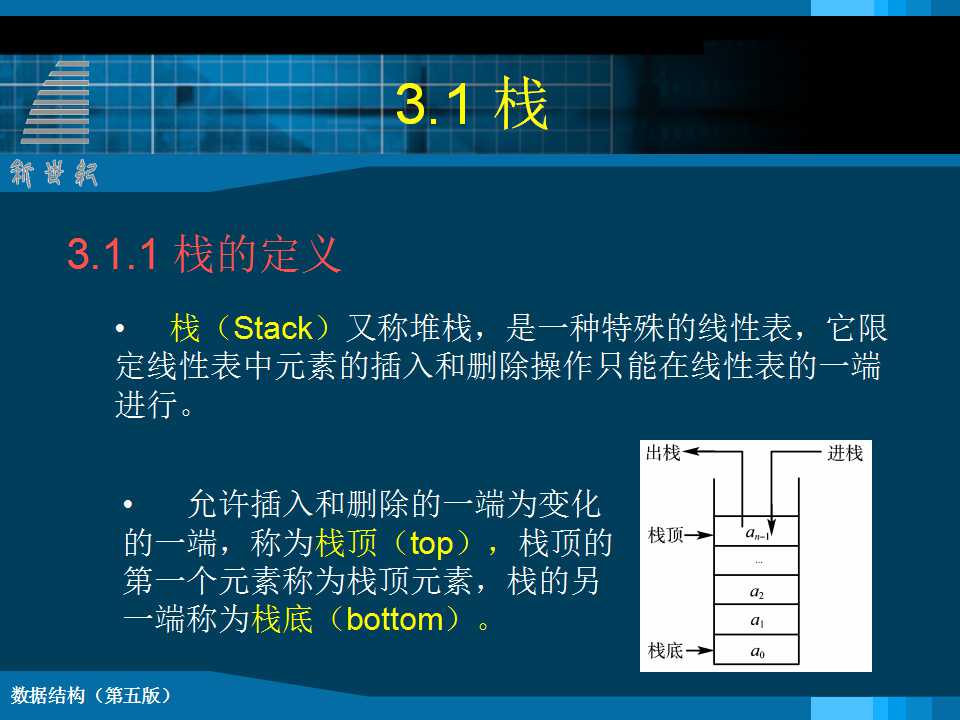
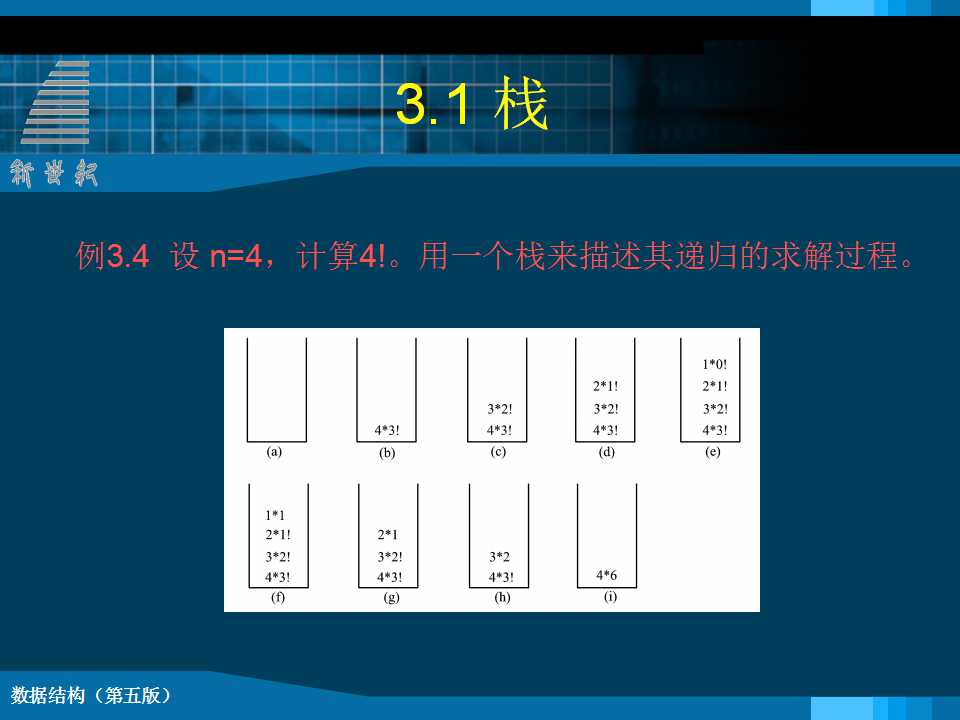
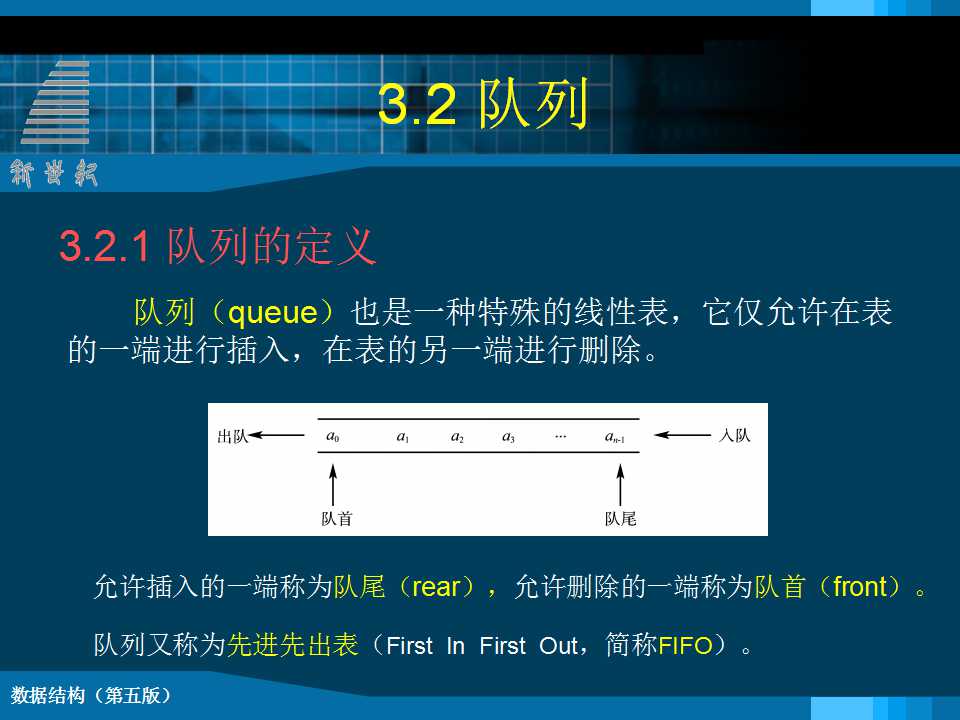
通常称，栈和队列是限定插入和删除只能在表的“端点”进行的线性表。

l 栈（Stack）是限定只能在表尾进行插入和删除操作的线性表。

l 表中进行插入、删除操作的一端称为栈顶（top）（表尾），栈顶保存的元素称为栈顶元素。相对的，表的另一端称为栈底（bottom）（表头）。

l 当栈中没有数据元素时称为空栈；向一个栈插入元素又称为进栈或入栈；从一个栈中删除元素又称为出栈或退栈。

l 栈和队列都是线性数据结构

n 栈：后进先出

n 队列：先进先出

3.1 栈的类型定义

ADT Stack {

      数据对象：

         D＝{ ai | ai ∈ElemSet, i=1,2,...,n,  n≥0 }

      数据关系：

         R1＝{ <ai-1, ai >| ai-1, ai∈D, i=2,...,n }

      基本操作：

} ADT Stack

栈的顺序存储实现

n 顺序栈是使用顺序存储结构实现的堆栈，即利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素。同时附设指针top指示栈顶元素在顺序栈中的位置。以top=0表示空栈。

n 根据数组操作的特性，选择数组下标大的一端，即线性表顺序存储的表尾来作为栈顶。

//----- 栈的顺序存储表示 -----

  #define  STACK_INIT_SIZE  100;

  #define  STACKINCREMENT   10;  

  typedef struct {

    SElemType  *base; //base为null表示栈不存在   

    SElemType  *top;  // top=base表示栈空

    int  stacksize;    

  } SqStack;

Status InitStack (SqStack &S)

{// 构造一个空栈S

  S.base=(ElemType*)malloc(STACK_INIT_SIZE*

                                         sizeof(ElemType));

   if (!S.base) exit (OVERFLOW); //存储分配失败

   S.top = S.base;

   S.stacksize = STACK_INIT_SIZE;

   return OK;

}

Status Push (SqStack &S, SElemType e) {

   if (S.top - S.base >= S.stacksize) {      S.base = (ElemType *) realloc ( S.base, (S.stacksize + STACKINCREMENT) * 

                                                   sizeof (ElemType));

       if (!S.base) exit (OVERFLOW);   

    S.top = S.base + S.stacksize;

       S.stacksize += STACKINCREMENT;

   }

   *S.top++ = e;

    return OK;

}

Status Pop (SqStack &S, SElemType &e) {

     if (S.top == S.base) return ERROR;

    e = *--S.top;

    return OK;

}

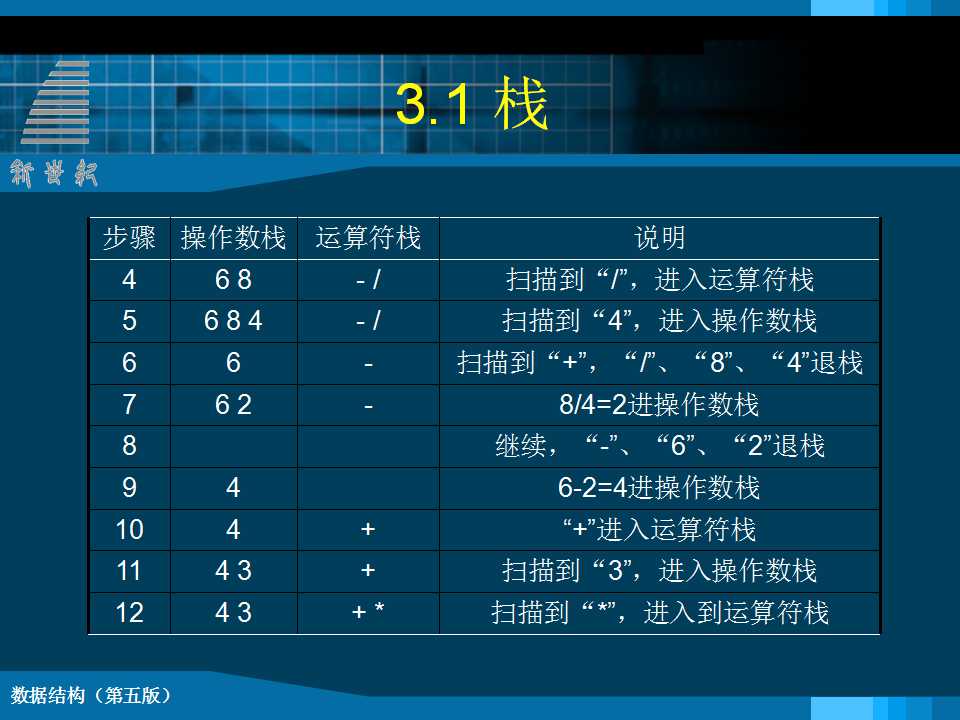
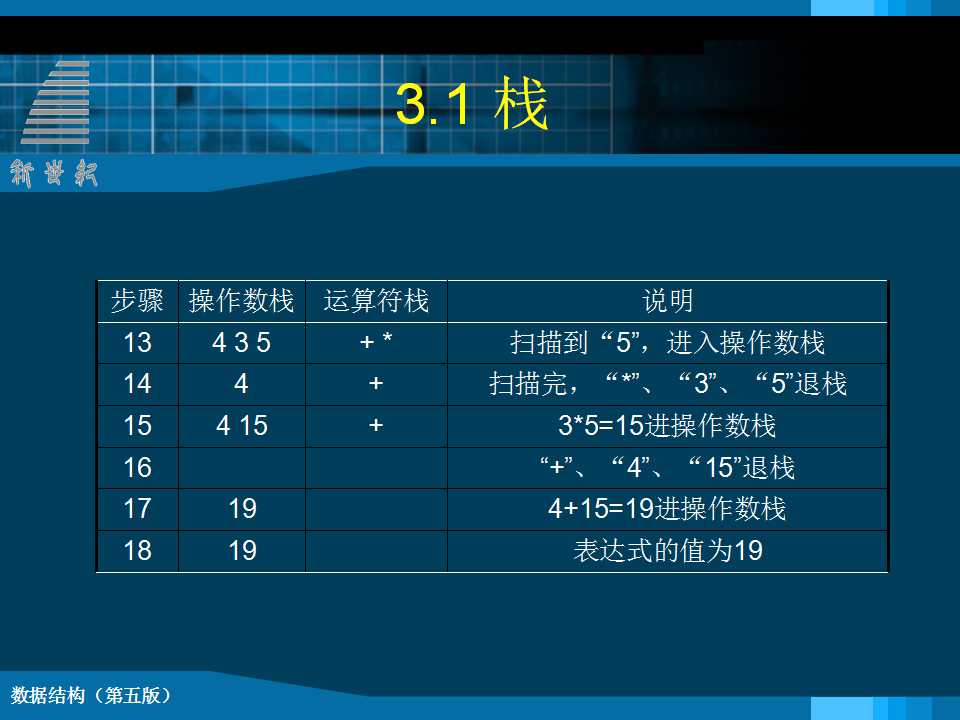
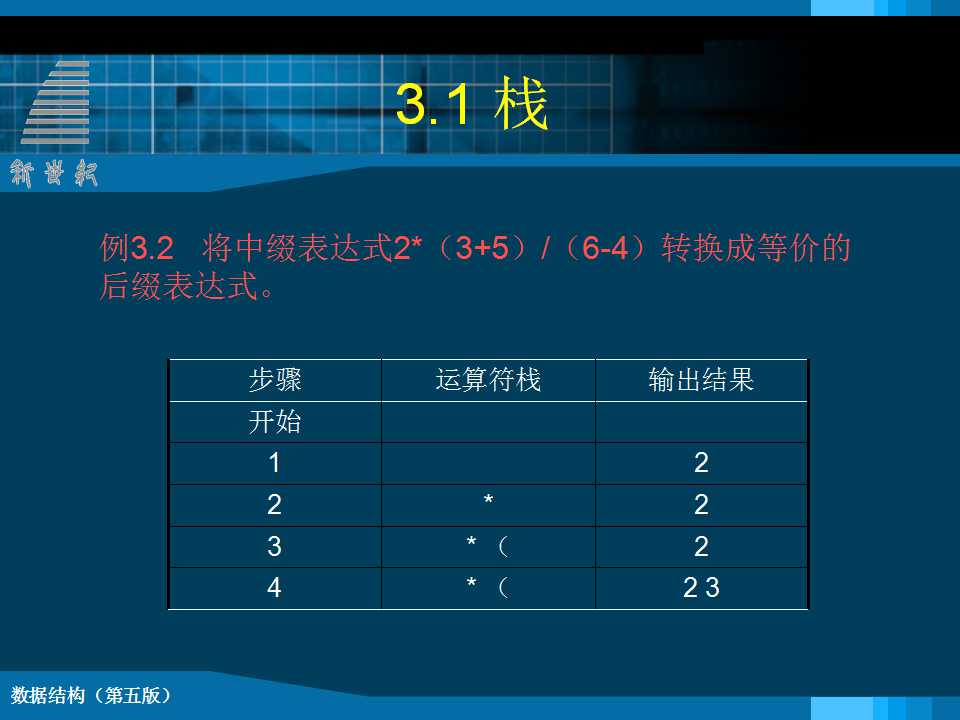
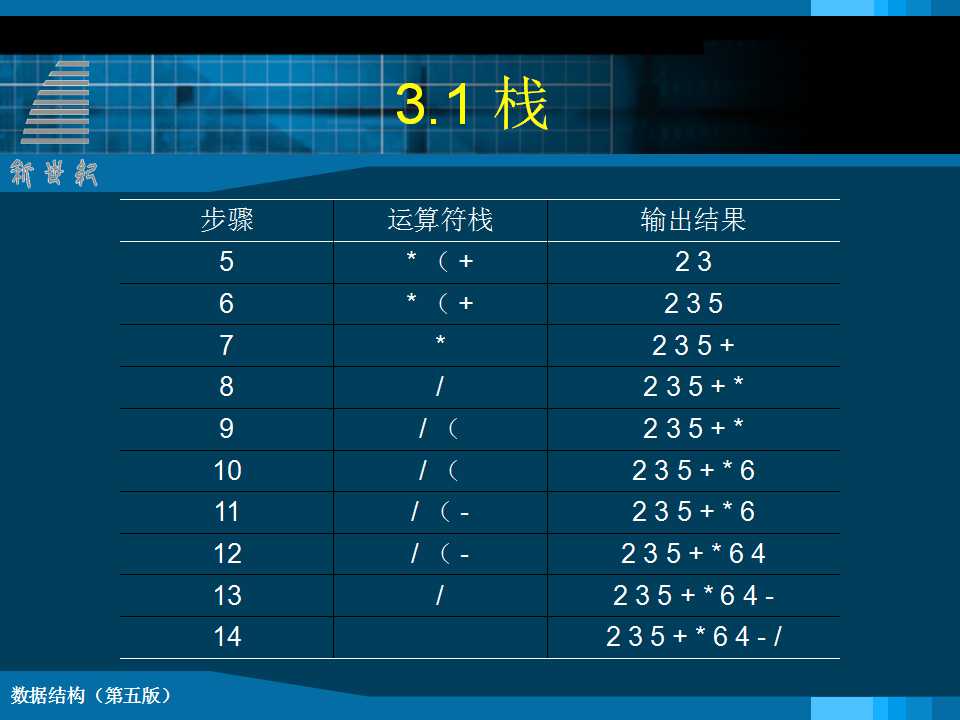
例一、 数制转换

void conversion () {

    InitStack(S);

    scanf ("%d",N);

    while (N) {

      Push(S, N % 8);

      N = N/8;

    }

    while (!StackEmpty(S)) {

      Pop(S,e);

      printf ( "%d", e );

    }

} // conversion

例二、 括号匹配的检验

Status matching(string& exp) {

  int state = 1;

  while (i<=Length(exp) && state) {

     switch of exp[i] {

       case 左括弧:{Push(S,exp[i]); i++; break;}

       case”)”: {

          if(NOT StackEmpty(S)&&GetTop(S)=“(“

            {Pop(S,e);  ii++;}

          else {state = 0;}

          break;  }   … …

  }

例三、行编辑程序问题

while (ch != EOF) { //EOF为全文结束符

while (ch != EOF && ch != '\n') {

      switch (ch) {

       case '#' : Pop(S, c); break;

       case '@': ClearStack(S); break;// 重置S为空栈

       default : Push(S, ch);  break;  

      }

      ch = getchar();  // 从终端接收下一个字符

    }

将从栈底到栈顶的字符传送至调用过程的

数据区；

ClearStack(S);      // 重置S为空栈

if (ch != EOF)  ch = getchar();

例四 表达式求值

void transform(char suffix[ ], char exp[ ] ) {

  InitStack(S);  Push(S, ¢#¢);

  p = exp;  ch = *p;

  while (!StackEmpty(S)) {

      if (!IN(ch, OP)) Pass( Suffix, ch);

      else {            }

      if ( ch!= ¢#¢ ) { p++;  ch = *p; }

      else { Pop(S, ch);  Pass(Suffix, ch); }

  } // while

} // CrtExptree

switch (ch) {

   case ¢(¢ :  Push(S, ch); break;

   case ¢)¢ :  Pop(S, c);

                    while (c!= ¢(¢ )

                       { Pass( Suffix, c);  Pop(S, c) }

                    break;

    defult  :

       while(Gettop(S, c) && ( precede(c,ch)))

          { Pass( Suffix, c);  Pop(S, c); }

       if ( ch!= ¢#¢ )  Push( S, ch);

       break;  

} // switch