压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
介电性质（三）



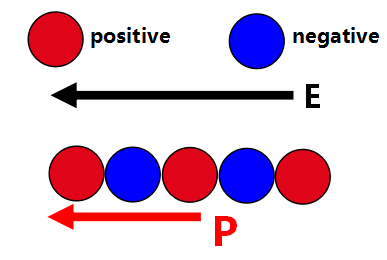
      ◎ 对于离子组成的分子，在电场作用下，正负离子都要产生有限范围的位移，因而使介质产生感应偶极矩。这种感应偶极矩是正负离子之间出现相对位移的结果。

在电场E的作用下，正负离子产生相对位移示意图



      ◎ 如果用ai代表离子位移极化率；Pi代表离子位移的感应偶极矩；E代表电场强度。它们之间的关系为：

      ◎ 为了估计一下离子位移极化率αi的大小，今以二个异性离子组成的分子（如NaCl）为例说明如下：假设电场E的方向与该分子的轴线平行。如图2-3所示，E=0时，二个异性离子之间的距离为a；E≠0时，二个异性离子之间的距离为r=a+△r，其中△r为正负离子在电场作用下的相对位移。

      ◎ 因离子位移而产生的感应偶极矩为：

 

由上两式可得：

 


 ◎ 为了估计一下离子位移极化率αi的大小，今以二个异性离子组成的分子（如NaCl）为例说明如下：假设电场E的方向与该分子的轴线平行。如图2-3所示，E=0时，二个异性离子之间的距离为a；E≠0时，二个异性离子之间的距离为r=a+△r，其中△r为正负离子在电场作用下的相对位移。

      ◎ 因离子位移而产生的感应偶极矩为：

                                                         

由上两式可得：

           

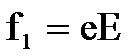
◎ 作用在正负离子的电场力为：

 

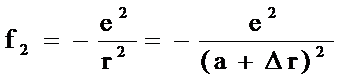
◎ 负离子对正离子的作用力有二个。其一为离子间的吸引力，

  ◎ 另一是离子间壳层电子的排斥力（即电子云之间的排斥力）

 

 

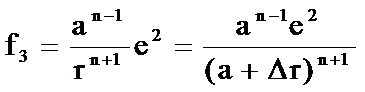
◎ 式中n随离子的电子数增加而增大，一般在6至11之间，可在物理手册中查到。

◎ 根据力的平衡条件有：

  即： 



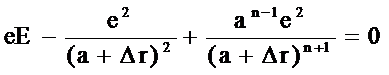
◎ 当电场不是很大时，正负离子间的相对位移Dr很小，即Dr <<a。利用这个条件，可使上式简化。因为：



 ◎ 由这些结果可得


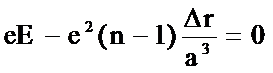
 ◎ 故有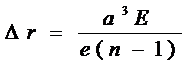

◎ 即得离子位移极化率为：

     

◎ 可见离子位移极化率αi与正负离子半径之和a的立方成正比。

◎ 若将离子间的距离看成离子半径之和，并用r+、r-代表正负离子的半径，上式可写成


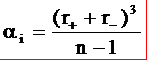
 ◎ 因为离子半径的数量级为10-18厘米，n的数量级在6-11之间，所以离子位移极化率与电子位移极化率同一数量级;或者说，离子位移对极化的贡献与电子位移对极化的贡献同一数量级。









◎ 最后应该指出，在上述氢原子的举例中，当电场不是很大时，正负电荷中心的偏离x很小，利用 x<<a （原子半径）的条件，将氢原子核对壳层电子的作用力简化为

 


◎ 同样，在上述异性离子的举例中，也曾利用 Dr <<(r++r-)条件，将正负离子间的相互作用简化为：

                                             

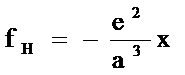
  ◎ 另一方面，我们知道弹性力的特点是：弹性力felas的大小与位移x成正比，方向与位移的方向相反，即：

 

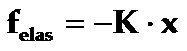
     ◎ 式中比例系数K为弹性系数。

    ◎ 与电子位移极化、离子位移极化中力的表达式相比较，容易看出它们之间完全相似,故称准弹性力。这样一来，在氢原子的例子中可以认为壳层电子是在电场力和准弹性力的共同作用下，达到新的平衡态的；在二个异性离子组成的分子的例子中，正负离子也是在电场力和准弹性力的共同作用下，达到新的平衡态的。