◎ 当电场为零时，组成介质的原子（或离子）其壳层电子的负电中心与原子核（正电中心）重合，不存在偶极矩。当电场不为零时，壳层电子沿电场相反方向移动，原子核则沿电场方向移动（或者说电子云发生畸变）。可见电场的作用是使正负电中心分离。

      ◎ 另一方面，壳层电子与原子核之间的相互吸引力的作用是使正负电中心重合。就是在这二各力的作用下原子处于一种新的平衡状态。在这个新平衡状态中该原子具有一个有限大小的感应偶极矩，用P_e表示感应偶极矩的大小，P_e与电场之间的关系为：

                                      

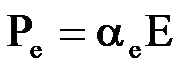
      ◎ 其中α_e称为电子位移极化率。为了估计一下电子位移极化率的大小，我们以氢原子为例说明如下。

      ◎ 设电场E的方向与氢原子轨道平面垂直，电子轨道半径为a，如图2-2。若电子轨道平面偏离原子核的距离为x，则感应偶极矩为：

  

                     

 

 

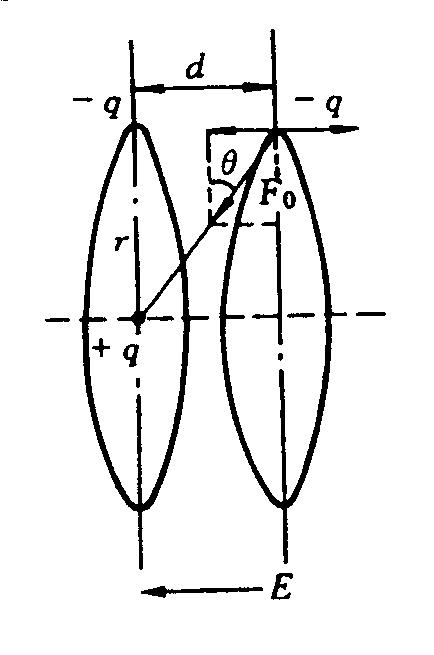
      ◎ 因为壳层电子-e是在电场力f1=-eE和原子核的吸引力 f2=-e2/(a2+x2)共同作用下达到新的力学平衡状态的。 f2在f1方向上的分量为：

      ◎ 当电场不是很大时，正负电荷中心的偏离x很小，即有x<<a，于是上式可简化为：

     

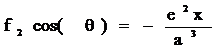
 ◎ 根据力学平衡条件，并考虑到f1与f2cos(q)方向相反，故有：

                即：

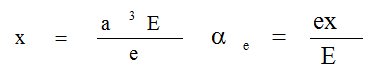故得：所以：

用量子力学计算可得：

      ◎ 可见，氢原子的电子位移极化率α_e与其轨道半径的立方成正比，已知氢原子的轨道半径a=0.5×10^-8厘米，代入到上式即得氢原子的电子位移极化率为α_e=0.56×10^-24 （厘米）³。

      ◎ 此结果与实验相比较，两者数量级相同。应该指出，上式是从最简单的氢原子得到的，对于较复杂的原子，电子位移极化率与轨道半径的立方成正比的关系仍然成立。

      ◎ 从这个关系还可以看出以下几点：

      ◎ 因为原子内层电子受到原子核束缚较大，所以内层电子在外电场作用下产生的位移较小，因而对电子位移极化率的贡献也较小；原子的外层电子，特别是价电子，受到原子核束缚较小，在外电场作用下，这些电子产生的位移最大，因而对电子位移极化率的贡献也最大。可以认为原子中价电子对电子位移极化率的贡献最大。

      ◎ 离子的电子位移极化率的性质与原子的电子位移极化率的性质大致相同。因为原子得到了电子就成为了负离子，原子失去了电子就成为正离子，所以一般负离子的电子位移极化率大于正离子的电子位移极化率。

      ◎ 因为介质的极化强度等于其单位体积中的偶极矩之和。可见极化强度的大小，不仅与偶极矩有关，而且也于单位体积中的偶极矩数目有关（或者说与单位体积内的粒子数有关）。因此，常用α_e /a3来衡量此离子的电子位移对介质极化率（或介电常数）的贡献的大小。如果希望得到介电常数大的材料，就应在该材料中设法加入α_e /a³大于1的离子，例如O^2-、Pb²⁺、Ti⁴⁺、Zr⁴⁺、Ce⁴⁺等离子。