压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
压电振子的振动模式（十六）





薄圆片压电振子的径向伸缩振动:

介电常数

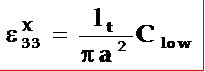
半径a；厚度lt；低频电容Clow

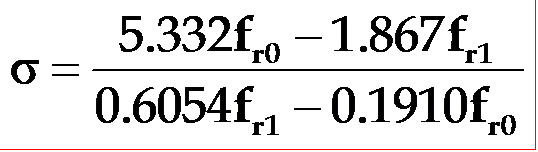
fr0:薄圆片压电振子的基频，fr1:薄圆片压电振子的一次谐波频率。

杨氏模量的确定:



◎薄圆环压电振子的径向振动

◎薄球壳的球径向振动

◎薄片的厚度伸缩振动 



       如图5-9所示，薄圆环的极化方向与z轴平行（即轴向极化），平均半径为r ，厚度为lt，宽度为lw，并有r>>lt以及r>>lw.设圆环的方向为2方向，极化方向为3方向，q增加的方向为1方向。因为圆环的半径远大于圆环的宽度和厚度,所以圆环在外加电场的作用下，可以认为只产生轴对称的径向振动。除了沿圆周（即切向）的应力X1（即Xθ）外，其余的应力、切应力皆等于零。

图 5-9 薄圆环的径向振动




   薄球壳的极化方向与径向平行，球壳内外表面为电极面，球壳厚度为lt，平均半径为r，并有r>> lt，选球的径向为3方向，θ、j的增加方向为1、2方向，其边界条件为:

E1=E2=0,E3¹0；

X3= X4= X5= X6=0，X1≠0, X2≠0。

                      

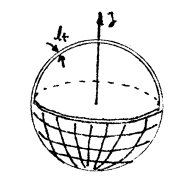
                                     图 5-10 薄球壳的径向振动

 

选应力和电场（X、E）为独立变量，即得薄球壳的径向振动的压电方程组为:

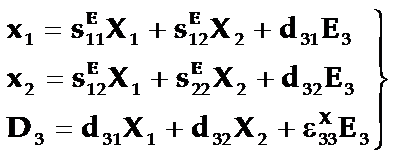（5-71）


对于压电陶瓷的弹性性质和压电性质在与极化垂直的面上是各向异性的，故有X1=X2、sE11=sE22、d31=d32。令:



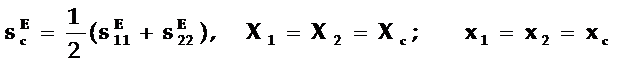
薄片的极化方向与厚度方向平行，片面为电极面，片的长度为l、宽度为lw、厚度为lt，并有l>>lt，lw>>lt。因为只考虑沿厚度方向传播的平面波，频率很高，故可以认为片的侧面被刚性夹住，即可认为:

x1=x2=x4=x5=x6=0，x3≠0

                                   

 设片的绝缘性能良好，没有漏电电流，故可认为D1=D2=0，¶D3/¶z=0，选应变和电位移x、D为独立常数，可选用第四类压电方程组为：

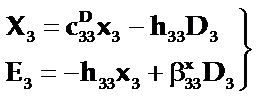              （5-78）

 

波动方程为: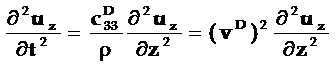  （5-79）

其中uz为沿z方向的位移。

薄片的导纳为: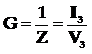

 

 

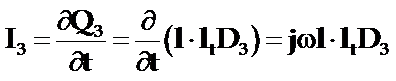
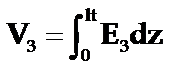
厚度伸缩振动机电耦合系数的定义为:  

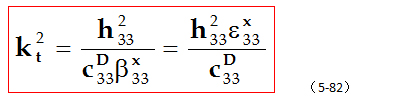
由（5-81）式可得反谐振频率和谐振频率为:







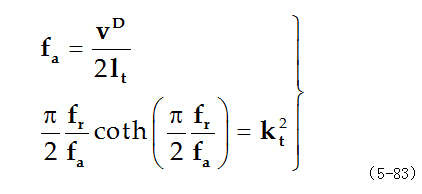
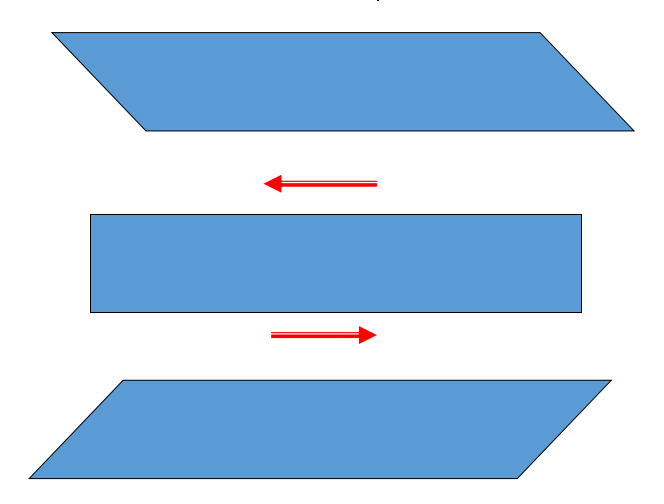
◎宽度弯曲振动模式

◎厚度弯曲振动模式





点振子振动和点电极振子振动：

由于电极质量的负载效应和压电效应的反作用，使压电片的电极区、非电极区的密度以及弹性常数均又微小差别，导致电极区基频f0降到f0’以下。



◎较为详细地求解了薄圆片压电振子的径向伸缩振动;得到机电耦合系数与谐振和反谐振频率之间的关系;

◎简单地介绍了几种其它压电振子的振动模式:薄圆环的径向振动,薄球壳的径向振动,薄片的厚度伸缩振动。

◎切变振动，弯曲振动，能陷振动模。

 

舰船上的声纳：




法国胜利级濒海潜艇（LCS）                          圆柱形声纳阵列

长48.8米，鱼雷舱 长2.5米


英国第4代（Class Astute）攻击型核潜艇;

机敏号（Class Astute） 2008年6月下水；伏击号（Ambush）2010年12月下水；安装二0七六声纳阵列




核潜艇深海相撞


      在2009年2月3日深夜，法国“凯旋”号潜艇与英国皇家海军 的“前卫”号潜艇在大西洋深海发生的相撞事件 。两艘潜艇在同一水域相撞的可能性只有百万分之一。 


                 英国“前卫”号潜艇                     法国“凯旋”号潜艇

◎振动模式的分析对于设计器件非常重要

◎这里只仅对一些简单模式介绍基本原理

◎实际器件的振动模式分析是比较复杂的

◎已经有了成熟的分析软件进行数值分析