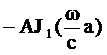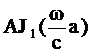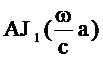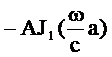波动方程式的解
薄圆片压电振子的波动方程式的通解为：
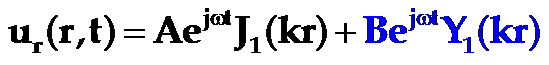
其中:k=
/c；J1(kr)为一阶一类贝塞尔函数； Y1(kr)为一阶二类贝塞尔函数。
J1(kr) First order Bessel function of the first kind。
Y1(kr) First order Bessel function of the second kind。
由于圆片中心为节点，Y1在r=0点发散，所以B=0。
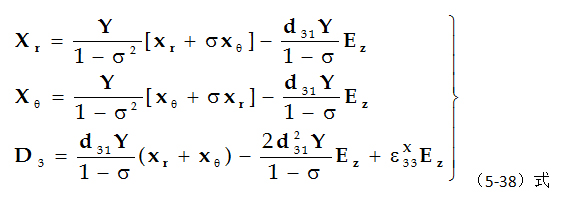
现在来求满足边界条件的解。若薄圆片的边界为机械自由，则在边界上的应力Xr等于零。即:
Xr|a=0
由（5-38）式的第一式：
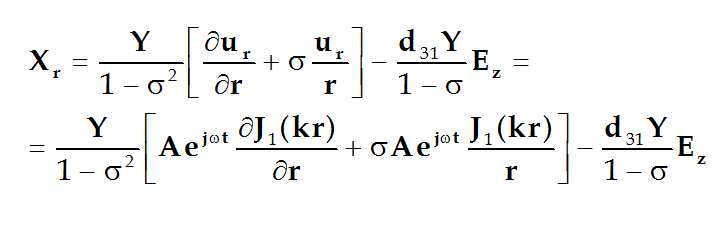
若电场强度分量为: 
并注意到：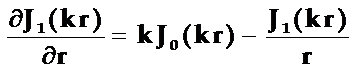 
代入到上式得薄圆片径向伸缩振动的解：
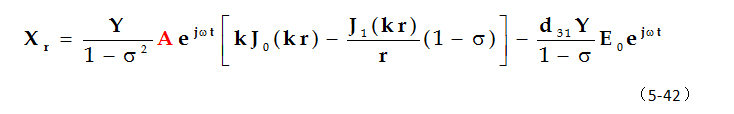
利用边界条件r=a时，Xr|a=0，即可确定任意常数A，由
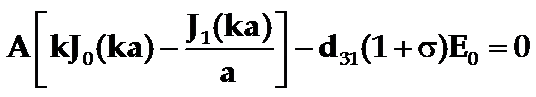
即得：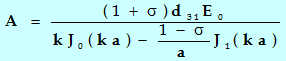 
（5-43）
将（5-43）式代入到（5-41）式即得满足自由边界条件的解为：
(5-44)
由（5-44）式代表的波形，如图5-8所示。
图 5-8 自由圆片的径向伸缩振动（a）自由圆片中的波形（b）自由圆片的伸缩情况
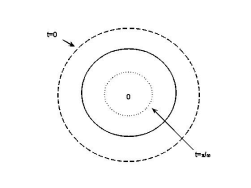
(a) (b)
r | -a
| 0 | a | |
t=0 |
ur(r,0) |
|
0 |
|
t=π/
|
ur(r,π/
|
|
0 |
|
将（5-43）式代入到（5-42）式即得沿r方向的伸缩应力为：
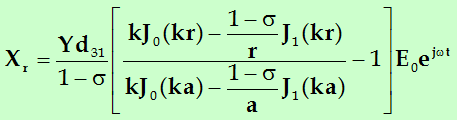（5-45）
沿θ方向的伸缩应力为:
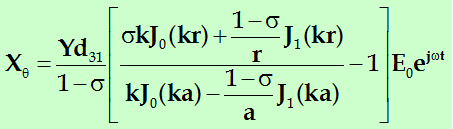（5-46）
沿r方向和θ方向的伸缩应变为:
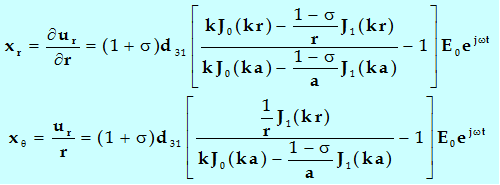（5-47）
电位移为:
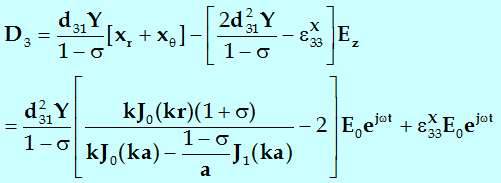
过压电振子电极面的电流I为：
而电极面上的电荷Q为：
积分时注意到：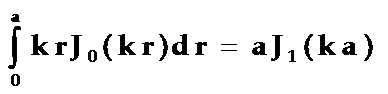
即得：
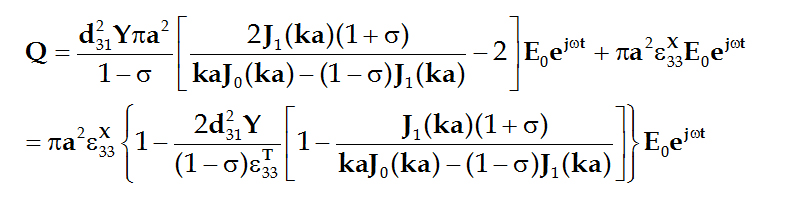
于是得到电流为：
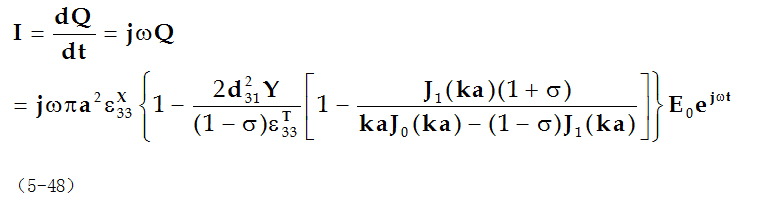
压电振子的等效阻抗Z为：
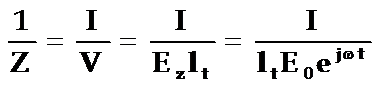
将（5-48）式代入上式得：
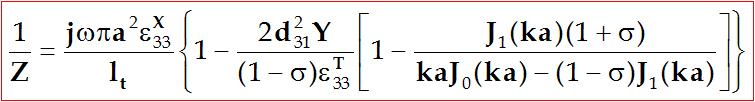
薄圆片压电振子的等效阻抗
(5-49)
k=/c
谐振时压电振子的等效阻抗Z=0，即: G=1/Z=
，这就要求：
即：
或：
（5-50）
其中：r=2πfr，fr=谐振频率。
钛酸钡的泊松比约为
=0.30，代入上式：
查贝塞尔函数的数值表，可得上式最小的根为:
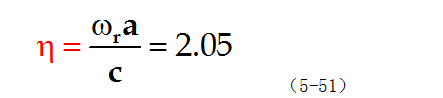
由此得到薄圆片压电振子的谐振频率为：
