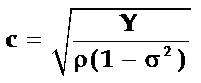压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
压电振子的振动模式（十四）





 (纵向伸缩振动 )

一、压电方程组 + 牛顿第二定律

二、波动微分方程式

三、满足自由边界条件波动微分方程式的解

四、应力、应变、电位移与(x，t)的关系

五、通过振子电极面的电流

六、振子的等效导纳G或等效电阻Z为

七、几种频率及其关系:谐振频率,反谐振频率;串联谐振频率,并联谐振频率;最    大导纳频率,最小导纳频率

八、压电振子有关的常数与谐振频率及反谐振频率的关系

九、压电振子的等效电容、等效电感和等效电阻与材料参数的关系



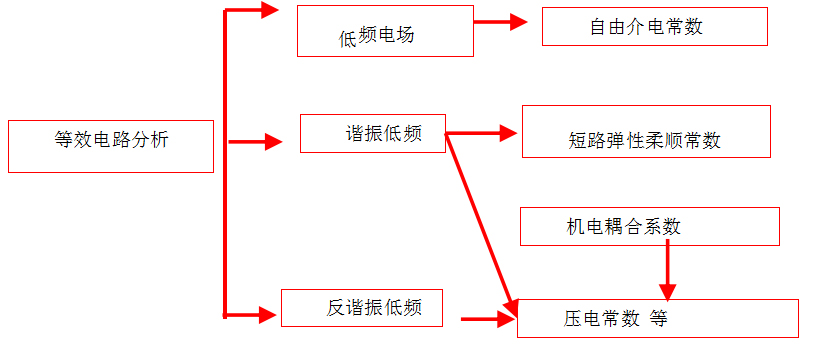
                           α石英（点群为32）的压电常数矩阵



x切α-石英晶片可能的振动模式。x面为电极面。

x方向的纵向（厚度）伸缩振动；

y方向的横向伸缩振动

yz面切变振动。


           


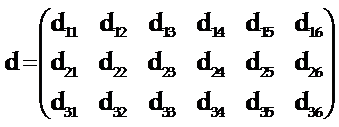
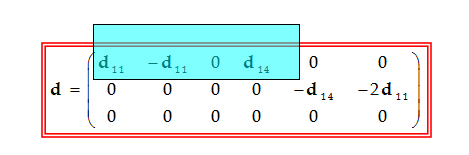
压电陶瓷的压电常数矩阵


压电陶瓷圆片可能的振动模式。z面为电极面。

x、y方向的纵向伸缩振动；

z方向的厚度伸缩振动。





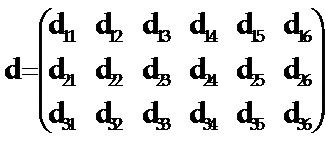
◎根据工作频率（谐振频率）设计的压电晶片的几何尺寸。

◎由于在不同方向上的压电常数不为零（存在压电性），同一激励电场在同一压电晶片会产生多个振动模式。

◎这样在工作频率附近所产生的振动模式就是寄生振动。




◎通过晶片的几何尺寸设计，可以有效地降低寄生振动的产生。

◎另外的方法是开槽技术。

◎不同的振动模式所对应的边界条件不相同。

◎通过在晶片边缘开槽，可以有效地抑制寄生振动。


薄长片压电振子的谐振频率fr为：



                      




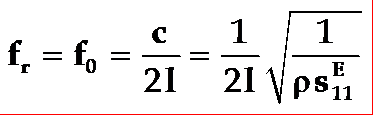
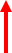
◎薄圆片压电振子的径向伸缩振动

◎其它压电振子: 薄圆环的径向振动,薄球壳的径向振动,薄片的厚度伸缩振动

◎能陷振动模



     对于压电常数d31=d32和弹性柔顺常数s11=s22的压电晶体，例如钛酸钡、铌酸锂等晶体，可用它的z切割薄圆片的径向振动。

用柱坐标（O-rθz），圆片面与z轴垂直。因为是薄圆片，所以可以近似认为垂直于圆片面方向的应力Xz=0。

因为薄圆片只有径向伸缩形变，所以沿r方向和方向的Xr≠0，X≠0，而切应Xrθ=Xrz=Xθz=0。因为电极面就在圆片面上，所以只有沿z方向的电场强度分量Ez≠0，而沿r和q方向的电场强度分量Er=Eθ=0。




  因电极面是等位面，故有（Ez/r）=0。选X、E为自变量，并注意到弹性柔顺常数s11=s22以及压电常数d31=d32，于是薄圆片压电振子的压电方程组为：



             

                                         （5-37）



第二类压电方程组

若以（x、E）为自变量，有（5-37）式可得:


实验上常用杨氏模量Y和泊松比代替弹性柔顺常数sE11、sE12，将Y=1/sE11，=-sE12/sE11关系代入上式得：


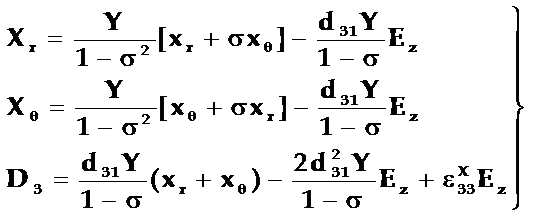
5-38）式就是以应变和电场（x、E）为自变量，用柱坐标表示的薄圆片压电方程组。其中沿r方向的伸缩应变xr=（ur/r），沿θ方向的伸缩应变xθ=ur/r+(uθ/θ)/r。因为薄圆片的径向伸缩振动具有圆对称性，所以((uθ/θ)=0。在此情况下，沿θ方向的伸缩应变简化为xθ=ur/r。




  若圆片密度为ρ，则小的质量为（见图5-7）；若为小块bcde沿径向的位移ρrdθdr，则小块沿径向加速度为2ur/t2。小块的运动方程为：



由于dr和dθ都很小，故有：


 图5-7




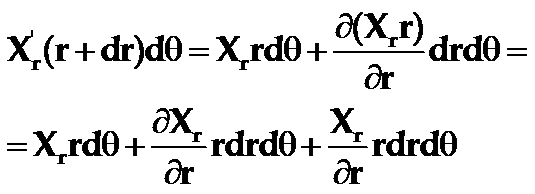
忽略Xθ与Xθ’的差别（即认为Xθ=Xθ’）。将这些结果代入到上式后，即得小块的运动微分方程式为：



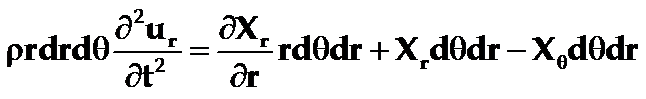
即：


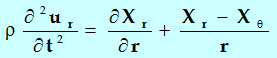
                   （5-39）



      将压电方程组（5-38）式代入上式，并注意到（Ez/r）=0，即得：


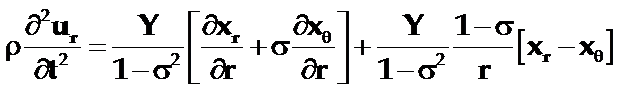
       得到薄圆片压电振子的波动方程为：

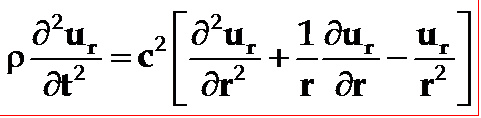
                      （5-40）

其中波速：