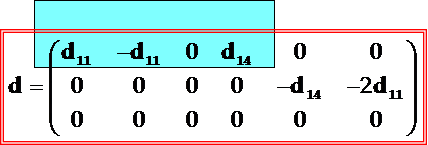
图5-3

当外加电场的频率等于压电振子的谐振频率fr时，压电振子的等效导纳为：

                           

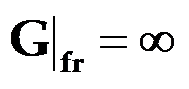
等效阻抗Z|fr=0，电流I3=（实际上I3=极大值）。这种谐振现象与无线电中的LC 串联谐振现象相同。因为LC 串联谐振时，电路中的阻抗=0，电流=。

  所以可以认为谐振时，压电振子在电路中起着一个串联的电容C1和电感L1的作用。在此情况下，压电振子的等效电路如图5-4所示的串联电路。压电振子的谐振频率fr就等于LC串联电路中的谐振频率fs。

谐振时压电振子的等效电路：

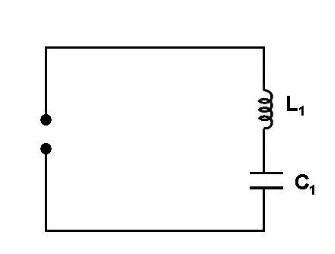
                 图 5-4

当外加电场的频率等于压电振子的反谐振频率fa时，压电振子的等效导纳为：

                      

等效阻抗Z|fa=，电流I3=0（实际上为电流极小）。这种谐振现象与无线电中的LC 并联谐振现象相同。因为LC 并联谐振时，电路中的阻抗无限大，电流为零。

所以可以认为反谐振时，压电振子在电路中起着一个由电容C0和电感L1以及电容C1相并联的作用。在此情况下，压电振子的等效电路如图5-5所示的LC并联电路。压电振子的反谐振频率fa就等于LC并联电路中的谐振频率fp。

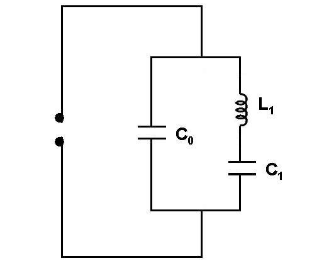     图 5-5

电振子等效电路中的C0、L1和C1与压电常数、介电常数和弹性常数之间的关系：

一方面，压电振子的振动特性是由压电振子的内部矛盾来解决的，即由压电振子的压电常数、介电常数和弹性常数来决定的。

另一方面，压电振子的振动特性又可用LC 串联电路和LC 并联电路反映出来。因此等效电路中的C0、L1和C1与压电常数、介电常数和弹性常数之间存在一定的关联。 

             

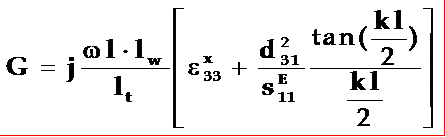
 这个联系可通过压电振子的等效阻抗（或等效导纳）与LC电路中的阻抗加以比较而得到。已知压电振子的等效导纳为：

                                        

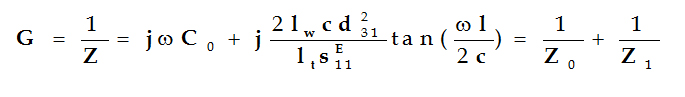
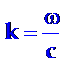
其中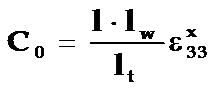：        为分路电容

   为分路阻抗

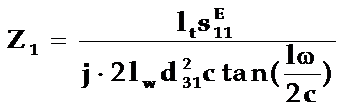        为动态阻抗

使动态阻抗Z1在谐振频率附近展开，因为

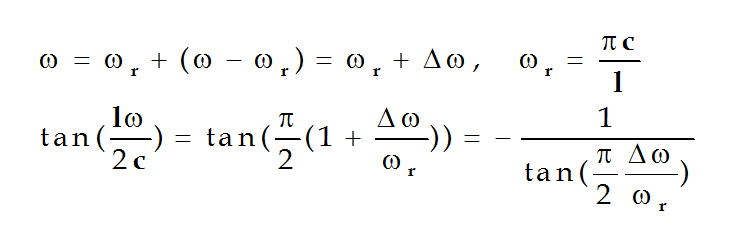
故得：

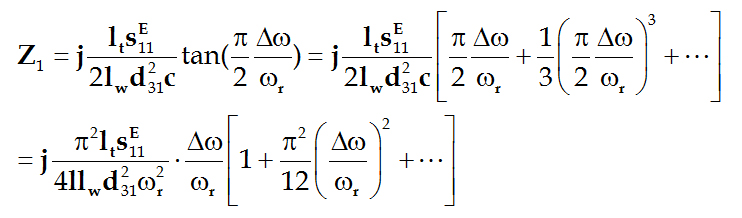
使LC串联阻抗在串联谐振频率：

                                       

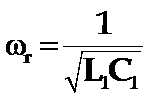
附近展开得：    

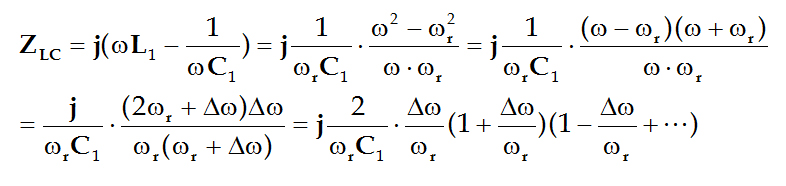
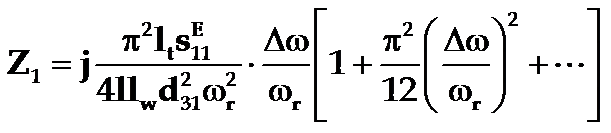
LC串联电路：

比较两式可以看出，在谐振频率附近，取一级近似可得动态阻抗等效于（集总参数）LC串联阻抗，其中联系为： 

  

分别给出了压电振子的等效电感、等效电容和压电常数、弹性常数之间的关系。

注意事项：

通过上述讨论使我们对薄长片压电振子的振动特性、等效电路以及有关的压电常数、弹性常数、介电常数和机电耦合系数的测量有了一个较全面的了解。但是应该注意，上述讨论是在压电振子不存在损耗的条件下进行的。而且是在谐振频率附近的近似条件下得到的。

实际上压电振子总是存在损耗的，只是在损耗很小时，才可能将损耗忽略不计，近似认为是无损耗的压电振子。如果压电振子的损耗不能忽略不计，就需要计入损耗的影响，于是问题就比较复杂了。

这里只提出如下两点注意：

（1）在同样大小的外加交变电场E3=E0cos(wt)作用下，有机械损耗的压电振子的振幅比无损耗的压电振子的振幅小一些，这种损耗在等效电路中的反映就是存在等效电阻R1，如图所示。

            

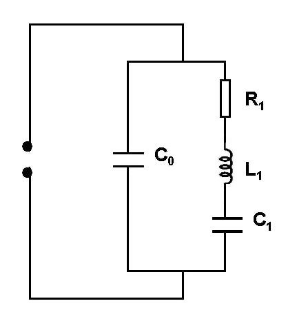
其中等效电路参数为：

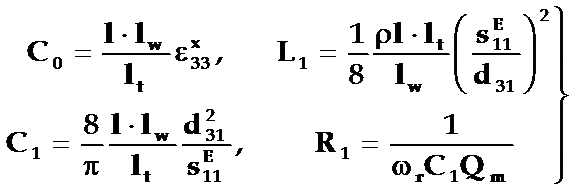
（2）无损耗时，压电振子的谐振频率fr，就等于LC串联电路的谐振频率fs，也等于阻抗最小（电流最大）时的fm。压电振子的反谐振频率fa等于LC并联电路中的谐振频率fp，也等于等效阻抗最大（电流最小）时的测量频率fn，即有：

                     

有损耗时，压电振子的这些频率不再相等，而是：

                   

即有损耗时，实际测量的阻抗最小，电流最大时的频率fm，和阻抗最大，电流最小时的频率fn，既不等于压电振子的谐振频率fr和反谐振频率fa，也不等于LC串联谐振频率fs和LC并联谐振频率fp。

但是当等效电阻R1较小的情况下（即Qm值较高的情况下），fm、fr、fs之间相差较小，fn、fa、fp之间相差也较小。所以实用上常忽略这个差别，近似地认为相等，即：

                 

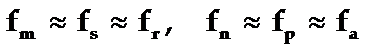
α石英（点群为32）的压电常数矩阵