薄长片压电振子的长度伸缩振动，又称纵向振动，是压电元件中常采用的一种振动方式，也是最简单的振动方式。

    在这一节中除了讨论压电振子的纵向振动特性外，还要讨论压电振子的等效电路以及压电材料的介电常数、弹性常数和压电常数的测量等内容。 

   设d31≠0的压电晶体的zx切割晶片，长度l沿x方向，宽度lw沿y方向，厚度lt沿z方向，并且有l>>lw和lt，电极面与z轴垂直，如图6-3所示。因为l>>lw和lt，长度方向是主要因素，所以只考虑应力分量X1的作用，其它应力分量X2、X3、X4、X5、X6可以忽略不计。 

                

   

 

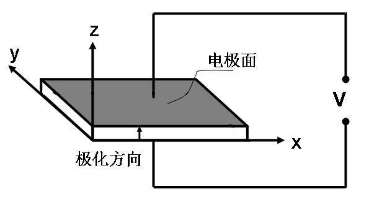
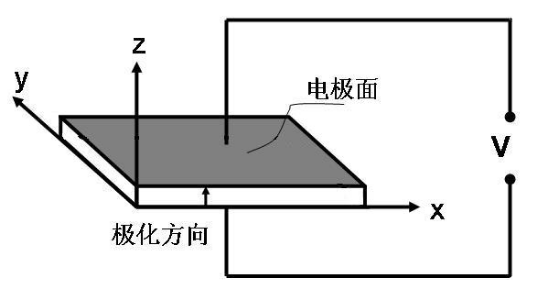
因为电极面垂直于z轴，所以只要考虑电场分量E3的作用，其它电场分量E1、E2可以忽略不计。又因为测量时（或工作时）只是薄片的中心被夹住，片的两端为自由端，即薄片的边界条件为机械自由，在边界上的应力分量X1|边界=0。还有电极面是等位面。

在此情况下，可以选X1、E3为自变量，用第一类压电方程组，即：

                      

 根据牛顿第二运动定律得到薄长片的运动方程为：

                               

             

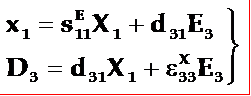
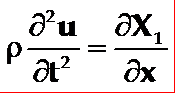
为了得到薄长片压电振子的波动方程，就需要根据压电方程组中应力与应变的关系式：

            

代入波动方程得：

               

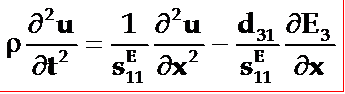
因为压电振子的电极面是等位面，电场分量E3在晶片中是均匀分布的，即有E3/x=0。将这些关系代入上式式即得薄长片压电振子的波动方程为：

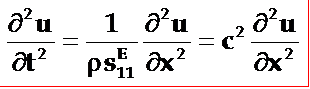 声速：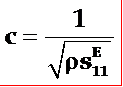

若压电振子是在交变电场 E3=E0ejt，的激发下，通过压电效应产生纵向振动，则上式的通解为：

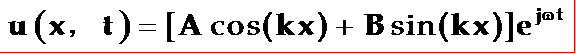
式中：波矢k=/c；A、B为待定系数，由边界条件确定。

   

因为压电振子的两端为自由端，它的机械自由边界条件为:

    x=0时，有X1|x=0=0；  

    x=l时，有X1|x=l=0;

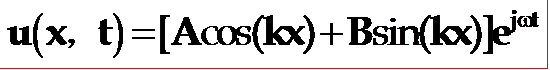
而应力的表达式可以写为：

        

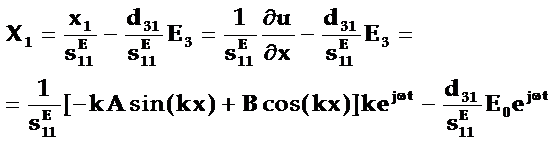
应力表达式包含待定参数A、B

   

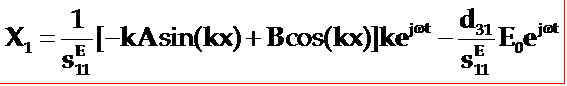
代入边界条件得:

x=0时,X1=0：

                

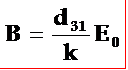
x=l时, X1=0：

       

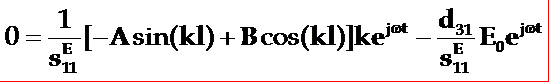
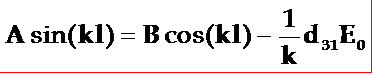
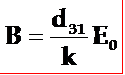
稍加整理即得: 

                 

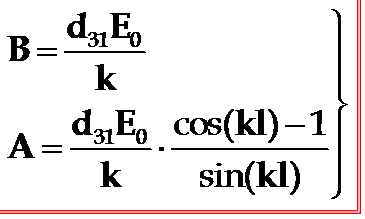
符号有些问题：x表示位置和应变

把A、B代回到波动方程的解中，得到满足边界条件的解为:

位移（形变）是由压电性引起的！

   为了对上式所表示的波形有较具体的了解，在图5-2中，绘出了t=0及t=π/=1/2周期时的波形。从图5-2中可以看出上式代表纵驻波方程式，即在薄长片压电振子中传播的是纵驻波。