压电方程组常数之间的关系
由于边界条件不同,共得到了四类压电方程组,都是晶体的压电性质所遵从的规律,因此它们之间不是互相不相关的,而是存在一定的联系。这个联系一定会在各压电方程组的常数之间反映出来。就是说,各压电方程组的常数之间存在一定的关系。
在四类压电方程组中有:
(1)反映压电晶体弹性性质的常数,如sE11、sD11和cE11、cD11等机械参量;
(2)反映压电晶体介电性质的常数,如x33、X33和x33、X33的等电学参量;
(3)反映压电晶体压电性质的常数,如d31、e31、g31、h31等机电参量。
由第一类压电方程组(4-23)式中的第一式可得:
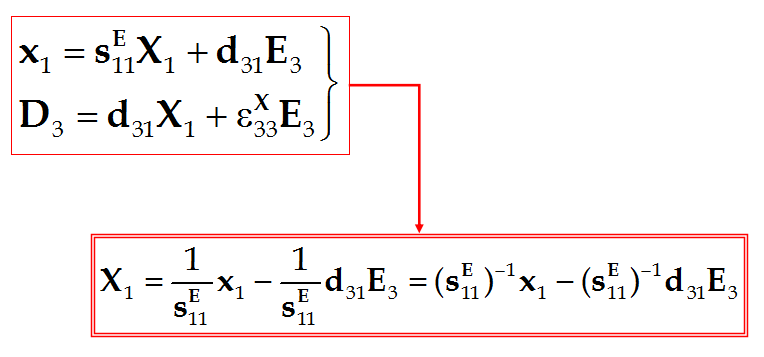
再将此式代入第一类压电方程组(4-23)式中的第二式可得:

整理得:
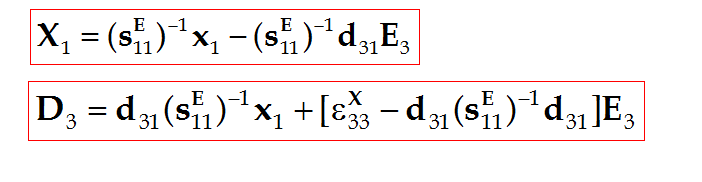
比较第二类压电方程组:

将此两式与第二类压电方程组(4-24)式比较可以得到:
(1)cE11=(sE11)-1这表明z切割的钛酸钡晶片的开路弹性刚度常数cE11为开路弹性柔顺常数sE11的倒数。
(2)e31=d31(sE11)-1= d31cE11这表明z切割的钛酸钡晶片的第二类压电常数e31为第一类压电常数d31与短路弹性刚度常数cE11的乘积,或第一类压电常数d31为第二类压电常数e31与开路弹性柔顺常数sE11的乘积。
(3)x33=X33- d31(sE11)-1d31=X33- e31d31 或X33-x33=e31d31这表明z切割的钛酸钡晶片的自由介电常数X33与夹持介电常数x33之差等于e31与d31只乘积。采用上述类似的方法,可进一步得到诸常数之间的关系如表4-2所示。
钛酸钡z切割晶片各常数之间的关系式
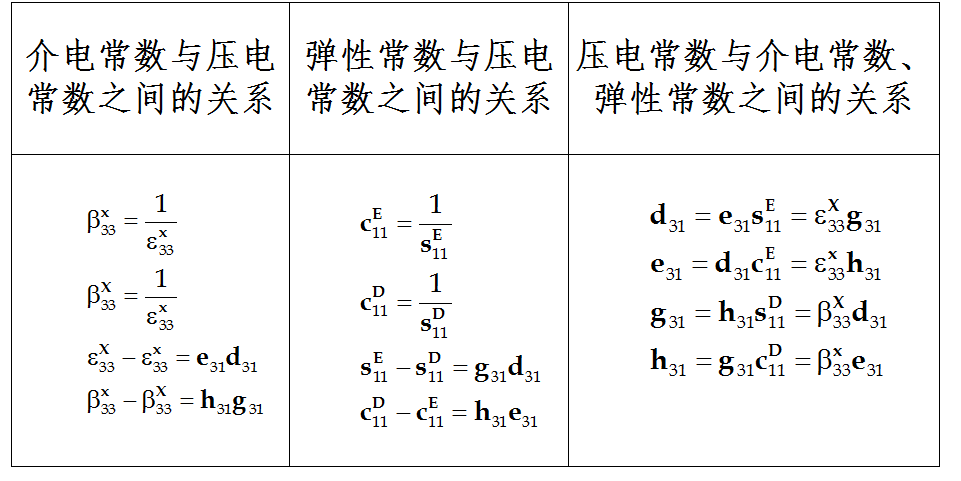
为了进一步说明介电常数X33与x33之间以及弹性常数sE11与sD11之间的差别是什么因素造成的,这里首先要介绍二级压电效应。
二级压电效应又称为次级压电效应。
Secondary piezoelectric effect
当z切割钛酸钡晶片只受到应力X1的作用时,作为弹性介质它将产生弹性应变x1(1),即:
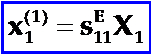
作为压电晶体,X1还将通过正压电效应(即第一次压电效应),产生压电电场E’3,即:

而压电电压将再通过压电效应(即第二次压电效应),使晶片又产生一个附加的压电应变x1(2)
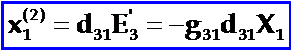
可见附加的压电效应是由于对同一晶片考虑了第二次压电效应的结果,常称为二级压电效应(第一次压电效应称为一级压电效应)。

同样,当晶片只受到电场E3的作用时,作为电介质它将产生极化,相应的电位移D3(1)为:
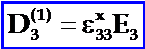
作为压电晶体,E3还将通过逆压电效应(一级压电效应),产生压电应变,x’1即:
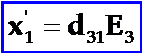
而压电应变将再通过正压电效应(二级压电效应),使晶片又产生一个附加的压电电位移D3(2),
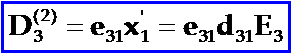
可见附加的压电电位移也是二级压电效应。以上讨论了二级压电效应,要不要再讨论三阶以上的压电效应?
因为二级压电效应比一级压电效应小得多,三级压电效应比二级压电效应小得多,所以一般情况下不再需要考虑三级以上的压电效应。
夹持介电常数与自由介电常数
一般电介质不存在压电效应,因此介电性质与机械性质无关,即有X33=x33=33。
可见对于非压电体,只要用介电常数ij来描写介电性质就够了。但是对于压电体,其介电性质与机械条件有关,所以存在夹持介电常数x33与自由介电常数X33之别。所谓机械“夹持”是晶体被刚性夹具夹住,不论在多大电场作用下,都不能使晶体产生形变。
Clamped (夹持 夹住 夹紧)
这时电场对压电晶体的作用,只能使之产生介电极化,而不能通过二级压电效应产生附加的压电极化。也就是说在机械夹持的条件下,电场在压电体中所引起的作用与它在一般电介质所起的作用相同。机械夹持状态下相应的电位移为:
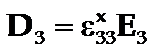
Mechanical free
所谓机械“自由”是压电体处于自由状态。这时压电体在电场的作用下,可以产生自由形变,因此电场在压电晶体中的作用,除了使晶体产生极化外,还能通过二级压电效应使之产生附加的压电极化。也就是说在机械自由的条件下,电场在压电体中所起的作用要大于它在一般非压电体中的作用。
在机械自由条件下,相应的电位移为:
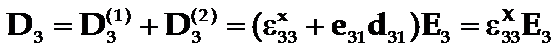
故得:

可见自由介电常数X33与夹持介电常数x33的差别是由于二级压电效应造成的。

一般弹性介质不存在压电效应, 弹性性质与电学边界条件无关,因此即有sE11=sD11=s11。可见对于非压电体只要用弹性柔顺常数sij来描述弹性性质就足够了。但是对压电体,由于存在压电效应,压电体的弹性性质与电学边界条件有关,所以存在短路弹性柔顺常数sE11和开路弹性柔顺常数sD11的差别。
Short circuit
所谓“短路”是测量电路的电阻远小于晶体内电阻,外电路可以认为是短路。在此情况下压电晶体在应力的作用下,通过正压电效应(即一级压电效应)产生的电荷,不可能在电极面上积累,因而不会改变晶体内的电场分布(即E为常数,或E=0)。这时应力对压电晶体的作用,只能使之产生弹性形变,而不能通过二级压电效应产生附加的压电形变。也就是说在短路条件下,应力在压电体中所起的作用与它在一般弹性介质中所起的作用相同,相应的应变是:
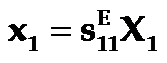
所谓“开路”是测量电路的电阻远大于晶体内电阻,外电路可以认为是开路。在此情况下压电晶体在应力的作用下,通过正压电效应(即一级压电效应)在电极上产生的电荷,不会流走,即晶体的电位移为常数,但晶体内的电场在变。
因此,应力在压电晶体中所起的作用,除了使晶体产生弹性应变x1(1)=sE11X1外,还能通过二级压电效应使晶体产生附加的压电应变S1(2)=-g31d31X1,负号表示压电应变的作用使晶体的形变变小。
这时(开路)总应变为:
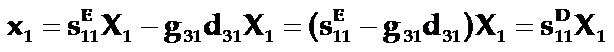
故得:

可见短路弹性柔顺常数sE11和开路弹性柔顺常数sD11的差别,也是由于二级压电效应造成的。
压电增劲效应
其次从sE11 > sD11还可看出:压电效应对晶体弹性的影响是使晶体的弹性顺服常数变小,或者说使弹性劲度常数变大。即:施加同样的外应力,短路的情况下晶体的形变要大于开路的情况下晶体的形变。这一效应又叫做压电增劲效应。
具体材料的弹性常数数值举例如下:

小结:
压电晶体的切割:符号及常见切型
四类边界条件和压电方程组
四类压电方程组常数之间的关系
二级压电效应以及对材料参数的影响


