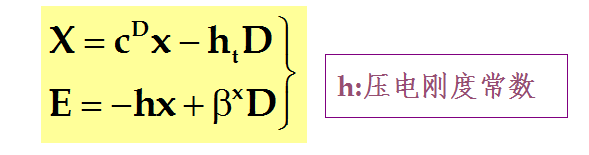对于不同的边界条件，为了运算方便，就必须选择不同的自变量。例如，当边界条件为边界自由条件和短路条件时，以选应力张量X和电场强度E为自变量，应变张量x 和电位移D为因变量较方便，相应的压电方程组就是第一类压电方程组。

与其它各类边界条件相适应的自变量与压电方程组如下。

 

 

如果在测量上述z切割的钛酸钡晶片时，在晶片长度的两端被刚性夹具所夹住，即边界上应变x=0，应力X≠0；而且外电路的电阻远小于晶片内的电阻，在电极面上无电荷积累，即电压保持不变（或E=常数），电位移D¹常数。这时晶片的边界条件为机械夹持和电学短路条件。

在此边界条件下，以选应变张量x和电场强度E为自变量，应力张量X和电位移D为因变量较方便。相应的第二类压电方程组为：

           

式中:cE11=(X1/x1)E称为短路弹性刚度常数，是在外电路为短路的条件下，测得的弹性刚度常数；E33=(D3/E3)x称为机械夹持介电常数，是在机械夹持条件下，测得的介电常数。

一般形式为：

          

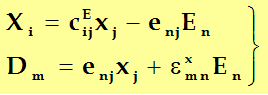
矩阵形式为：

          

 

 

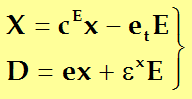
当边界条件为机械自由和电学开路的情况下，以选应力张量X和电位移D为自变量，应变张量x和电场强度E为因变量比较方便，相应的第三类压电方程组为：

              

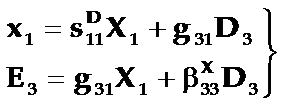
    式中：sD11=(x1/X1)D称为开路弹性顺服常数，是在外电路为开路的条件下，测得的弹性顺服常数；bX33=(E3/D3)X称为自由介电隔离率，它等于自由介电常数X33的倒数，即bX33=1/X33，是在机械自由条件下，测得的介电隔离率，或介电常数的倒数1/X33。

g31称为第三类压电常数，也称压电电压常数。

它的意义为：g31=(x1/D3)X为在机械自由条件下，由于晶片沿z方向电位移D3的变化，引起沿x方向应变x1的变化与D3变化之比。

或者g31=-(E3/X1)D为开路条件下，由于沿x方向应力X1的变化，引起沿z方向电场强度E3的变化与X1变化之比，负号表示应力X1增加时，电场强度E3变小。

一般形式为：

          

矩阵形式为：

 

 

当边界条件为机械夹持和电学开路的情况下，以选应变张量x和电位移D为自变量，应力张量X和电场强度E为因变量比较方便，相应的第四类压电方程组：

 

       

式中：cD11=(X1/x1)D称为开路弹性刚度顺服常数，是在外电路为开路的条件下，测得的弹性劲度常数；x33=(E3/D3)x称为夹持介电隔离率，它等于夹持介电常数x33的倒数，即x33=1/x33，是在机械夹持条件下测得的介电隔离率，或介电常数的倒数1/x33。

h31称为第四类压电常数（也称压电刚度常数）。

它的物理意义为：g31=-(X1/D3)x为在机械夹持条件下，由于沿z方向电位移D3的变化，引起沿x方向应力X1的变化与D3变化之比，负号表示电位移D3增加时，应力X1变小。

或者h31=-(E3/x1)D为电学开路条件下，由于沿x方向应变x1的变化，引起沿z方向电场强度E3的变化与x1变化之比，负号表示应变x1增加时，电场强度E3变小。

一般形式为：

          

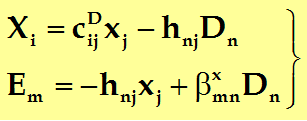
矩阵形式为：