最后得到钛酸钡晶体zx切割晶片的压电方程为（以应力X和电场强度E为自变量）：

       

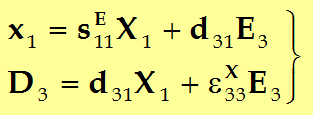
上被称为第一类压电方程组。

注意：电位移只是来自电场的贡献；介电常数也与力学量有关；机电耦合

 

一般形式为：

         

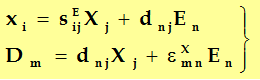
矩阵形式为：

 

这个方程组的特点：在于以应力X、电场强度E为自变量，应变x、电位移D为因变量；即认为应变x、电位移D的变化是由应力X、电场E变化引起的。式中还包括了短路弹性柔顺常数sE11，自由介电常数eX33以及压电常数d31。

 

 

    通常测量样品的频率特性（谐振频率和反谐振频率）时，晶片的中心被夹住，晶片的边界却处于机械自由状态。这时边界上的应力X|边界=0，应变x≠0，这样的边界称为机械自由边界条件，或称边界自由条件。

    但是应该注意：边界自由条件只表示样品在边界上的应力为零，样品内的应力一般情况下并不等于零，只有在低频情况下，样品内的应力才接近于零，所以在边界自由和低频的条件下，测得的介电常数才是（机械）自由介电常数X33。

若测量电路的电阻远大于晶片的内电阻，则可认为外电路处于开路状态，这时电极面上自由电荷保持不变，样品内的电位移D为常数（或D=0）。这样的电学边界条件称为（电学）开路边界条件，简称开路条件。在开路条件下测得的弹性柔顺常数才是开路弹性顺服常数sDij。

BC: boundary conditions

四类边界条件：

机械边界条件有两种，即:

                    边界自由条件， 边界夹持条件；

                Free and Clamped mechanical BC

电学边界条件也有两种，即:

                     短路条件， 开路条件；

                 Short and Open electrical BC

从二种机械边界条件和二种电学边界条件中各选一种，就可组成四类不同的边界条件：

（1）机械自由和电学短路条件；

（2）机械夹持和电学短路条件；

（3）机械自由和电学开路条件；

（4）机械夹持和电学开路条件。