（2）石英晶体的独立压电常数只有d11与d14两个，它们的数值是：
d11=-2.31´10-12库仑/牛顿，
d14= 0.73´10-12库仑/牛顿。
在压电材料中属于比较小的数值。
对于一般的情况，例如属于三斜晶系1（C1）点群的压电晶体是完全各向异性的，独立的压电常数共有18个，用矩阵表示即为：
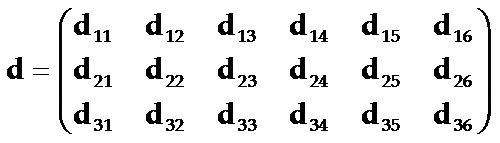
可见压电常数d的矩阵形式是一个三行六列矩阵，即d是一个三级张量。一般情况下正压电效应的表示式为：
或简写为：
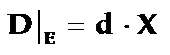
或：
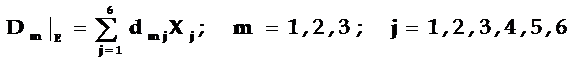
当晶体受到电场E的作用时，晶体产生与电场成线性比例的畸变，这个现象称为逆压电效应。逆压电效应的产生是由于压电晶体受到电场的作用时，在晶体内部产生应力，这个应力常称为压电应力。通过压电应力的作用，产生压电形变。
仍以石英晶体为例说明如下。
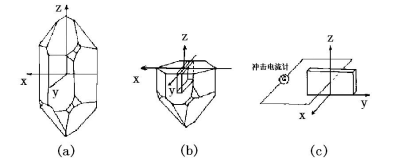
（1）选用石英晶体的x切割晶片，以x面为电极面。当晶片只受到x方向的电场分量E1作用（应力张量X=0）时，分别在x方向和y方向产生应变x1和x2以及切应变x4，这些应变都与E1成正比，即：
其中下标X表示应力张量X=0。
（2）以y面为电极面，当晶片只受到y方向的电场分量E2作用时，分别产生切应变x5和x6，这些应变都与E2正比，即：
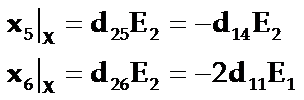
（3）以z面为电极面，当晶片只受到z方向的电场分量E3作用时，晶片不产生任何形变。
综合上述结果，得到石英晶体的逆压电效应表示式，用矩阵表示为：
从上式可以看出：
（1）对于石英晶体不是在任何方向上都存在逆压电效应，只有在某些方向，在某些电场作用下，才能产生逆压电效应。例如，当x方向电场分量E1作用时，可产生压电形变x1和x2以及压电切应变x4。又如当z方向电场分量E3作用时，晶体不会产生任何形变。
（2）逆压电常数与正压电常数相同，并且一一对应。
（3）有正压电效应方向就有相应的逆压电效应。晶体中那个方向上有正压电效应，则此方向上一定存在逆压电效应。
对于一般的情况，例如三斜晶系中的压电晶体，它的逆压电效应用矩阵表示即为：
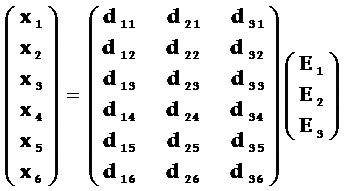
将正压电效应方程式与逆压电效应方程式比较，可见逆压电效应表示式中，压电常数矩阵是正压电常数矩阵d的转置矩阵。常用表示dt。dt是一个六行三列的矩阵，于是逆压电效应方程式可简写为：
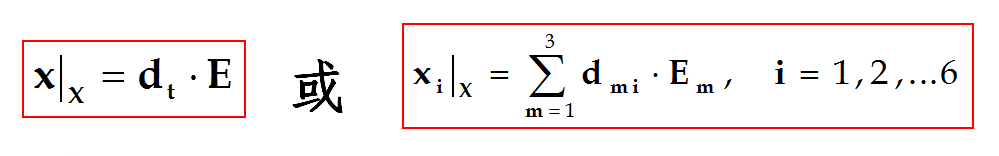
压电晶体与其它晶体的主要区别在于压电晶体的介电性质与弹性性质之间存在线性耦合关系，而压电常数就是反映这种耦合关系的物理量。
由（4-17）式可得，dni=(
xi/En)X，即应力X为零时（或X为常数时），由于电场强度分量En的改变引起应变分量xi的改变与电场强度分量En的改变之比。或者说dni为应力为零时，压电晶体的应变分量xi随电场强度分量En的变化率。
由（4-13）式可得，dmj=(Dm/Xj)E，为电场强度为零时（或E为常数时），由于应力分量Xj的改变引起电位移分量Dm的改变与应力分量Xj的改变之比。或者说dmj为电场强度为零时，压电晶体的电位移分量Dm随应力分量Xj的变化率。
实验上常根据dmj=(Dm/Xj)E来测量压电晶体的压电常数dmj。
