压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
压电效应与压电方程组（二）




  

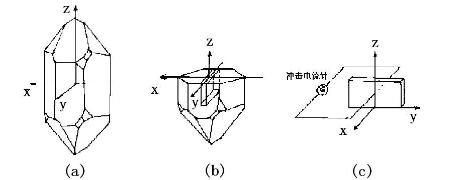
在晶体x轴垂直的方向上，切下一块薄晶片，晶片面与x轴垂直，如图4-1b所示，称为x切割。更详细的说法是：如果晶片的厚度沿x轴方向，长度沿y方向，则称为xy切割。该晶片的长度为l，宽度为lw，厚度为lt，与x轴垂直的二个晶面上涂上电极，并与冲击电流计连接（测量电量用），如图4-1c所示。

 

（1）当晶片受到沿x轴方向的力Fx作用时，通过冲击电流计，可测出在x轴方向电极面上的电荷q(1)1。并发现x轴方向电极面上的电荷密度（q(1)1/llw）的大小与x轴方向单位面积上的力（Fx /llw）成正比，即：

                   

因为（q(1)1/llw）是极化强度分量P(1)1；（Fx/llw）为x方向的应力X1，于是得到

 

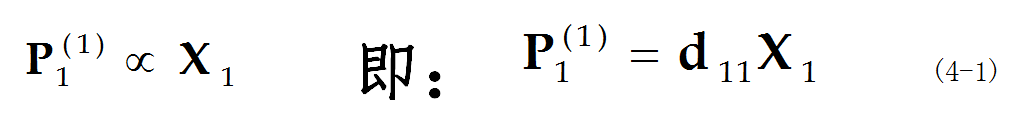
 式中：P(1)1为晶片只受到x方向的应力X1作用时，在x方向产生的极化强度分量，比例系数d11称为压电常数。

          

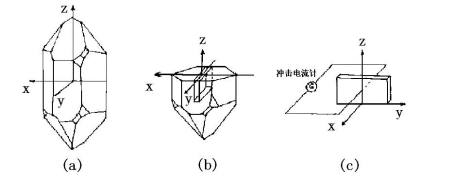
（2）当晶片受到沿y方向的力Fy作用时，通过冲击电流计，可测出在x轴方向电极面上的电荷q(2)1，并发现x方向电极面上的电荷密度（q(2)1/llw）的大小与y方向单位面积上的力（Fy/lwlt）成正比，因为（q(2)1/llw）是极化强度分量P(2)1。

（Fy/lwlt）为y方向的应力X2，于是有

 

 式中，P(2)1为晶片只受到y方向的应力X2作用时，在x方向产生的极化强度分量，比例系数d12也称为压电常数。

实验上还发现当X1=X2时，存在P(2)1= -P(1)1，由此可得d11=-d12，即石英晶体的压电常数d12的大小等于压电常数d11的负值。

 

 

（3）当晶片受到沿z方向的力Fz作用时，通过冲击电流计，并发现x方向电极面上不产生电荷。即有

 

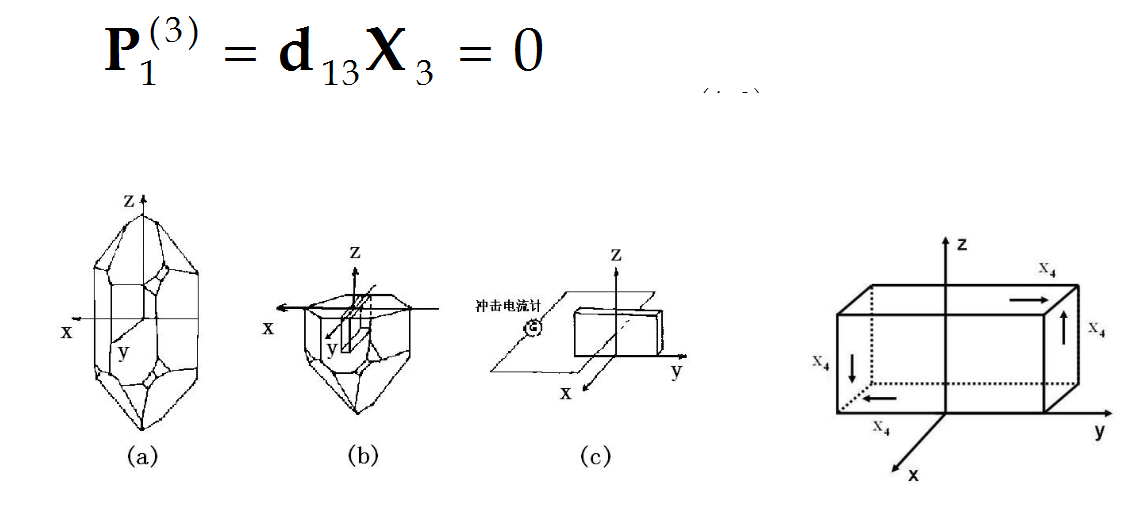
 （4）当晶片受到切应力X4作用时，通过冲击电流计，可测出在x方向电极面上的面电荷密度（q(4)1/llw）= P(4)1，并发现P(4)1与X2成正，于是

              (4-4)

式中： P(4)1为晶片只受切应力X4作用时，在x方向产生的极化强度分量，比例系数d14称为压电常数。

           

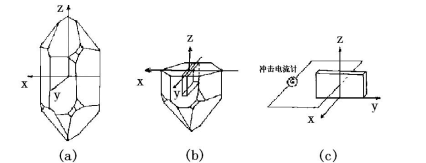
（5）当晶片受到切应力X5或X6作用时，通过冲击电流计，并发现x方向电极面上不产生电荷，于是有

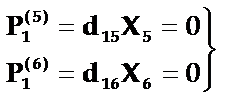                   (4-5)

因为X5¹0，X6¹0，故压电常数d15=0，d16=0，由此可见，对于x切割的石英晶片，当受到切应力X5或X6的作用时，在x方向并不产生压电效应。

综合上述实验结果得到，选x方向为电极面，当电场E=0时，应力张量X对x方向的极化强度分量P1的贡献为：

      

        

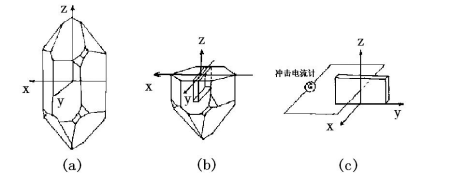
当选y方向为电极面，重复上述实验，当电场E=0时，应力张量X对y方向的极化强度分量P2的贡献为：



即石英晶体的压电常数d25=-d14，d26=-2d11。

        

当选z方向为电极面，重复上述实验，当电场E=0时，应力张量X对z方向的极化强度分量P3的贡献为：

               （4-8）

根据（4-6）、（4-7）以及（4-8）式的结果，可得到石英晶体的正向压电效应表示式用矩阵表示为：

  

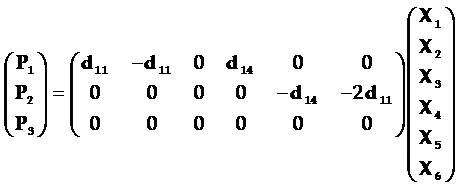
在压电物理中常用电位移D代替极化强度P，当电场E=0时，D=e0E+P=P，电位移的三个分量：D1=P1，D2=P2，D3=P3。将这些关系代入到（4-9）式，即得到用电位移分量与应力分量表示的石英晶体正向压电效应的表示式为：

          

从以上两式式可以看出：

（1）对于石英晶体不是在任何方向上都存在压电效应，只有在某些方向上，在某些力的作用下，产生才能出现正压电效应。例如，在石英晶体x方向，只有X1、X2、X4作用时，才能在x方向压电效应，而X3、X5、X6不能在x方向压电效应。在石英晶体的z方向，不论在什么方向作用多大的力，都不能在z方向压电效应。

（2）石英晶体的独立压电常数只有d11与d14两个，它们的数值是：

d11=-2.31´10-12库仑/牛顿，

d14= 0.73´10-12库仑/牛顿。

在压电材料中属于比较小的数值。