压电器件中有一类重要和应用广泛的领域：声表面波器件（Surface Acoustic Wave Devices, SAWD）, [电®声®电]

对于各向异性的晶体，它的弹性性质由胡克定律来描述。

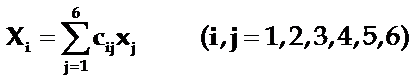
这里c为弹性劲度系数。

而应变张量元为： 

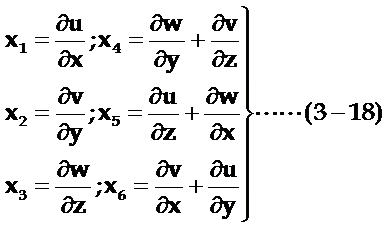
式中u、v、w代表晶体中质点位移沿x、y、z方向的分量。

质点的运动方程可写为

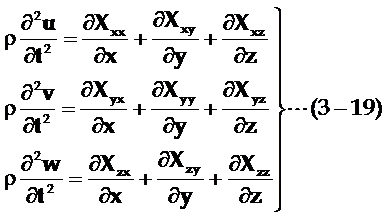
式中r代表晶体密度，按（3-8）对应关系，上式可改写为

把（3-12）、（3-18）代入上式，原则上就得出波的传播方程式，从而解出位移三个分量u、v、w。

显然，这样的运算比较繁杂。下面我们介绍另外的方法求解晶体中所传播的弹性波方程的方法。

由于讨论的是各向异性介质，波在不同方向上的传播情况显然是不同的。例如，各个方向上的有效弹性常数不同，波的传播速度也不同。

下面我们具体来考虑某一方向上的传播情况。设任意传播方向j，它的方向余弦为l、m、n，在这个方向上的某点P(x、y、z)同原点的距离为j ，则

显然，P的位移分量u、v、w依赖于（即质点的位移）波的传播方向l、m、n，所以可以把（3-18）式改写为：

应力和应变之间由胡克定律联系

（3-21）式代入上式得到质点位移（u,v,w）与应力(T₁-T₆)之间的关系

质点运动方程可写为： 

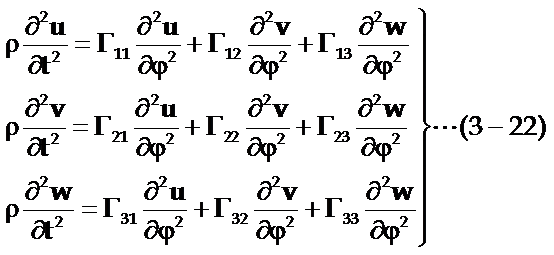
式中G_ij称为克利斯托夫（Christoffel）张量，它共有六个张量元，组成对称二级张量。

克利斯托夫（Christoffel）张量G_ij的表示式：

设x表示沿j传播的波在晶体中所引起的弹性位移矢量，它的分量为u、v、w。位移矢量x的方向余弦为p、q、r，那么，

x为位移矢量x的长度。

把x的表达式代入到质点运动方程（3-22）式中得到： 

这就是j沿方向传播的弹性波方程，式中c_eff代表沿方向晶体的有效弹性常数。

晶体沿方向j的有效弹性常数c_eff须满足下列方程组：

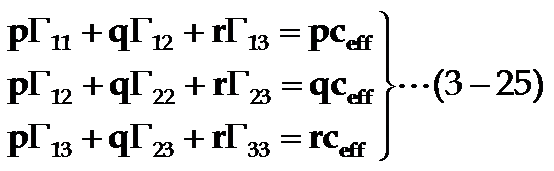
因而得久期方程

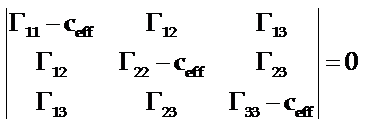(3-26)

由此可知，一般情况下，c_eff有三个解c_eff,i(i=1、2、3)，它们分别对应于三个不同的波，其对应的传播速度为（c_eff，i/r）^1/2。

对于这三个波，质点分别有相应的三个位移，把由久期方程 （3-26）式求得的c_eff,i代入到有效弹性常数（3-25）式，即可解出与c_eff,i对应的位移的方向余弦p_i、q_i、r_i。

下面以立方晶系为例，对上面的讨论加以说明。

立方晶系的弹性劲度常数

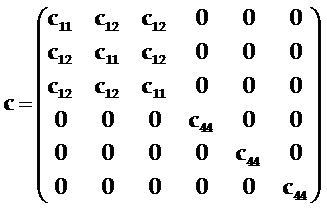
立方晶系只有三个独立的弹性常数c₁₁、c₁₂和c₄₄。

由（3-23）式可得到它的克利斯托夫张量为：

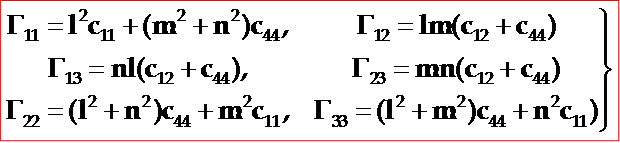
（3-27）

把上式代入到久期方程（3-26）式，得到：

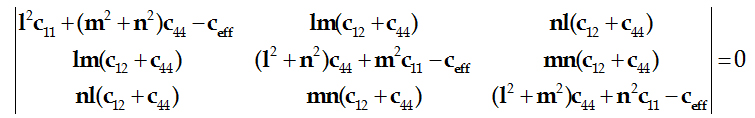
(3-28)

当j沿[100]方向时，l=1、m=0、n=0，这时上式（3-28）变为 

即可解得C_eff,1=C₁₁，C_eff,2=C₄₄，C_eff,3=C₄₄。把这些式子代入到（3-24）式，可得到三个弹性波的波速和对应质点的位移方向。

沿[100]方向三个弹性波的波速和对应质点的位移方向

(1)

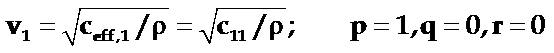
即x沿[100]方向；

(2)

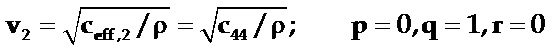
即x沿[010]方向；

(3)

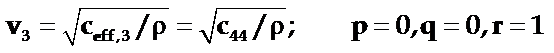
即x沿[001]方向；

当j沿[110]方向时，l=m=1/  、n=0，同理可知也有三个弹性波：

(1) 

即x沿[110]方向；

(2)

即x沿[001]方向；

（3）

即x沿[ ]方向；

当j沿[111]方向时，l=m=n=1/   ，三个弹性波为： 

(1)

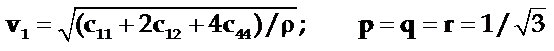
即x沿[111]方向；

（2）和（3）

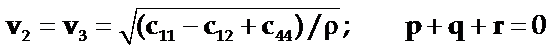
即x沿垂直于[111]方向平面上的任意方向；

从以上讨论可以知道，x弹性波在晶体中传播一般有三个不同速度，其中一个波的位移方向和波矢方向j相同，我们把它称为纵波；而另外两个波的位移方向垂直于波矢方向，则称为横波。

最后还应指出：对于各向异性介质（如单晶）来说，在一般的方向上，虽有三个传播速度，但是对应于某一传播速度，往往质点位移方向既不平行也不垂直于波矢方向，因此纵波和横波不能加以分辨，只能在某些特殊方向上，这种分辨才有可能。

地球包括表层的岩石和地球深部物质，都不是完全的弹性体，但是地震波的传播速度很大，波动给介质带来的应力和应变是瞬时的，能量的消耗很小，此可以近似地把地震波看作弹性波。

从震源发出的波动有两种成分: 振动方向与传播方向一致的纵波振动方向与传播方向垂直的横波。纵波的传播速度较快，在远离震源的地方纵波先到，横波次之。除体波外，还存在表面波，传播速度比体波慢，比体波晚到，但振幅往往很大，振动周期较长。