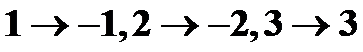压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
晶体的弹性性质（四）






• 属于三斜晶系1点群的压电晶体是完全各向异性的，独立的弹性常数共有21个。

• 属于立方晶系的23点群和3m点群的压电晶体，是对称性最高的晶体，它接近于完全各向同性。独立的弹性常数只有三个。

• 属于四方晶系4mm点群的BaTiO3晶体，独立弹性常数共有六个。

• 属于六角晶系32点群的a-石英晶体和点群的LiNbO3，独立弹性常数都是六个。

• 属于正交晶系mm2点群的铌酸钡钠（Ba2NaNb5O15）晶体和222点群的酒石酸钾钠（NaKC4H4O6×4H2O）晶体，独立弹性常数有9个。

• 根据Neumann原则，晶体的对称性不仅表现在结构上，也表现在它的物理特性上，因此晶体的弹性常数必然和晶体的对称性密切相关。

• 通常是晶体的对称性愈高，其独立的弹性常数分量数目愈少。

• 为了确定晶体具有的独立弹性常数，通常有两种方法：一种是下标代换法；另一种是坐标变换法。由于坐标变换法具有普适性。因此我们首先讨论弹性常数张量的坐标变换。

• 此外对于各向异性晶体，其弹性常数的数值都是对于正常晶体坐标系给出的，而实际使用的晶片往往是旋转切割的，其坐标选取与正常的晶体坐标系不同，为此必须将弹性常数张量从晶体坐标系变换到实际采用的坐标系中下面首先讨论应力和应变张量的坐标变换。

• 应力张量X和应变张量x坐标变换

• 
设新旧坐标系分别为O-x1,x2,x3和O-x’1,x’2,x’3,如右图示。新旧坐标系的坐标轴的方向余弦为：

  


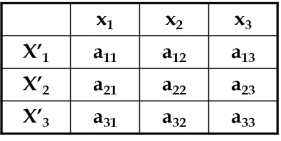
上述新旧坐标系的方向余弦的9个数构成一个正交矩阵



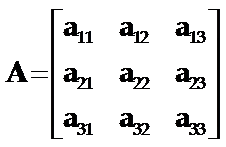
因为应力X和应变x是二阶张量，所以它们的坐标变换遵从二阶张量的变换规则。首先考虑应力张量的坐标变换，设X’和X分别为坐标变换前后的应力张量，则根据二阶张量的变换法则有 X’=A×X×A–1 或 [X’]=[A][X][A-1]

采用爱因斯坦脚标重复自动求和规则，变换前后应力的分量可写成：X’ij=aimajnXmn。

将上式展开，首先考虑到i=j=1时应力分量X’11，有:

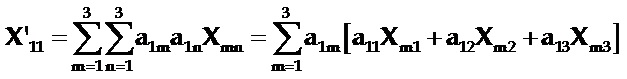
将上式完全展开，得




整理，得:

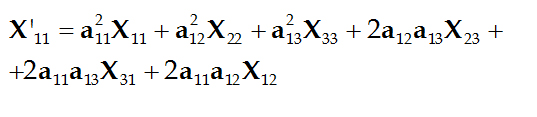
应力矩阵元采用缩写下标，上式可写为:

同理可以得出变换后应力张量的其余五个分量










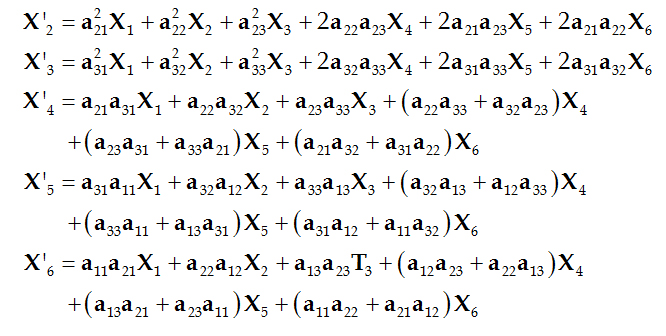
上面六组联立代数方程组的矩阵形式

      注意矩阵M、N的不同！













逆矩阵  

使用完全类似的方法,还可以求出应力张量的逆变换矩阵[M]-1和应变张量的逆变换矩阵[N]-1,即

[X]=[M]-1[X’], [x]=[N]-1[x’]

并得出如下关系式:

[M]-1=[N]t, [N]-1=[M]t

式中, [M]t为[M]转置矩阵,[N]t为[N]的转置矩阵.

弹性常数张量的坐标变换

设胡克定律在原是坐标中表示为：

[x]=[c][X], [X]=[s][x]

在坐标变换后新坐标系中表示为：

[x’]=[c’][X’], [X’]=[s’][x’]    


根据新旧坐标变换关系式有：

[x’]=[M][x], [X]=[N]-1[X’]  

故有：[x’]=[M][c][X]=[M][c][N]-1[X’]

将上式和(1)比较得出弹性刚度常数在新旧坐标系中的变换关系为：

[c’]=[M][c][M]t            (2)

同理,可得到弹性柔顺常数在新旧坐标系中的变换关系：

[s’]=[N][s][N]t       (3)

由式(2)和(3)可知,只要知道了应力和应变张量的坐标变换矩阵[M]和[N],就可以求出弹性常数张量的坐标变换。

为了确定晶体独立弹性常数,必须根据晶体的对称性,并应用Neumann原则来完成,现在以三角系3m点群晶体为例子来进行讨论。

对于三角晶系3m点群的晶系,x=0的面是对称面,z轴为三阶转轴,根据Neumann原则,晶体的弹性常数张量经上述对称性操作,其值不应改变。

对于x1=0的对称面,新旧坐标选取如下图,新旧坐标系之间的方向余弦矩阵为:


 







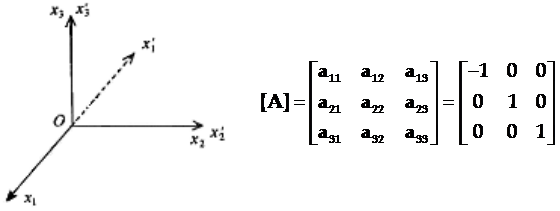
将上式代入应变张量矩阵的坐标变换矩阵[N]为：



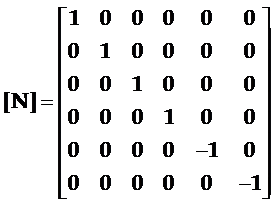
将坐标变换矩阵代入弹性柔顺常数在新旧坐标系中的变换式：[x’]=[N][x][N]t得，

由于x=0面为对称面,新旧坐标系的弹性柔顺常数矩阵应该相等,即sij’=sij,为此只有下式成立时才能满足

s15=s16=s25=s26=s35=s36=s45=s46=0

所以弹性柔顺常数矩阵变成如下:

X=0面是对称面的弹性常数矩阵

由于z(x3)轴为三阶转轴,新旧坐标系选取如图示,对此新旧坐标系的变换矩阵为:











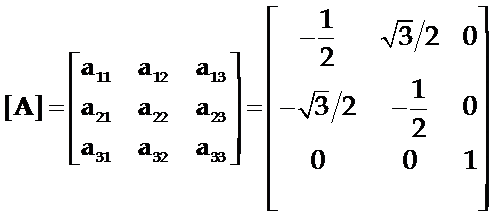
将上式代入坐标变换矩阵



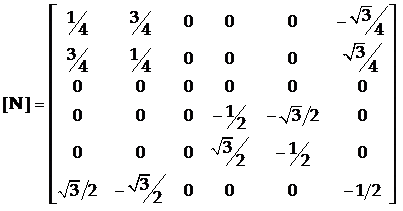
[N]的转置（transpose）矩阵是

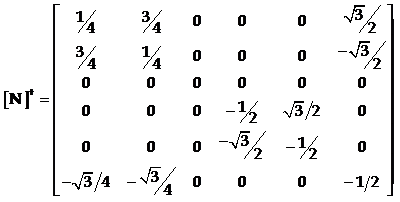
将[N]和[N]t代入[x’’]=[N][x’][N]t,

再令[x’’]=[x’],得到

s11=s22,, s13=s23, s14=-s24,s34=0, s44=s55,s56=2s14, s66=2(s11-s12).

又因为:具有镜面对称的弹性常数矩阵


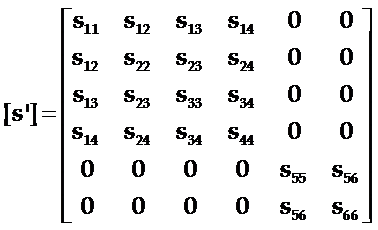
所以：m+3之后

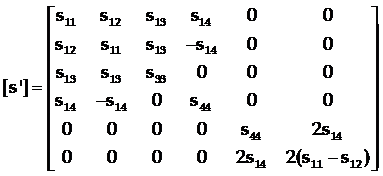
由此可见,独立的弹性顺服常数只有s11, s12, s13, s14, s33, s44共六个

足标代换法

以222点群为例。222点群表示有三个二次旋转轴，分别沿x,y,z方向。先考察沿z轴的二次旋转轴。因为z轴是二阶轴，当晶体绕z轴转180°后，晶体坐标变换为，



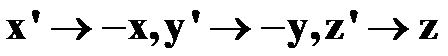
或