还可以采用“足标代换法”来确定晶体的独立介电常数。

设转动前，晶体的坐标为o-xyz，绕z轴转90°后，晶体的坐标为o-x’y’z’，见图2-10。新旧坐标轴之间的关系为：  x’→y，y’→-x，z’→z

用（1、2、3）来代表（x、y、z）有：

          1→2，2→-1，3→3

所以有：11→22，22→11，33→33，12→-21，13→23，23→-13 

 

与介电常数联系即得：ε‘₁₁=ε₂₂，ε’₂₂=ε₁₁，ε’₃₃=ε₃₃，eε’₁₂=-ε₂₁，ε’₁₃=ε₂₃，ε‘₂₃=-ε₁₃

因为z轴是四次旋转轴，晶体绕z轴转90°后，介电常数应保持不变，即：ε’₁₁=ε₁₁，ε’₂₂=ε₂₂，ε‘₃₃=ε₃₃，ε‘₁₂=ε₁₂，ε‘₁₃=ε₁₃，ε‘₂₃=ε₂₃

比较上述两式结果，可见只有ε₁₁=ε₂₂，ε₁₂=ε₁₂以及ε₁₂=ε₁₃=ε₁₃=ε₂₃=0时，两者才完全一致。

足标代换法 —— 一般过程

点群分析：

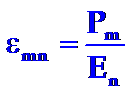
例如—点群4：只有一个4度旋转轴，而且沿c轴，即z轴方向。

足标变化：

绕z轴旋转90°后 ，x→y,y→-x,z→z,

用（1 2 3） 代表 （x y z）

1→2, 2→-1,3→3

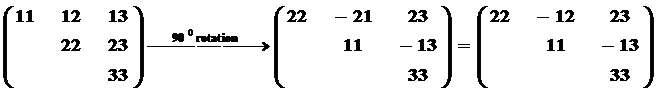
旋转后性质保持不变（对称性的要求）

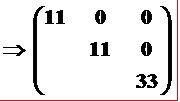 再进行其它的旋转操作不改变介电常数矩阵的形式

足标代换法—例2：mm2点群

铌酸钡钠（Ba₂NaNb₅O₁₅）晶体，镓酸锂（LiGaO₃）晶体都是属于正交晶系mm2点群的晶体。它们的z轴是二次轴，x面、y面是对称面。现在根据它们的对称性质用足标代换法来确定独立的介电常数。

因为晶体的x面是对称面，固有x’→ -x、y’→ -y、z’→ -z，即：1→-1、2→2、3→3，

 

 mm2中的2

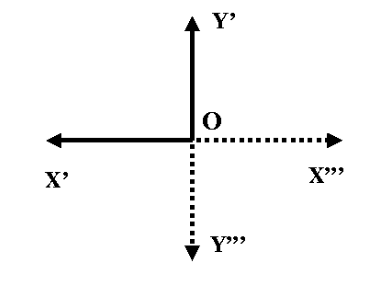
因为晶体的z轴是二次轴，当晶体绕z轴转180°后，有x”→-x’、y”→-y’、z”→z’，即：1→-1、2→-2、3→3，

 

 

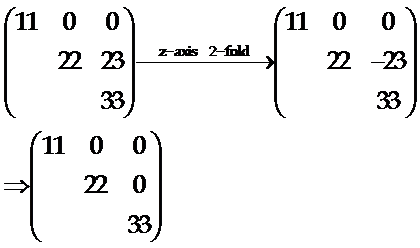
另一个镜面操作不再改变矩阵的形式于是得到mm2点群晶体的介电常数的矩阵形式为：

 

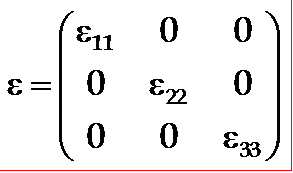
 独立介电常数为ε11、ε22、ε33三个。