◎ 为了得到各向异性介质中极化强度分量(Px、Py、Pz)与电场强度分量(Ex、Ey、Ez)之间的关系式,进行如下实验。当介质在x方向受到电场Ex的作用时,不仅在x方向出现极化强度Px(1),而且在y方向和z方向也出现极化强度分量Py(1)和Pz(1),它们与Ex的关系为:
![]()
◎ 同理,在介质的y、z方向,分别受到电场Ey或Ez的作用时,产生的极化强度分量为:


◎ 当介质受到任意电场E(Ex、Ey、Ez)的作用时,介质中产生的极化强度P(Px、Py、Pz)与E之间的关系为:
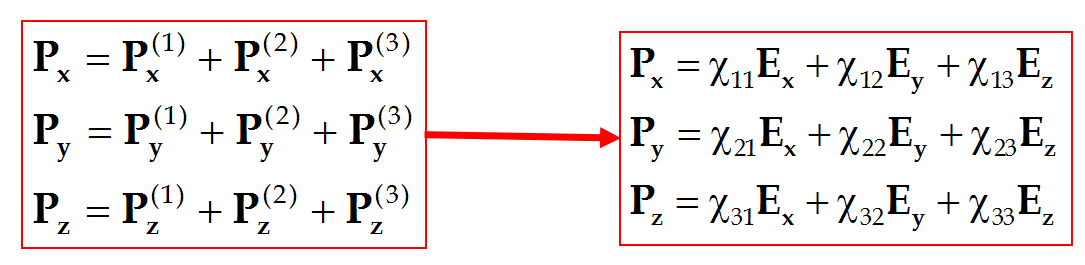
◎ 上式表示各向异性介质中的极化强度分量与电场强度分量之间的关系。实验上还发现,理论上也可以证明,对于所有的介质都存在χ12=χ21,χ13=χ31和χ23=χ32,即独立的极化率系数只有六个。于是上式可改写为:

◎ 由此可见,对于各向异性介质沿x方向的极化强度分量Px不仅与x方向的电场Ex有关,而且与y、z方向电场分量Ey、Ez有关,或者说Px与Ex、Ey、Ez之间存在线性关系。同理,Py、Pz也分别与Ex、Ey、Ez之间存在线性关系。描写电介质材料介电性质的极化率,有六个独立分量(χ11、χ12、χ13、χ23、χ22、χ33)。就是说电介质材料的极化率,即不是标量,也不是矢量,而是二级对称张量,它与E 、P的方向有关。
◎ 为了方便,我们规定x、y、z方向为1、2、3方向,于是(Px、Py、Pz)就可写成(P1、P2、P3),(Ex、Ey、Ez)就可写成(E1、E2、E3)。上式可简化为 :
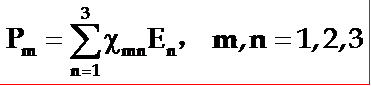
或:

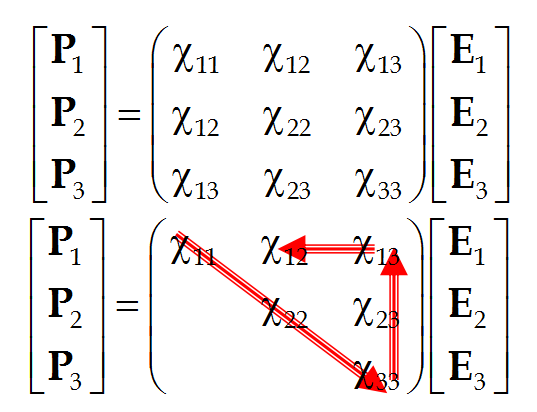
◎ 式中介电常数ε11=(∂Dx/∂Ex)Ey、Ez,为当Ey、Ez保持不变时,Ex改变一个单位时所引起Dx的变化。介电常数ε12=(∂Dx/∂Ey)Ez、Ex,为当Ez、Ex保持不变时,Ey改变一个单位时所引起Dx的变化。其它介电常数的意义与ε11、ε12的类似,介电常数的大小由材料的介电性决定。
◎ 介电常数εmn与极化率χmn之间的关系在x方向上的分量:
![]()
![]()
![]()
同理可得:
![]()
写成矩阵形式为:

(1)不论是各向同性的电介质,还是各向异性电介质,关系式D=ε0E+P都是成立的。
(2)对于各向同性的线性电介质材料,D、E、P的方向相同,并有D=εE,P=χE;ε与χc是标量,与,D、E、P的分量方向无关。ε与χ之间的关系为:ε=ε0+χ。
(3)对于各向异性电介质材料,D、E、P的方向彼此不同。
描写完全各向同性介质,只要一个介电常数,
描写完全各向异性介质,需要六个独立的介电常数。
独立的介电常数的个数与材料的对称性有关,而且一般情况下独立的介电常数的个数是界于一个和六个之间。


