压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
介电性质（八）



 




◎ 从以上讨论可见，一般电介质的极化可以分为：电子位移极化Pe、离子位移极化Pi和固有偶极矩的取向极化Porien三种，即介质的极化强度P可以看成是上述三种贡献的总和，

 

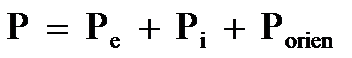
◎ 按照这种看法，可把电介质分为三类：

1. 离子位移极化Pi=0和取向极化Porien=0，但电子位移极化Pe≠0的电介质。

2. 取向极化Porien=0，但电子位移极化和离子位移极化均不等于零，即P=Pe+Pi的电介质。

3. Pe≠0，Pi≠0，Porien≠0，即P=Pe+Pi+Porien的电介质。

◎ 由于固体的结构比较紧密，分子（原子或离子）之间的相互作用较强，洛仑兹有效场Eeff=E+P/3ε0不适用，所以固体有效场的计算通常是一个复杂而且困难的问题。这里只对一些简单的典型固体做一些说明。

一、Pi=Porien=0，但电子位移极化Pe不等于0的电介质

只有Pe≠0的固体电介质大都是属于元素晶体，例如金刚石。设这种固体电介质的有效场为:

其中γ为有效场系数。设单位体积内的原子数为N，则有：

再从




可得

便得到介电常数与电子位移极化率αe关系为

 

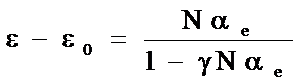
如果有效场系数γ=1/3ε0，则有

   

 

上式就是克劳修斯—莫索提（Clausius-Mossotti）关系式。欲检验上式是否正确，只要测量介电常数ε与单位体积中的原子数N的函数关系。对于气体电介质，容易做到使单位体积中的原子数N发生变化；

对于固体电介质，只能通过改变温度使N发生变化。由于N随温度变化的范围很窄，所以难以用实验检验上两式。

 对于这类元素固体电介质，实验上还发现它们的介电常数ε等于折射率n的平方，即ε=n2。因为在光频范围内，离子位移跟不上电场的迅速变化，所以高频介电常数ε∞只能是电子位移极化的贡献。例如，实验上测得金刚石的介电常数为：




 

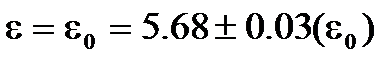
二、Porien=0，P=Pe+Pi的固体电介质

一般说来，没有固有偶极矩的离子晶体，存在电子位移极化和离子位移极化，静态介电常数ε为

 

高频介电常数为：


◎ 对于氯化钠型离子晶体的介电常数ε与ε∞如表2—2所示。从表中可以看出，离子位移极化约为电子位移极化的二到三倍，但是在非离子性固体中，离子位移极化只等于电子位移极化的一个较小的分数。

                                表2-2  碱金属卤化物的静态介电常数e与高频介电常数e

 


◎ 现在讨论一下用一种简单的理论是否能解释e与e¥之间的差别。在外加静电场的作用下，若正负离子分别产生感应偶极矩为P+与P-，正负离子间的相对位移为x。则极化强度为：

◎ 其中N为单位体积中的正离子（或负离子）数。

◎ 设正负离子的有效场相同，则有

 

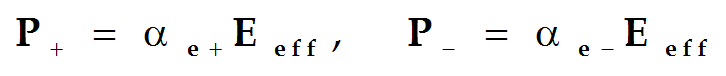
◎ 其中αe+与αe-分别代表正负离子的电子位移极化率。因为离子间的相对位移x由电场力以及准弹性力两者相等所确定，即：

 


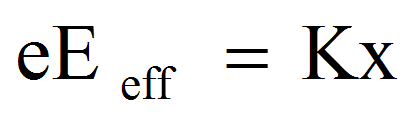
于是得到

 


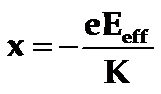
 ◎ 其中K为准弹性常数。可以得到：

 

 


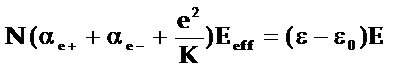
◎ 若洛仑兹有效场


◎ 代入上式即得：

◎ 上式的形式与克劳修斯-莫索提关系类似，只是多了一项离子位移极化的贡献。

◎ 其次，在高频时，介电常数ε完全是电子位移极化的贡献，因此有


 



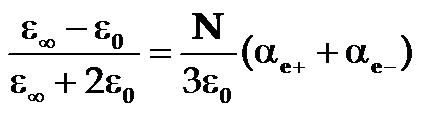
◎ 进一步可得：


 

◎ 通过压缩模量的数据可求得准弹性常数K，再通过介电常数ε和ε0的测量，可验证上）式是否成立。实验结果表明ε和ε0之间的关系不能很好地满足上式，就是说洛仑兹有效场Eeff=E+P/3ε0不能正确地反映离子晶体中的有效场。

◎ 有人考虑到正负离子的有效场不同，得到如下关系式：

 

◎ 上式与实验结果符合得更好一些。可见，有效场的选择是很重要的。

 

 

 

◎ 存在固有偶极矩的固体电介质其极化强度为

◎ 这种电介质没有定量的理论，也没有关于介电常数的简单公式。

◎ 因为它存在计算内场的困难；其次，不同于气体和液体电介质，固体电介质中的固有偶极矩不易转向。这里只介绍一两个简单的现象。

 

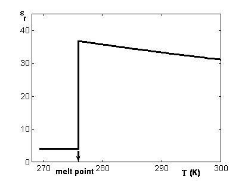
◎ 如下图给出了亚硝基苯C6H5NO2的介电常数与温度的关系。从这个结果可以看出，在熔点附近，介电常数急剧增加。这表明亚硝基苯在固态时，其固有偶极矩不能自由转动，Porien基本上等于零。在液态时，固有偶极矩可以沿电场方向取向排列，所以介电常数急剧增加是取向极化的贡献。之后，随着温度上升，热运动的无序效应增加，介电常数因之逐渐减小。

 

 

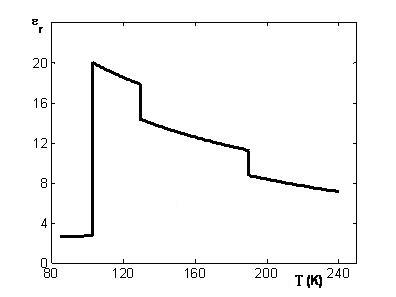
◎ 下图给出了硫化氢H2S的介电常数与温度的关系。H2S的熔点为103.5K。从图中看出，H2S的情况比亚硝基苯更为复杂。在103.5K以下，固有偶极矩被“冻结”；在103.5K晶体结构发生了某中变化，使固有偶极矩可以自由转动，所以介电常数急剧增加。当温度上升时，热运动的无序效应使得介电常数减小。图中介电常数另外两个突然下降，可能是由于发生相变时，单位体积内的分子数变小而引起的结果。

 



◎ 极化机制->极化率->极化强度

◎ 有效场的引入->极化强度->介电常数

◎ 虽然有了很多概念，但存在很大的问题：固体的介电常数的计算还没有比较准确的方法；这与其相互作用复杂有很大的关系。

◎ 这里介绍的只是线性介质的静态介电常数；

◎ 有关动态介电常数和铁电体的介电常数相关内容，以后还要介绍。