◎ 计算Eout时，可以利用球外介质可看成连续介质的条件，而把球外分子对球心的作用，用宏观方法处理。就是说，将球挖空后，可把球外分子对球心的作用，看成是空心球表面的极化电荷对球心分子的作用。空心球表面的极化电荷在球心产生的电场Eout的计算方法如下：
计算空球表面电荷在球心产生的电场示意图
◎ 因为空心球中心的电场等于球面上的电荷在球心产生的电场强度的矢量和。该球面的面电荷为s，则环形面积元dA=2πrsin(θ)rdθ上的电荷为：
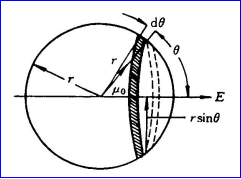
◎ 如图所示，环形面积元上的电荷在球心产生的电场强度分布在球心的圆锥面上，它们在外电场方向上的分量矢量和为：
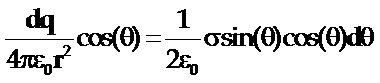
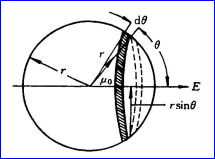
◎ 关于Ein=? 因为球内介质不能看成是连续的，所以计算Ein时，就需要考虑到介质的微观结构。例如气体电介质，由于气体分子可以自由地到达容器内各个地方，因此气体分子在容器内的分布是各向同性的，当然在球内也是各向同性的。
根据气体分子的各向同性就可得到球内各气体分子的偶极矩在球心处产生的电场强度的矢量和为零。
即对气体电介质有：
◎ 又如：对于同样原子组成的简立方晶体、体心立方晶体或面心立方晶体，它们是对称性最高的晶体，根据这些晶体的对称性，也可以得到球内各原子的偶极矩在球心处产生的电场强度的矢量和为零。即对于简单立方、体心立方和面心立方等晶体也有：
◎ 所以气体电介质以及简单立方、体心立方和面心立方等晶体电介质的洛仑兹有效场为：
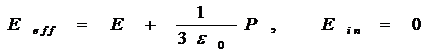
或：
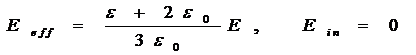
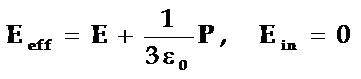
◎ 上两式简称为洛仑兹有效场表达式，从这个表达式可以看出洛仑兹有效场Eeff总是大于介质的外电场E。
◎ 应该注意：不是所有的立方晶系都能得到的Ein =0结论。例如在居里温度以上钛酸钡晶体是属于立方晶系，但是在钛酸钡晶体中，氧离子周围并不是立方对称性的，因而不能使用Ein =0。
◎ 如何计算Ein ≠0，因为球内介质不能看成是连续的，所以计算球内各分子的偶极矩在球心处产生的电场时，需要计入各分子的贡献。
◎ 具体做法是：先求其中一个分子（例如第i个分子）的偶极矩在球心产生的电势，再利用电场强度与电势之间的关系求得（Ein）i，最后对球内所有分子（除去球心分子）求和，即可得到的Ein表达式。
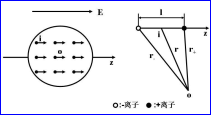
◎ 设外电场的方向与晶体的z轴平行，如图所示。第i个分子的偶极矩在球心处产生的电势为：
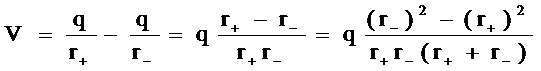
◎ 其中r+与r-为第i个分子的正负电荷中心到球心的距离。若r为第i个分子的偶极矩中心到球心的距离，l为第i个分子正负电荷中心之间的距离，l与z平行则从图中容易得到：
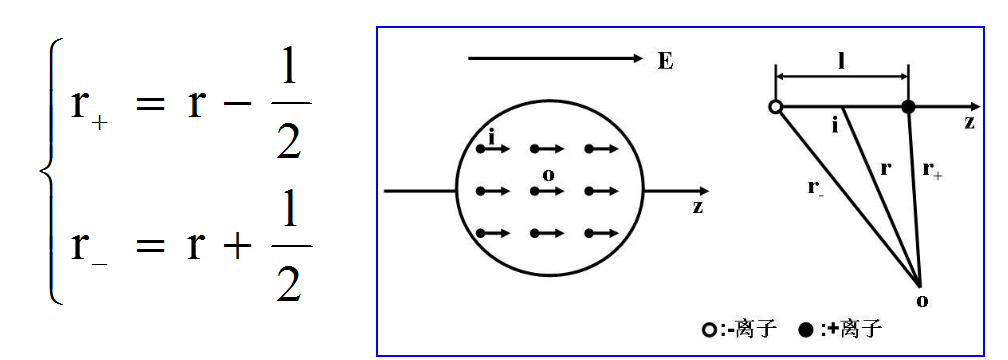
或者：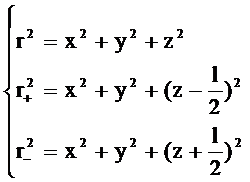 
注意到l<<r条件，即得：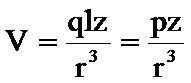
◎ 其中p=ql为第i个分子的偶极矩，若用足标i表示出第i个分子在球心产生的电势，则为：
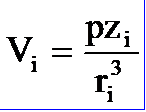
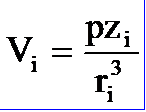
◎ 利用电场与电势的关系式，即可求得球内第个分子的偶极矩作用在球心的电场强度（Ein）i的分量为：
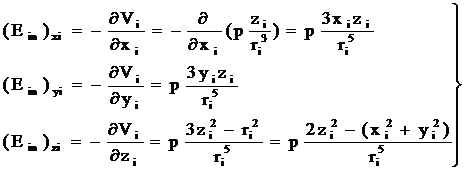
◎ 球内其它分子作用在球心的电场强度的形式与上式相同。所以将上式对球内所有分子（除去球心分子）求和，即得球内其它分子在球心产生的电场为：
◎ 若作用在介质中的外电场为E（Ex、Ey、Ez），第i个分子的偶极矩为Pi（Pxi、Pyi、Pzi），在此情况下，球内其它分子在球心处产生的电场为：
◎ 以相同原子组成的简单立方晶体为例，若在外电场方向与简单立方晶体的z轴平行，利用简单立方晶体的的对称性可以得到：
◎ 以及
◎ 即得（Ein）x=（Ein）y=（Ein）z=0，或者Ein=0。
◎ 同样，对体心立方、面心立方等晶体，计算Ein时，应该从上式开始。
◎ 对于由不同原子（或离子）组成的的晶体，因为不同原子（或离子）的周围情况不同，作用在不同原子（或离子）的有效场也不同。不同原子上的有效场，可以近似写成：
◎ 其中γ1、γ2、…成为内场系数。只有当Ein=0时，才能得到γ=1/3ε0，上式也称为洛仑兹有效场表达式。
◎ 应该注意：上述讨论中，把感应偶极矩看成是“点”偶极矩，并认为有效场是均匀的。实际上，离开中心原子几个原子的距离（即几个10-8厘米）范围的原子所产生的电场远非均匀的，所以洛仑兹有效场与实际上的有效场是有差距的。其次洛仑兹有效场只能近似地用于电子或离子位移极化的问题中。
