压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
介电性质（六）



◎ 用介质极化的三种机制，讨论气体的介电常数，可得到满意的结果。

但是在固体和液体电介质中，情况就比较复杂。因为在固体和液体电介质中，分子之间的距离较小，分子之间的相互作用不能忽略不计。

偶极子阵列 


 


每个偶极子本身产生电场，偶极子之间会相互影响


 


                                                       

 

有效场理论

◎ 作用在固体（或液体）某分子上的电场，除了外电场外，还应计入其它分子的偶极矩所产生的电场的作用。就是说作用在固体（或液体）某分子上的电场与外电场不同，称为介质中的有效场，或简称内场，常用记号E内或Eeff表示。

这一节主要讨论如何计算有效场，以及对材料介电常数的影响。

◎ 作用在电介质中某分子上的有效场是两个电场的叠加，其一为介质中的外电场；另一为其它极化分子作用在所考虑的分子上的电场。

◎ 因为偶极矩之间的相互作用是长程力，一般电介质的结构又比较复杂，所以要严格算出有效场是很困难的，现有的各种计算有效场的方法都作了不同程度的近似。

◎ Lorenz Effective Field:

◎ 通常用的较多的是洛仑兹有效场（或洛仑兹内场）。

◎ 以充有电介质的平行板电容器为例，如图所示。介质中的外电场强度为：

 

 

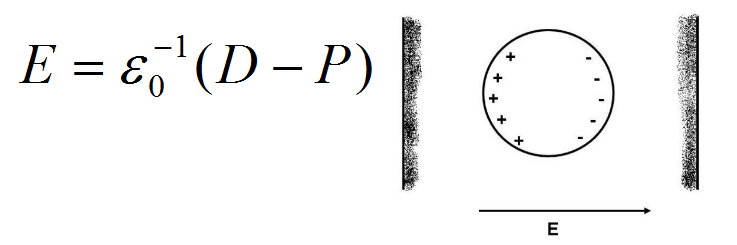
◎ 为了计算有效场，洛仑兹把介质中各分子对所考察分子的作用划分为两部分，即近邻分子对该分子的作用，和其它较远分子对该分子的作用。具体做法是：在介质中，想象地挖出一个圆球，如图所示，球心为考察分子的位置，球的半径r要求远大于分子半径（例如大几百倍），可以将球外的介质看成连续的;微观无限大，宏观无限小


◎ 另一方面，球的半径与整个介质比又是很小的。当想象地挖出此球时，不会引起介质中的电场发生变化。作出上述考虑后，作用在球心分子上的有效场就可以认为是：介质中的电场E，外分子作用在球心分子的电场Eout与球内其它分子作用在球心分子的电场Ein之和，即：

 

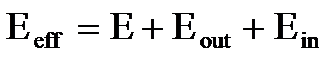
现在问题是如何计算Ein与Eout？