压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
介电性质（五）


 










 

 

 


◎ 常见的三种极化机制：电子位移、离子位移和固有偶极矩取向极化；

◎ 电子位移极化、离子位移极化产生的极化率较小且与温度无关；

◎ 固有偶极矩取向极化产生的极化率较大，但随温度升高而减小。

 

 

◎ 电子位移极化和离子位移极化不随温度变化的前提：

◎ 电子在温度改变时没有热激发；

◎ 晶格常数（离子之间的距离）不随温度变化；或者说没有热胀冷缩；

 

◎ 以上讨论的极化率是孤立单元（原子的电子位移，离子对的离子位移，没有相互作用的固有偶极子）的极化率，并不是材料的极化率。

 

◎ 材料的介电常数与三种极化机制之间的关系，有效场理论；

◎ Clausius-Mossotti关系；

◎ 知道电介质极化的三种微观机制后，就可以对电介质的静态介电常数提出一个微观解释。最简单的情况是分子之间的相互作用可以忽略不计。例如，较稀疏的气体，分子之间距离较大，因此分子之间的相互作用可以忽略不计。在这种情况下，作用在分子上使分子极化的电场就等于介质中的外电场E。

◎ 设单位体积内气体分子数为N，介质的极化强度P就是上述三种极化机制的贡献总和，即：

 

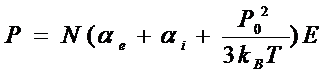
◎ 这里假设：分子数目和离子对数目和固有偶极矩数目相同；外加电场与没有分子所感受到得电场相同。

◎ 再通过气体的静态介电常数e与极化强度和电场强度之间的关系e-e0=P/E，即得气体的静态介电常数为：

 

 

◎ 以上表达式假设材料同时存在三种极化机制。

 

 

◎ 例子：右图给出了某些气体有机物质的介电常数与温度的关系，这些结果与上式基本符合。

 

 

◎ 从图可以看出：CC14和CH4的介电常数与温度无关，这表明CC14和CH4分子没有固有偶极矩，分子具有对称性结构。CHC13、CH2C12和CH3C1的介电常数与温度有关，通过这些直线的斜率以及单位体积内的分子数N，即可得分子的固有偶极矩P0；再通过这些直线的延长线与纵坐标的交点，即可得到位移极化率（αe+αi）。因为CHC13、CH2C12和CH3C1分子存在固有偶极矩，所以这些分子具有非对称结构。