
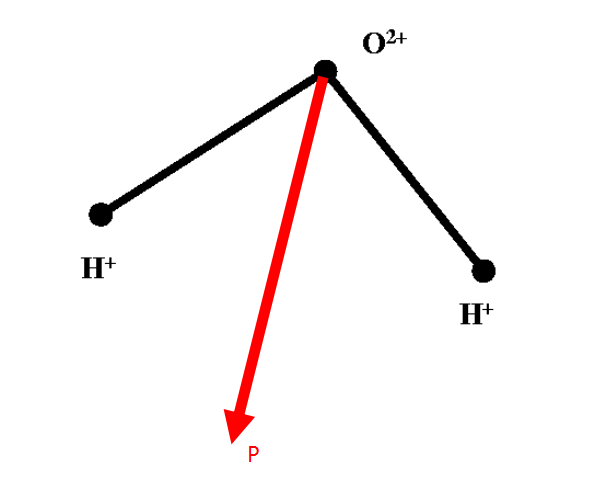
◎ 如果组成介质的分子具有固有偶极矩(称为有极分子),例如,水分子H2O,其中氧离子与二个氢离子不是在一条直线上,而是分布在三角形的三个顶点上。因此水分子的正负电荷中心不重合,存在固有偶极矩,如图所示。
◎ 当电场 E=0时,介质中各分子的固有偶极矩的取向是无规则的,所以各偶极矩的矢量和为零,介质不存在极化。当电场 E≠0时,在电场作用下,这些固有偶极矩将沿着电场方向排列,各偶极矩的矢量和不为零,介质产生极化。在离子位移极化和电子位移极化的情况,位移极化的产生是由于电场力与弹性力的共同作用下出现与电场方向平行的感应偶极矩。
◎ 电场力的作用是使正负电荷中心分离,准弹性力的作用是使正负电荷中心重合,即准弹性力起着阻碍极化的作用。电场力与准弹性力是矛盾的两个方面。
在取向极化的情况中,电场的作用是使分子的固有偶极矩转到沿电场的方向排列;而妨碍定向排列的阻力是介质中分子的热运动。
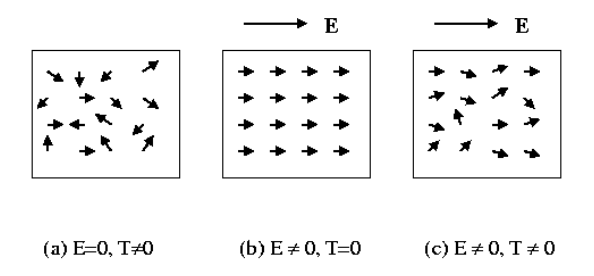
◎ 因为当温度不等于绝对零度 (即T≠0K)时,介质中各分子的热运动也不等于零,所以在一般电场作用下,介质中各分子的固有偶极矩是不能出现如图所示的完全有序化,这也表示当E=0,T≠0K时,各分子的固有偶极矩在电场方向上的分量各不相同,而固有偶极矩在电场方向上的分量才对介质的极化有贡献。
◎ 计算结果,可得取向极化率αorien为:
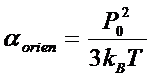
式中为P0分子固有偶极矩,kB是玻尔兹曼常数,T是绝对温度。
◎ 可以看出,取向极化率不同于位移极化率,取向极化率与温度有关,而位移极化率与温度无关。
◎ 取向极化率αorien大小的估计。
◎ 室温时,P02 ~10-34cgs·厘米,3kBT~12×10-14尔格;
故得αorien≌10-21(厘米)3,
◎ 而位移极化率的大小为10-24(厘米)3。
◎ 可见,取向极化率远大于位移极化率。
◎ 如果介质极化时存在上述三种极化机制,其中以取向极化的贡献最大。分子中存在固有偶极矩的概念的建立,不仅可以解释一些由有极分子组成的电介质具有较大的介电常数这一事实,而且对于电介质的了解和有关的分子结构知识都是有贡献的。
◎ 取向极化率αorien的导出
◎ 因为介质中的分子总数是非常多的。例如,一个摩尔体积的介质中就包含6×1023个分子,这6×1023个分子并不是固定不动的,而是在做热运动。热运动的规律不同于机械运动规律,因此用力学方法来确定每个分子的固有偶极矩在电场方向上的分量是根本无法实现的。但是用统计的方法,是能够确定各分子的固有偶极矩在电场方向上的平均值。
◎ 下面就介绍如何用统计物理学的方法来确定:电场为E,温度为T时,分子的固有偶极矩在电场方向上的分量平均值。
设分子间的相互作用可以忽略不计,某个分子的固有偶极矩P0与电场E的夹角为θ,如图所示。
电场中偶极子示意图
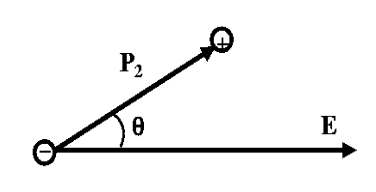
因此偶极矩在电场方向上的分量为
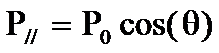
势能为:
![]()
经典统计分布-玻尔兹曼(Boltzmann)统计分布:
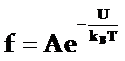
A为比例系数,kB为玻尔兹曼常数,kB=1.38×10-16尔格/度
对比量子统计:

![]()
![]()
用dN代表固有偶极矩P0与电场E的夹角介于θ→θ+dθ之间的偶极分子数目。按照统计物理有
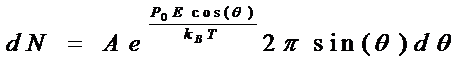
![]()
![]()
这样dN个分子的固有偶极矩在电场方向的分量为:
![]()
固有偶极矩在电场方向上的平均分量为:
即:![]()
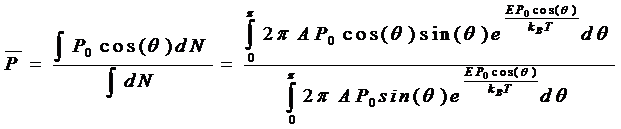
令:
![]()
可得:

其中:L(β)称之为朗之万(Langevin)函数。
朗之万(Langevin)函数
Langevin function L(β)
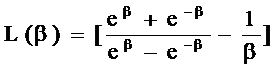
考虑三种情况
![]()
(1) 当β>>1时,即电场很强,温度很低时,利用:
![]()
得: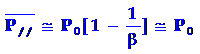
这表明电场E很大,温度T很低时,固有偶极矩几乎完全转到电场方向,所以固有偶极矩在电场方向的平均值等于固有偶极矩。
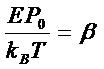
(2)
当b<<1时,即P0E<<kBT时,利用:
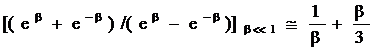
得:![]()
这表明当P0E<<kBT时,固有偶极矩在电场方向上的分量平均值与电场E成正比,与温度T成反比。电场增大,P也增大;温度升高,P则减小。
下面估计一下室温时E多大才能满足P0E<<kBT的条件。室温时kBT=1.38×10-16×300=4×10-14尔格,固有偶极矩P0=e(r++r-)≈4.8×10-10×2×10-8 = 9.6×10-8 = 10-17cgs单位。对于P0E/kBT=1的电场为:
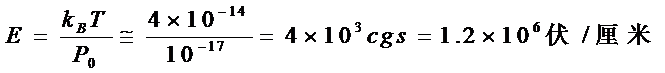
由此可以看出室温时,电场E=103伏/厘米仍能满足P0E<<kBT的条件。就是说在通常条件下,可以使用β<<1的条件。
朗之万函数L(β)与β的关系示意图
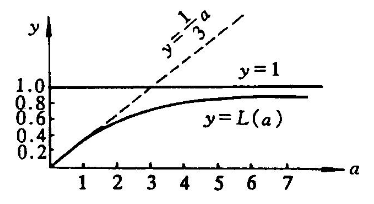
(3) 在一般情况下,L(β)与β的函数关系如图所示, 可以看出:
当β>>1时,L(β)≈1;
当β<<1时,L(β)的斜率为1/3。


