压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
晶体结构（九）





◎ 采用国际符号，不仅可以表示出各种晶类中有那些对称元素，而且还能表示出这些对称元素在空间的方向。国际符号根据各种晶类的对称性可以是三项、或二项、或一项符号组成，它分别表示晶体某三个、或二个、或一个方向上的对称元素。如果在某一个方向上，同时具有对称轴和垂直于此轴的对称面，则写成分数形式。




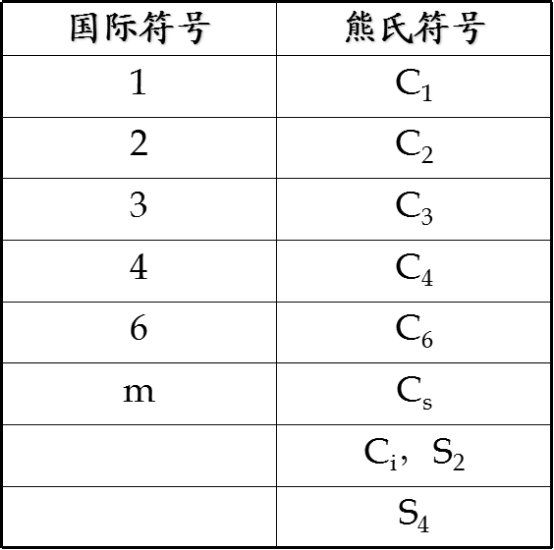
◎ Cn：字母表示旋转的意思，组标n表示旋转的次数，n=1、2、3、4、6。例如C2代表二次旋转轴。

◎ Cnh：表示除了n次旋转轴外，还包括一个与此轴垂直的对称面。2/m、 4/m、6/m

◎ Cnv：表示除了n次旋转轴外，还包括一个与此轴重合（即平行）的对称面。2mm 、4mm、3m、6mm


◎ Cni：表示除了n次旋转轴外，还包括一个对称中心。


◎ Ci：表示有一个对称中心。


◎ S4：表示有一个四次旋转倒反轴。

◎ Dn：表示除了n次主旋转轴外，还包括n个与之轴垂直的二次旋转轴。222、32、422、622 

◎ Dnh：表示除了Dn的对称性外，还包括一个与主旋转轴垂直的对称面，和n个与二
次旋转轴重合（即平行）的对称面。 mmm、4/mmm、6/mmm


◎ Dnd：表示除了Dn的对称性外，还包括n个平分两个二次旋转轴夹角的对称面。

◎ T：除了四个三次旋转轴外，还包括三个正交的二次旋转轴。 23

◎ Th：除了T的对称性外，还包括与二次旋转轴垂直的三个对称面。 m3


◎ Td：除了T的对称性外，还包括六个平分两个二次旋转轴夹角的对称面。

◎ O：包括三个互相垂直的四次旋转轴，六个二次旋转轴，和四个三次旋转轴。 432

◎ Oh：除了O的对称性外，还包括Td与Th的对称面。 m3m








◎ 由于分子没有无限周期性的限制，所以分子点群的数目要多于晶体中的点群数目32个

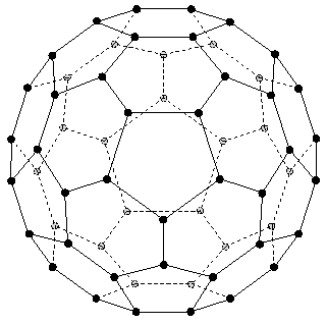
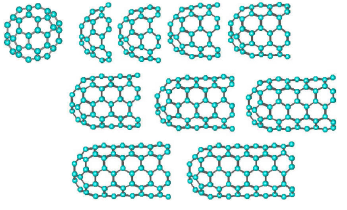
◎ 自然界对称性很多，例如：五度对称性，足球，富勒烯C60, buckministerfullerence，碳管





◎ 对称元素和对称操作

◎ 晶体的三十二个点群

◎ 对称性和点群对于压电铁电体非常重要！

◎ 只有晶体才会有压电铁电性，不存在非晶压电铁电体。但是有非晶半导体和非晶磁性材料。




      ◎ 由于无限大周期性的限制，晶体中的对称操作只能有：1，2，3，4，6，i，m,  ；


◎ 由这些对称操作所构成的集合就是晶体中的点群；

◎ 点：所有这些对称操作下，肯定有一个点是不变的；

◎ 晶体中一共有32个这样的点群；