压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
晶体结构(四)




◎ 晶体的对称性是由其内部格子结构所决定的。它不仅与晶体的结构有密切关系，而且也于晶体的力学、电学、光学以及压电铁电性质等有密切关系。

◎ 可以说，晶体的对称性是晶体分类的基础，也是研究晶体其它性质的基础。

◎ 这里先主要介绍的对称性，不包括平移对称性在内，所以是宏观对称性。

◎ 晶体结构本身具有对称性，x-射线衍射

◎ 晶体的物理性质与对称性有关，介电常数，压电常数等…

◎ 研究方便：立方晶体ε11=ε22=ε33，其它εij=0

◎ 计算方便：简化计算，量子化学计算

◎ 能使对称图形复原的动作称为对称操作，例如，前面提到的对称轴的旋转，对称面的反映，此外，对称中心点的反演（或倒反）等，都是对称操作。Operation

◎ 进行对称操作时，还必须依赖于一定的几何元素，如对称中心、对称面、对称轴等，这些几何元素又称为对称元素。Element


点群符号

              

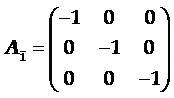
基元=Ax基元

矢量物性=Ax矢量物性

◎ 对称面（镜面）:为一假想平面，相应的对称操作为对此平面的反映。对称面将图形分为镜像反映的两个相等的部分。如下图表示通过对称面m把M反映到M’。对称面在图形上常用双线或粗线表示，国际符号为“m”。 


          m法线//x轴

         



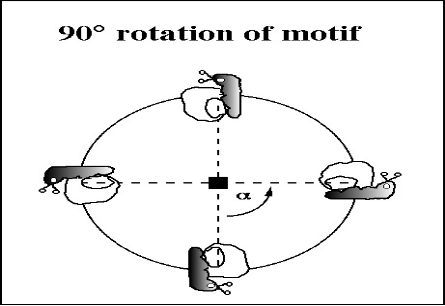
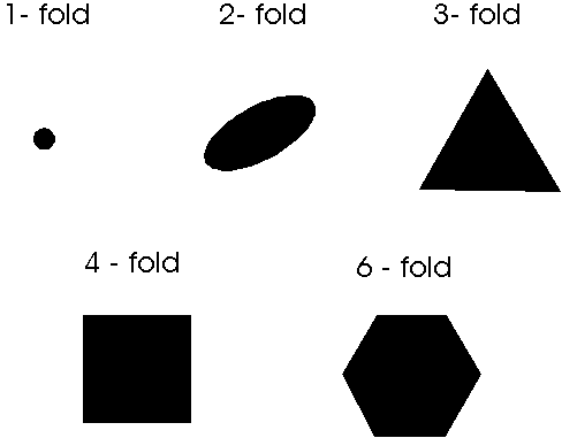
◎ 旋转轴（对称轴）：为一假想直线，相应的对称操作为对此轴线的旋转。一个晶体如绕此轴旋转360°/n后，能够复原，则称此晶体具有n次旋转轴或简称n次轴。由于晶体结构的周期性（即晶体的平移对称性）给晶体的转动对称性带来了严格的限制，即n只能等于1、2、3、4、6，或者说晶体只可能具有1、2、3、4、6次旋转轴，不可能具有5次或高于6次的旋转轴。

            

       旋转轴//z轴

    

         

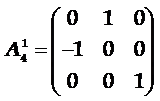
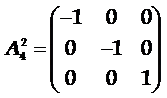
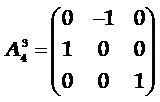
旋转轴符号




◎ 旋转倒反轴（像转轴）：这是一个复合对称元素。它是一个假象的直线和此直线上的一个定点，相应的对称操作为对此轴线转2p/n角度后，接着再对此点进行到反。若晶体经过这个操作后能够复原，则称此晶体有n次旋转倒反轴。Rotation-inversion

◎ 与旋转轴的情况一样，晶体也只能有1、2、3、4、6次旋转倒反轴，而不能有5次或6次以上的旋转倒反轴。旋转倒反轴的国际符号为。

                                

             


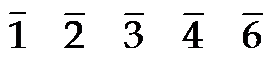
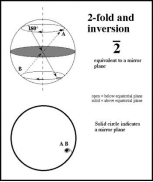
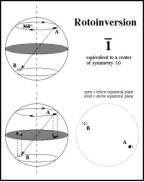
旋转轴//z轴

                 


 

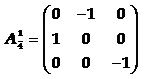
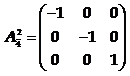
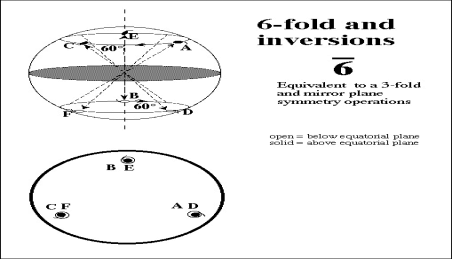
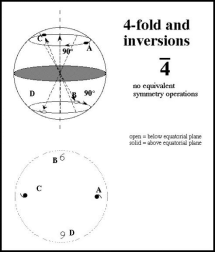
◎ 知道了晶体的八个基本的宏观对称元素后，下一个问题就是：在晶体中，究竟有哪些对称元素和对称操作可以同时存在？它们的组合方式有多少种？在数学上，把对称元素（或对称操作）的集合叫做“对称群”。因为上述对称元素中，不包括平移对称性，进行对称操作时总是有一点保持不动，所以只包括上述对称元素的集合叫做“点群”。