压电铁电

王春雷

目录

  • 1 压电铁电物理 绪论
    • 1.1 绪论(上)
    • 1.2 绪论(下)
  • 2 晶体结构
    • 2.1 晶体结构(一)
    • 2.2 晶体结构(二)
    • 2.3 晶体结构(三)
    • 2.4 晶体结构(四)
    • 2.5 晶体结构(五)
    • 2.6 晶体结构(六)
    • 2.7 晶体结构（七）
    • 2.8 晶体结构（八）
    • 2.9 晶体结构（九）
    • 2.10 晶体结构（十）
    • 2.11 晶体结构（十一）
    • 2.12 晶体结构（十二）
    • 2.13 晶体结构（十三）
  • 3 介电性质
    • 3.1 介电性质（一）
    • 3.2 介电性质（二）
    • 3.3 介电性质（三）
    • 3.4 介电性质（四）
    • 3.5 介电性质（五）
    • 3.6 介电性质（六）
    • 3.7 介电性质（七）
    • 3.8 介电性质（八）
    • 3.9 介电性质（九）
    • 3.10 介电性质（十）
    • 3.11 介电性质（十一）
    • 3.12 介电性质（十二）
    • 3.13 介电性质（十三）
    • 3.14 介电性质（十四）
  • 4 晶体的弹性性质
    • 4.1 晶体的弹性性质（一）
    • 4.2 晶体的弹性性质（二）
    • 4.3 晶体的弹性性质（三）
    • 4.4 晶体的弹性性质（四）
    • 4.5 晶体的弹性性质（五）
    • 4.6 晶体的弹性性质（六）
    • 4.7 晶体的弹性性质（七）
  • 5 压电效应与压电方程组
    • 5.1 压电效应与压电方程组（一）
    • 5.2 压电效应与压电方程组（二）
    • 5.3 压电效应与压电方程组（三）
    • 5.4 压电效应与压电方程组（四）
    • 5.5 压电效应与压电方程组（五）
    • 5.6 压电效应与压电方程组（六）
    • 5.7 压电效应与压电方程组（七）
    • 5.8 压电效应与压电方程组（八）
    • 5.9 压电效应与压电方程组（九）
    • 5.10 压电效应与压电方程组（十）
    • 5.11 压电效应与压电方程组（十一）
    • 5.12 压电效应与压电方程组（十二）
    • 5.13 压电效应与压电方程组（十三）
    • 5.14 压电效应与压电方程组（十四）
    • 5.15 压电效应与压电方程组（十五）
    • 5.16 压电效应与压电方程组（十六）
    • 5.17 压电效应与压电方程组（十七）
    • 5.18 压电效应与压电方程组（十八）
    • 5.19 压电效应与压电方程组（十九）
    • 5.20 压电效应与压电方程组（二十）
    • 5.21 压电效应与压电方程组（二十一）
  • 6 压电振子的振动模式
    • 6.1 压电振子的振动模式（一）
    • 6.2 压电振子的振动模式（二）
    • 6.3 压电振子的振动模式（三）
    • 6.4 压电振子的振动模式（四）
    • 6.5 压电振子的振动模式（五）
    • 6.6 压电振子的振动模式（六）
    • 6.7 压电振子的振动模式（七）
    • 6.8 压电振子的振动模式（八）
    • 6.9 压电振子的振动模式（九）
    • 6.10 压电振子的振动模式（十）
    • 6.11 压电振子的振动模式（十一）
    • 6.12 压电振子的振动模式（十二）
    • 6.13 压电振子的振动模式（十三）
    • 6.14 压电振子的振动模式（十四）
    • 6.15 压电振子的振动模式（十五）
    • 6.16 压电振子的振动模式（十六）
    • 6.17 压电振子的振动模式（十七）
    • 6.18 压电振子的振动模式（十八）
    • 6.19 压电振子的振动模式（十九）
    • 6.20 压电振子的振动模式（二十）
晶体结构(三)





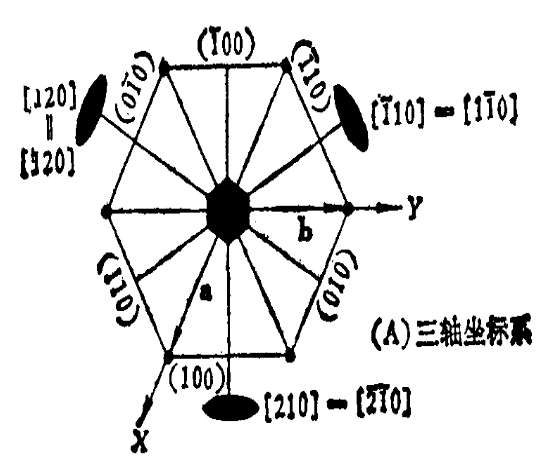
◎ Body-centered-cubic

◎ 每个原胞有2格点





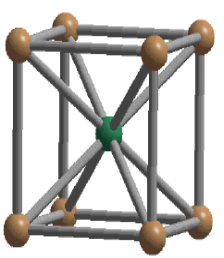
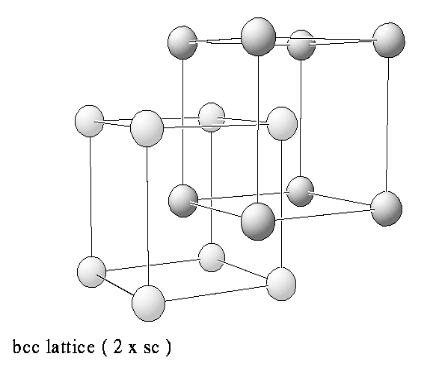
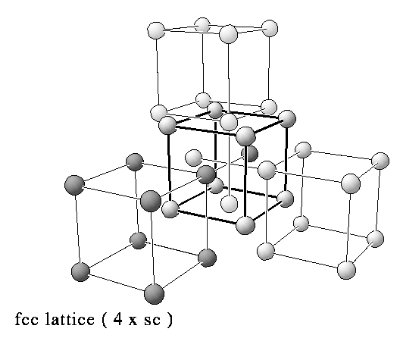
◎ face-centered-cubic

◎ 每个原胞有4格点

 



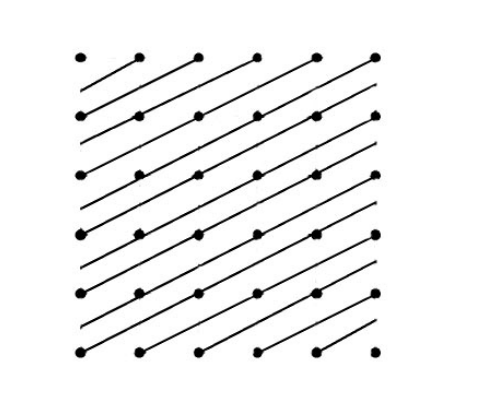
◎ 由于晶体结构的周期性，晶格中各格点的周围情况都是一样的，因此通过任意两个格点作一条直线，则在直线上所有格点的周期相同，这样的直线称为晶棱。再通过其它格点还可以做许多与此晶棱平行的直线，这些平行直线组成一个晶棱族。同一晶棱的方向相同，而且能把所有点子包括无遗 。

               



   ◎ 取格点O为原点，a、b、c为晶胞的三个基矢，则其它任一格点A的位置矢量为

                           

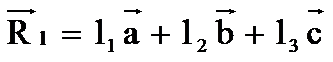
式中11、12、13为整数（或有理数）。取11、12、13的互质比，即11:12:13来表示晶棱OA的方向，通常不直接用比例记号，该用[111213]记号表示之。





 ◎ 晶格中，还可以从各个方向上划分成无限多平面族，即晶面族，如图所示。一族晶面中，彼此距离相等，方向相同，格点在晶面上的分布也相同。从立体几何中知道，要描述一个平面的方向，就是表示出这个平面在三个坐标轴上的截距，描写晶面方向的方法也是如此。

          




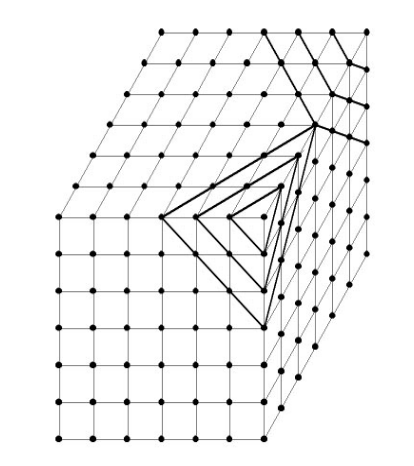
◎ 为了避免使用无限大，常采用截距倒数的互质整数比，即用:

                                       

   来表示晶面的方向。通常不用比例记号，改用（hkl）记号来表示晶面的方向。（hkl）称为晶面指数，或称为米勒（Miller）指数。



◎ 以上所讨论的表示晶向和晶面的方法，对于所有的的晶体都适用。

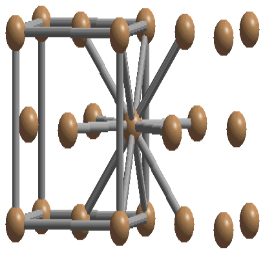
◎ 但是在六角晶系中，如果仍采用三个基矢a、b、c（如下图所示）的方法，则很难反映出六角晶系的对称性，给工作带来不方便。

◎ 因此在结晶学中，往往采用专为六角晶系而设立的按四个晶轴的定向方法，晶向和晶面指数都是用四个指数。