算法的概念

所谓算法，是指为了解决一个问题而采取的方法和步骤。当利用计算机来解决一个具体问题时，也要首先确定算法。

例如，输入三个数，然后输出其中最大的数。将三个数依次输入到变量Ａ、B、C中，设变量MAX存放最大数。其算法如下：

①输入A、B、C；

②A与B中较大的一个放入MAX中；

③把C与MAX中较大的一个放入MAX中。

再如，输入10个数，打印输出其中最大的数。算法设计如下：

①输入1个数，存入变量A中，将记录数据个数的变量N赋值为1，即N=1；

②将A存入表示最大值的变量Max中，即Max=A；

③再输入一个值给A，如果A>Max， 则 Max=A， 否则Max不变；

④让记录数据个数的变量增加1，即N=N+1；

⑤判断N是否小于10，若成立则转到第（3）步执行，否则转到第（6）步；

⑥打印输出max。

利用计算机解决问题，实际上也包括了设计算法和实现算法两部分工作。首先设计出解决问题的算法，然后根据算法的步骤，利用程序设计语言编写出程序，在计算机上调试运行，得出结果，最终实现算法。可以这样说，算法是程序设计的灵魂，而程序设计语言是表达算法的形式。

算法的特征

（1）有穷性（Finiteness）

算法的有穷性是指算法必须能在执行有限个步骤之后终止。

（2）确定性（Definiteness）

算法的每一步骤必须有确切的定义。

（3）输入项（Input）

一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输入是指算法本身定出了初始条件。

（4）输出项(Output)

一个算法有一个或多个输出，以反映对输入数据加工后的结果。没有输出的算法是毫无意义的。

（5）可行性(Effectiveness)

算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步，即每个计算步都可以在有限时间内完成（也称之为有效性）。

算法的评价

同一问题可用不同算法解决，而一个算法的质量优劣将影响到算法乃至程序的效率。算法分析的目的在于选择合适算法和改进算法。一个算法的评价主要从时间复杂度和空间复杂度来考虑。

（1）时间复杂度

算法的时间复杂度是指执行算法所需要的时间。一般来说，计算机算法是问题规模n 的函数f(n)，算法的时间复杂度也因此记做T(n)。

T(n)=Ο(f(n))

因此，问题的规模n 越大，算法执行的时间的增长率与f(n) 的增长率正相关，称作渐进时间复杂度（Asymptotic Time Complexity）。

例如顺序查找平均查找次数(n+1)/2，它的时间复杂度为O(n)，二分查找算法的时间复杂度为O(logn)，插入排序、冒泡排序、选择排序的算法时间复杂度上O(n2 )。

（2）空间复杂度

算法的空间复杂度是指算法需要消耗的内存空间。其计算和表示方法与时间复杂度类似，一般都用复杂度的渐近性来表示。同时间复杂度相比，空间复杂度的分析要简单得多。

算法的描述（表示方法）

1．自然语言

用中文或英文等自然语言描述算法。但容易产生歧义性，在程序设计中一般不用自然语言表示算法。

2．流程图

流程图由一些特定意义的图形、流程线及简要的文字说明构成，它能清晰明确地表示程序的运行过程，传统流程图由以下图形组成：

（1）起止框：说明程序起点和结束点。

（2）输入/输出图框：输入输出操作步骤写在这种框中。

（3）处理框图：算法大部分操作写在此框图中。

（4）菱形框代表条件判断以决定如何执行后面的操作。

例如网上购物的流程图：

3．N-S图

在使用过程中，人们发现流程线不一定是必需的，为此人们设计了一种新的流程图——N-S图，它是较为理想的一种方式，它是1973年由美国学者I.Nassi和B.Shneiderman提出的。在这种流程图中，全部算法写在一个大矩形框内，该框中还可以包含一些从属于它的小矩形框。例如网上购物的N-S图见图7.6。N-S图可以实现传统流程图功能。

注意：在N-S图中，基本元素框在流程图中的上下顺序就是执行时的顺序，程序在执行时，也按照从上到下的顺序进行。

对初学者来说，先画出流程图很有必要，根据流程图编程序，会避免不必要的逻辑错误。

4．伪代码

伪代码是用介于自然语言和计算机语言之间的文字和符号来描述算法，即计算机程序设计语言中具有的关键字用英文表示，其他的可用汉字，也可用英文，只要便于书写和阅读就可。例如：

if x is positive

then

   print x

else

   print -x

它像一个英文句子一样好懂。用伪代码写算法并无固定的、严格的语法规则，只需把意思表达清楚，并且书写的格式要写成清晰易读的形式。它不用图形符号，因此书写方便、格式紧凑，容易修改，便于向计算机语言算法（即程序）过渡。

算法举例

1．枚举法

枚举法又称为穷举法，此算法将所有可能出现的情况一一进行测试，从中找出符合条件的所有结果。如计算“百钱买百鸡”问题，又如列出满足x*y=100的所有组合等。

例如计算一个古典数学问题——“百钱买百鸡”问题。一百个铜钱买了一百只鸡，公鸡每只5元，母鸡每只3元，小鸡3只1元，问公鸡、母鸡和小鸡各买几只？

假设公鸡x只，母鸡y只，小鸡z只。根据题意可列出以下方程组：

由于2个方程式中有3个未知数，属于无法直接求解的不定方程，故可采用“枚举法”进行试根。这里x,y,z为正整数，且z是3的倍数；由于鸡和钱的总数都是100，可以确定x,y,z的取值范围：

x的取值范围为1～20

y的取值范围为1～33

z的取值范围为3～99，步长为3

逐一测试各种可能的x（1到20）、y（1到33）、z（3到99）组合，并输出符合条件者。

对应的流程图如图所示：

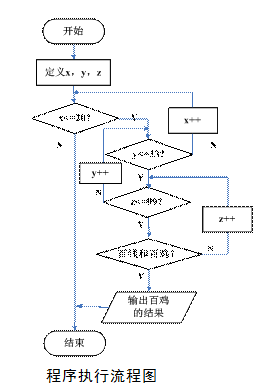
C语言程序代码如下：

#include<stdio.h>

main()

{

int x,y,z;

for(x=1;x<=20;x++)

    for(y=1;y<=33;y++)

        for(z=3;z<=99;z+=3)

        {

        /*是否满足百钱和百鸡的条件*/

if((5*x+3*y+z/3==100)&&(x+y+z==100))

     printf("cock=%d,hen=%d,chicken=%d\n",x,y,z);

        }

}

程序运行结果如下：

cock=4,hen=8,chicken=78

cock=8,hen=11,chicken=81

cock=12,hen=4,chicken=84

2．查找算法

查找也可称检索，是在数据集（大量的元素）中找到某个特定的元素的过程。查找算法(search algorithms)是在程序设计中最常用到的算法之一。例如，经常需要在大量商品信息中查找指定的商品、在学生名单中查找某个学生，等等。

有许多种不同的查找算法。根据数据集的特征不同，查找算法的效率和适用性也往往各不相同。顺序搜索、二分搜索、散列搜索等都是典型的查找算法。下面，就介绍这些典型搜索算法的思想和特点。

（1）顺序查找法

假定要从n个整数中查找x的值是否存在，最原始的办法是从头到尾逐个查找，这种查找的方法称为顺序查找。

设给定一个有10个元素的数组，其数据如图所示。list是数组名，其元素数据放在方格中。方格下面的方括号中的数字表示元素的下标，下标从0开始。list[0]表示数组list中的第一个元素，list[1]表示第二个元素，等等。

现在，希望找到数据75在list数组中的位置。二分查找过程如下：

①第一次搜索空间是整个数组，最左端的位置是0，最右端的位置是9，则其中间位置是4。比较75 与list[4]，75>list[4]，所以75应该落在整个数组的后半部分；

②这时开始第二次查找，搜索空间的最左端位的置是5，最右端的位置依然是9，计算得中间位置是7。比较75与list[7]，因为75<list[7]，继续折半搜索；

③第三次搜索空间的最左右端的位置分别是5和6，中间位置5，75>list[5] ，继续折半搜索；

④第四次搜索空间的最左右端的位置都是6，中间位置是6，且75=list[6]，停止查找，75的位置是6。

相应地，如果要查找数据91在list数组中的位置，查找过程如下：

①第一次的搜索空间，左端位置是0，右端位置是9，中间位置是4，比较91和 list[4]，91>list[4] ，继续折半搜索；

②第二次搜索空间的左右端位置分别是5和9，中间位置是7，91>list[7]。继续折半搜索；

③第三次搜索空间的左右端位置分别是8和9，中间位置是8，91<list[8]。继续折半搜索；

④第四次搜索空间的左端位置是8，右端位置是7，左端位置8>右端位置7，查找以失败结束，返回在list中没有发现元素与搜索项匹配的标志-1。

自然语言描述在list数组中进行二分查找算法如下：

①初始化左端位置left为0，右端位置right为list数组长度，同时设置找到标志found 为false；

②输入查找的数据key的值；

③判断left<=right和找到标志found为false是否同时成立，成立则转到第④步，否则转到第⑤步；

④计算中间位置mid ，如果list[mid]是要查找的数据key，则找到标志found赋值为true。如果list[mid]是大于要查找的数据key，则right=mid-1；如果list[mid]是小于要查找的数据key，则left=mid+1；转到③；

⑤判断found是否为true，是true说明找到了，则输出mid的值。否则说明没有找到，输出-1并结束搜索。

二分查找算法对应的流程图如图所示：

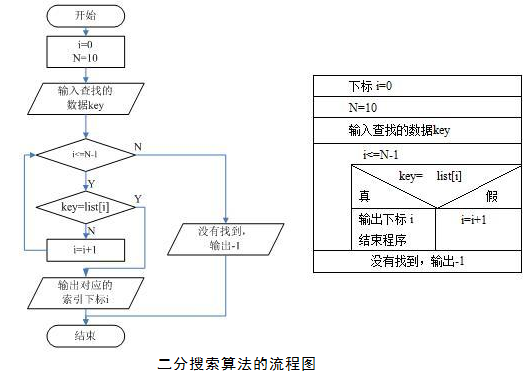
二分搜索算法有多种实现方式。如果采用循环方式，二分搜索算法的C语言代码如下：

#include<stdio.h>

main()

{ 

    int; list[10]= {2,11,18,29,32,51,75,82,96,125};

    int left=0, right=9 , mid=-1;   

    boolean found = false; 

         scanf("%d " ,&key)                /*输入查找key的值*/

    while(left<=right && found==false) 

    { 

        mid=(left+right)/2; 

        if(list[mid]==key) 

            found=true; 

        else  

            if(list[mid]> key ) 

                right=mid-1; 

            else 

                left=mid+1; 

    }     

    if(found==true)               /*是true说明找到了*/

        printf("%d",mid); 

    else 

        printf("-1"); 

}

3．排序算法

在处理数据过程中，经常需要对数据进行排序。甚至有人认为，在许多商业计算机系统中，可能有一半的时间都花费在了排序上面。这也说明了排序的重要性。许多专家对排序问题进行了大量研究，提出了许多有效的排序思想和算法。排序算法(sorting algorithms)是指将一组无序元素序列整理成有序序列的方法。根据排序算法的特点，可以分为互换类排序、插入类排序、选择类排序、合并类排序以及其他排序类算法等。下面，主要介绍冒泡排序、插入排序、选择排序等常用的排序算法。

（1）冒泡排序

冒泡排序(bubble sort)是一种简单的互换类排序算法，其基本思想是比较序列中的相邻数据项，如果存在逆序则进行互换，重复进行直到有序。

冒泡法排序法是每轮将相邻的两个数两两进行比较，若满足排序次序，则进行下一次比较，若不满足排序次序，则交换这两个数，直到最后。总的比较次数为n-1次，此时最后的元素为最大数或最小数，此为一轮排序。接着进行第二轮排序，方法同前，只是这次最后一个元素不再参与比较，比较次数为n-2次，依次类推。

冒泡排序基本思想参见图，黑体数字表示正在比较的两个数，最左列为最初的情况，最右列为完成后的情况。

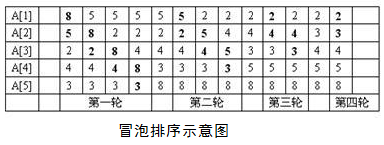
可以推知，如果有n个数，则要进行n-1轮比较(和交换)。在第1轮中要进行n-1次两两比较，在第j轮中要进行n-j次两两比较。

假设a数组存储从键盘输入的10个整数。对数组a的10个整数（为了描述方便，不使用a[0]元素，10个整数存入a[1]到a[10]中）的冒泡排序算法为：

第1轮遍历首先是a[1]与a[2]比较，如a[1]比a[2]大，则a[1]与a[2]互相交换位置；若a[1]不比a[2]大，则不交换。

第2次是a[2]与a[3]比较，如a[2]比a[3]大，则a[2]与a[3]互相交换位置；

第3次是a[3]与a[4]比较，如a[3]比a[4]大，则a[3]与a[4]互相交换位置；

……；

第9次是a[9]与a[10]比较，如a[9]比a[10]大，则a[9]与a[10]互相交换位置；第一次遍历结束后，使得数组中的最大数被调整到a[10]。

第二轮遍历和第一轮遍历类似，只不过因为第一轮遍历已经将最大值调整到了a[10]中，第二轮遍历只需要比较八次，第二轮遍历结束后，使得数组中的次大数被调整到a[9]。……；直到所有的数按从小到大的顺序排列。冒泡法排序（10个数按升序排列）的算法N-S图如图所示：

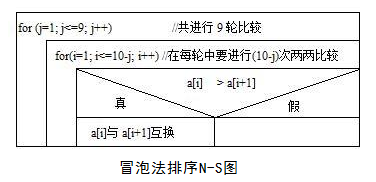
冒泡排序算法的伪代码如下所示：

FuncbubbleSort(array a) {

  for (j=1; j<=9; j++)                      //共进行9轮比较

    for(i=1; i<=10-j; i++)                //在每轮中要进行(10-j)次两两比较

       if (a[i]>a[i+1])                   //如果前面的数大于后面的数

       { a[i]与a[i+1]互换}              //交换两个数的位置，使小数上浮

}

（2）插入排序

插入排序(insertion sort)是一种将无序列表中的元素通过依次插入到已经排序好的列表中的算法。插入排序算法具有实现简单、对于少量数据排序效率高、适合在线排序等特点。

下面，通过一个示例来讲述插入排序的基本过程。对于一个有6个数据的无序数组：(12,6, 1, 15, 3, 19)，现在希望将该数组中的数据采用插入排序方法从小到大排列。排序过程如图所示。在每一个阶段，未被插入到排序列表中的数据使用阴影方框表示，列表中已排序的数据用白色方框表示，圆框表示数据的临时存储位置。在初始顺序中，第一个数据12表示已经排序，其他数据都是未排序数据。在排序过程的每个阶段中，第一个未排序数据被插入到已排序列表中的恰当位置。为了为这个插入值腾出空间，首先要把该插入值存储在临时圆框中，然后从已排序列表的末尾开始，逐个向前比较，移动数据项，直到找到该数据的合适位置为止。移动的数据使用箭头表示。

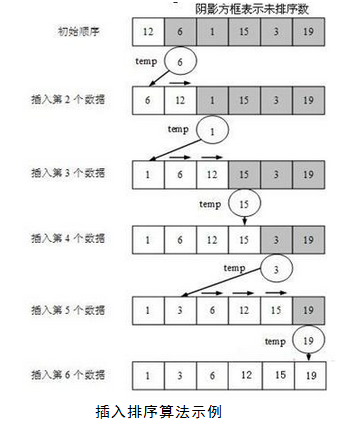
插入排序算法具体描述如下：

①从第一个元素开始，该元素可以认为已经被排序；

②取出下一个元素，在已经排序的元素序列中从后向前扫描；

③如果该元素（已排序）大于新元素，将该元素移到下一位置；

④重复步骤③，直到找到已排序的元素小于或者等于新元素的位置；

⑤将新元素插入到下一位置中；

⑥重复步骤2。

假设a数组存储从键盘输入的10个整数。对数组a的10个整数（为了描述方便，不使用a[0]元素，10个整数存入a[1]到a[10]中）的插入排序算法为：

第1轮插入是从第2个元素开始，将a[2]插入最初仅仅a[1]有序序列中。首先将a[2]值存储在变量temp中，将a[1]与temp比较。如a[1]比temp大则a[1]移到a[2]，最后temp放到空出的位置a[1]中；

2轮插入将a[3]插入到a[1]和a[2]有序序列中。首先将a[3]值存储变量temp中，将有序序最后元素a[2]与temp比较，如a[2]比temp大，则a[2] 移到a[3]，继续向前扫描直到已排序的元素小于或者等于temp，最后temp放到该元素下一位置中；

……；

第9轮插入将a[10]插入到a[1]，a[2],….到a[9]有序序列中。首先将a[10]值存储变量temp中，将有序序最后元素a[9]与temp比较，如a[9]比temp大，则a[9] 移到a[8]，继续向前扫描直到已排序的元素小于或者等于temp，最后temp放到该元素下一位置中。插入排序算法（10个数按升序排列）的算法N-S图如图所示：

插入排序算法的伪代码如下：

FuncinsertionSort(array a) 

{ 

    for (i = 2; i <= 10 ; i++)

    {

        temp = a[i]   //要插入的元素

        j = i - 1      //已经排序的元素序列最后元素下标

        while( j >= 1 and a[j] >temp)  //从后向前扫描，腾出空间

        { 

            a[j + 1] =a[j]  // a[j]前移

            j = j - 1 

        } 

        a[j + 1] = temp   //将新元素插入

    }

}

（3）选择排序

插入排序的一个主要问题是，即使大多数数据已经被正确排序在序列的前面，后面在插入数据时依然需要移动前面这些已排序的数据。选择排序算法可以避免大量已排序数据的移动现象。选择排序算法(selection sort)的主要思想是，扫描数据序列，找到最小的数据，将该数据交换到序列最前面的位置，然后对其余数据序列重复前面的步骤直到数据全部排序为止。

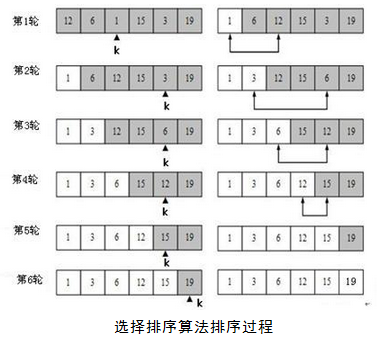
对于前面示例中的包含了6个数据的无序数组(12,6, 1, 15, 3, 19)，现在希望将该数组中的数据采用选择排序方法从小到大排列，排序过程如图所示。图中的阴影方框表示未排序数据。

在第1轮，首先扫描整个序列，找到最小元素1，然后将元素1与未排序序列中第1个位置的元素12互换。在第1阶段，未排序序列就是整个序列。

在第2轮，在未排序序列中找到最小元素3，然后将元素3与未排序序列中第1个位置的元素6互换。

继续进行，在第6轮时，由于只有一个数据19，因此排序结束。

设有10个数，存放在数组A中，选择法排序的算法如下：

首先引入一个指针变量k，用于记录每次找到的最小元素位置；

第1轮：k初始为1，即将指针指向第1个数（先假定第1个数最大）。将A[k]与A[2]比较，若A[k]<A[2]，则将k记录2，即将指针指向较大者。再将A[k]与A[3]~A[10]逐个比较，并在比较的过程中将k指向其中的较大数。完成比较后，k指向10个数中的最大者。如果k≠1，交换A[k]和A[1]；如果k=1，表示A[1]就是这10个数中的最大数，不需要进行换；

第2轮：将指针k初始为2（先假定第2个数最大），将A[k]与A[3]~A[10]逐个比较，并在比较的过程中将k指向其中的较大数。完成比较后，k指向余下9个数中的最大者。如果k≠2，交换A[k]和A[2]；如果k=2，表示A[2]就是这余下9个数中的最大数，不需要进行换；

继续进行第3轮、第4轮、……，直到第9轮。

选择法排序每轮最多进行一次交换，以n个数按降序排列为例，其流程图如图所示。其中，k≠i表示在第i轮比较的过程中，指针k曾经移动过，需要互换A[i]与A[k]，否则不进行任何操作。     

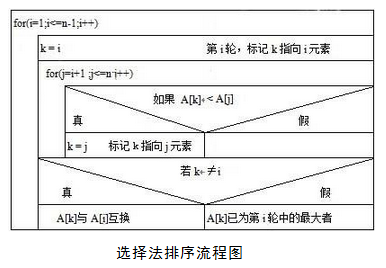
选择排序算法的伪代码如下：

FuncselectionSort(array A)  

{ 

    for (int i = 1; i <= A.length-1 ; i++){ 

        int k= i 

        for (int j = i + 1; j <= A.length;j++) { 

            if (A[j] < A[min])

                k= j             

        } 

        if ( k≠ i)

       { 

            A[k]与A[i]互换

        } 

    } 

}