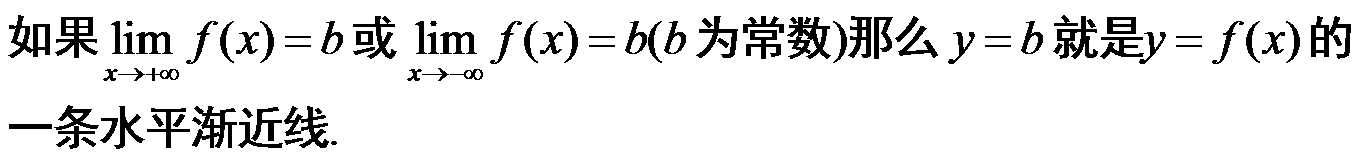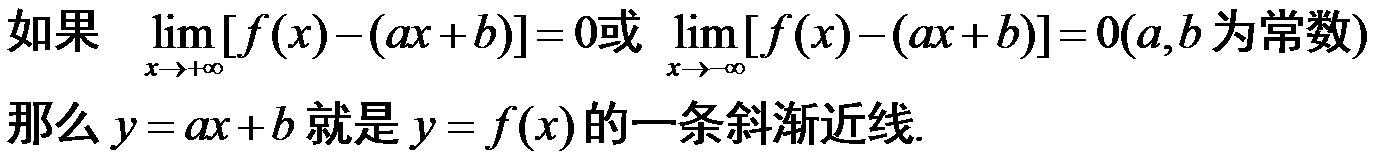第五节 函数图像的描绘
-
1 3.5(1)
-
2 3.5(2)
上一节
下一节
第五节 函数图像的描绘(1)
课程学习
重要知识点
一、函数的凹凸性
(1)定义:
1、凹函数:

2、凸函数:

如果上面定义中的不等式改为严格不等式,则相应的函数曲线称为
严格凸曲线和严格凹曲线,相应的函数为严格凸函数和严格凹函数。
(2)定理:

二、曲线的拐点及其求法
⑴ 定义:
连续曲线上凹凸的分界点称为曲线的拐点。
注意:拐点处的切线必在拐点处穿过曲线。
⑵ 拐点的求法:
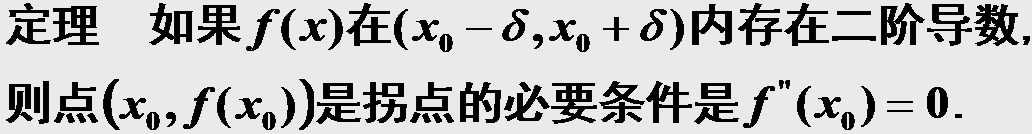

思考题

知识拓展
3