2.3 The Close Packed Solid

¡We have already said that the solid differs from the other states of matter in that a long range ordering of atoms or molecules has appeared.

¡All of the atoms should be required to be arranged in a symmetrical pattern in three dimensions.--building blocks, propagation models

¡In general, there are two kinds of solids, homogeneous and heterogeneous.

¡Homogeneous solid is composed from atoms that are all the same.

¡Heterogeneous solid is composed from atoms not the same.

¡If the atoms are all of one kind, i.e.-one of the elements, the problem is straight forward.

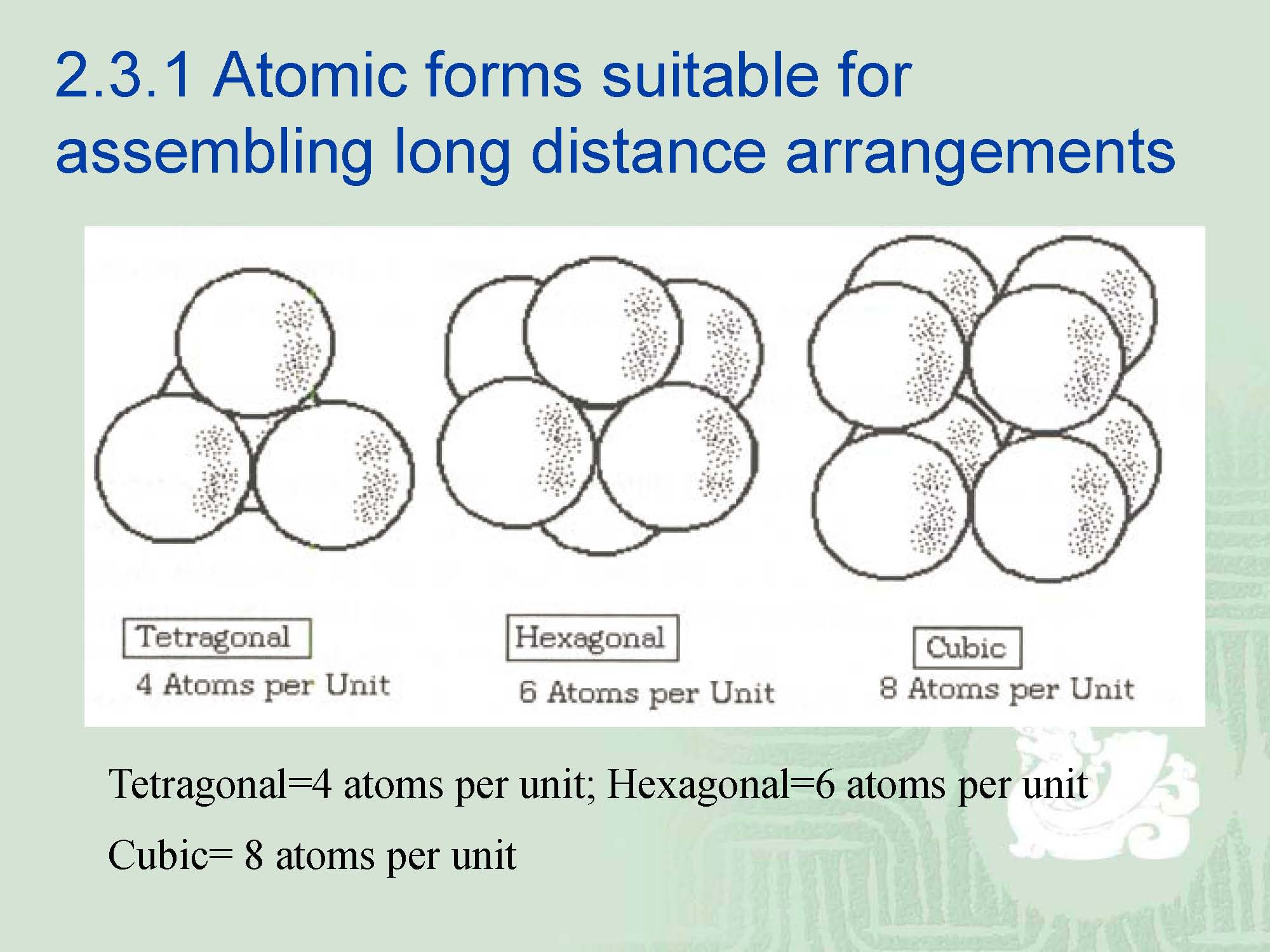
¡Sets of 8 atoms, each set arranged as a cube, will generate a cubic structure.

¡Two sets of 3 atoms, each set of three arranged in a triangle, will propagate a hexagonal pattern with three dimensional symmetry.

¡Elemental solids having a tetragonal structure are very few and it is easy to ascertain that most of the elements from structures that are either cubic or hexagonal,but rarely tetragonal.

¡The reason for this is that tetragonal units are more conductive for the case where not all of the atoms are the same, i.e.--heterogeneous case.e.g.  -PO4;   -CO3

¡There is also another important factor. Thatis, in building a solid structure are based on the largest atom present, as well as how it stacks together in space filling-form.

¡For most inorganic compounds, this is the oxygen atom, e.g.- oxides, silicates, phosphates, sulfates, borates, tungstates, vanadates, etc.

¡The few exceptions involve chalcogenides (氧、硫化物), halides（卤化物）, hydrides, etc.

¡Thus 4 atoms will form a 3-dimensional tetrahedron which is valid propagation unit.-pyramid

¡This means that we can take tetrahedrons and fit them together 3-dimensionally to form a symmetrical structure which extendsto infinity.

¡However, if one more atom is added to the pyramid, we then have an octahedron which is space-filling with translational properties. This results in a hexagonal structure.

¡Going further, combinations of seven atoms are asymmetrical, but eight atoms form a cube which can be propagated to infinity to form a cubic structure.

2.3.4 Propagation unitsusually found in solids

¡Tetrahedron-4

¡Octahedron-6

¡Hexagon-6or 8

¡Cube-8

¡We conclude that structures of solids are based, in general, upon these four basic propagation units, which can be stacked in a symmetrical and space-filling form to near infinity.

¡The symmetry will be that of the largest atoms in the structure, usually oxygen in inorganic solids.

¡In many cases they are smaller and will fitinto the interstice of the propagation unit, illustrated by the PO4-tetrahedron mentioned above. 

¡In this case, the P5+ atom is small enough to fit into the center(interstice) of the tetrahedron formed by the four oxygen atoms.

2.3.5 Known calcium silicates

¡For example, a large number of calcium silicates are known, including:

¡Ca2SiO3,Ca3Si2O7, CaSi2O5, Ca2SiO4, Ca4(Si4O17)(OH)2,  Ca4SiO7(OH)2, Ca9Si6O21(OH),  CaSiO3 ---58 known compounds

In order to differentiate among such complicated systems, i.e.-oxygenated compounds of calcium and silicon, we resort to what that is called a “phase-diagram”.