矩阵与空间变换
依据能否便捷的被数学函数公式精确描述,空间变换可以分为两大类:简单变换和复杂变换。位移、反射、旋转、斜切等变换都可以通过简单的函数来描述属于简单变换;在Photoshop中对一幅图像应用涂抹工具,是复杂变换,需要根据具体情况具体处理。
简单空间变换是计算机图形学的重要研究内容,其运算是依靠矩阵来描述的。使用脚本控制动画形变,主要是进行简单空间变换。AS3中的Matrix类提供了处理简单空间变换的能力,其本质就是矩阵操作。
假设舞台平面内存在一个点S(x,y),可以将其看成一个一行两列的矩阵A[x,y],如果企图使之水平方向放大两倍,则目标点T的坐标为(2x,y),依然可以看成一个矩阵C
[2x,y]。假设有一个矩阵B,满足A×B=C,那么矩阵B就是一个变换矩阵,其功能为令对象水平拉伸2倍。数学已经证明B是存在的,而且可以断言,矩阵B是一个2×2的矩阵。假设矩阵B内的元素为[(a,b),(c,d)],如图8-29所示:
根据矩阵乘法,可以写出以下方程组。
为使这个方程组成立,只需要令a=2,b=0,c=0,d=1即可。
轴对称变换:由一个图形变为另一个图形,并使这两个图形关于某一条直线成轴对称,这样的图形改变叫做图形的轴对称变换,也叫做反射变换,简称反射(reflection)。轴对称变换不改变原图形的形状和大小。
平移变换:由一个图形改变为另一个图形,在改变过程中,原图形上所有的点都向同一个方向运动,且运动相等的距离,这样的图形改变叫做图形的平移变换,简称平移。
旋转变换:由一个图形改变为另一个图形,在改变过程中,原图形上所有的点都围绕一个固定的点按同一个方向,旋转同一个角度,这样的图形改变叫做图形的旋转变换,简称旋转。这个点称为旋转中心,转动的角称为旋转角。
相似变换:由一个图形到另一个图形,在改变的过程中保持形状不变(大小方向和位置可变),这样的图形改变叫做图形的相似变换(similarty
transformation)。图形的相似变换不改变图形中每一个角的大小。
仿射变换是空间直角坐标变换的一种,它是一种二维坐标到二维坐标之间的线性变换,保持二维图形的“平直线”和“平行性”,其可以通过一系列的原子变换的复合来实现,包括平移(Translation)、缩放(Scale)、翻转(Flip)、旋转(Rotation)和剪切(Shear)。
此类变换可以用一个3×3的矩阵来表示,其最后一行为(0, 0, 1)。该变换矩阵将原坐标(x, y)变换为新坐标(x',
y'),这里原坐标和新坐标皆视为最末一行为(1)的三维列向量,原列向量左乘变换矩阵得到新的列向量:
[x'] [m00 m01 m02] [x] [m00*x+m01*y+m02]
[y'] = [m10 m11 m12] [y] = [m10*x+m11*y+m12]
[1 ] [ 0 0 1 ] [1] [ 1 ]
用代数式表示如下:
x’ = m00*x+m01*y+m02;
y’ = m10*x+m11*y+m12;
如果将它写成按旋转、缩放、平移三个分量的复合形式,则其代数式如下:
X= (x-x0)cosθ+(y-y0)sinθ+x0
Y=-(x-x0)sinθ+(y-y0)cosθ+y0
其示意图如下:
几种典型的仿射变换:
1.public static AffineTransform getTranslateInstance(double tx, double
ty)
平移变换,将每一点移动到(x+tx, y+ty),变换矩阵为:
[ 1 0 tx ]
[ 0 1 ty ]
[ 0 0 1 ]
(译注:平移变换是一种“刚体变换”,rigid-body
transformation,中学学过的物理,都知道啥叫“刚体”吧,就是不会产生形变的理想物体,平移当然不会改变二维图形的形状。同理,下面的“旋转变换”也是刚体变换,而“缩放”、“错切”都是会改变图形形状的。)
2.public static AffineTransform getScaleInstance(double sx, double sy)
缩放变换,将每一点的横坐标放大(缩小)至sx倍,纵坐标放大(缩小)至sy倍,变换矩阵为:
[ sx 0 0 ]
[ 0 sy 0 ]
[ 0 0 1 ]
3.public static AffineTransform getShearInstance(double shx, double shy)
剪切变换,变换矩阵为:
[ 1 shx 0 ]
[ shy 1 0 ]
[ 0 0 1 ]
相当于一个横向剪切与一个纵向剪切的复合
[ 1 0 0 ][ 1 shx 0 ]
[ shy 1 0 ][ 0 1 0 ]
[ 0 0 1 ][ 0 0 1 ]
(译注:“剪切变换”又称“错切变换”,指的是类似于四边形不稳定性那种性质,街边小商店那种铁拉门都见过吧?想象一下上面铁条构成的菱形拉动的过程,那就是“错切”的过程。)
4.public static AffineTransform getRotateInstance(double theta)
旋转变换,目标图形围绕原点顺时针旋转theta弧度,变换矩阵为:
[ cos(theta) -sin(theta) 0 ]
[ sin(theta) cos(theta) 0 ]
[ 0 0 1 ]
5.public static AffineTransform getRotateInstance(double theta, double x,
double y)
旋转变换,目标图形以(x, y)为轴心顺时针旋转theta弧度,变换矩阵为:
[ cos(theta) -sin(theta) x-x*cos+y*sin]
[ sin(theta) cos(theta) y-x*sin-y*cos ]
[ 0 0 1 ]
相当于两次平移变换与一次原点旋转变换的复合:
[1 0 -x][cos(theta) -sin(theta) 0][1 0 x]
[0 1 -y][sin(theta) cos(theta) 0][0 1 y]
[0 0 1 ][ 0 0 1
][0 0 1]
三、仿射变换四参数求解
A、C#自定义函数实现求解:
1、求解旋转参数Rotaion:
///
///获取旋转角度
///
///源点1
///目标点1
///源点2
///目标点2
///返回旋转角度
private double GetRotation(CoordPoint fromPoint1, CoordPoint toPoint1,CoordPoint
fromPoint2,CoordPoint
toPoint2)
{
double a = (toPoint2.Y - toPoint1.Y) * (fromPoint2.X - fromPoint1.X) -
(toPoint2.X - toPoint1.X) * (fromPoint2.Y -
fromPoint1.Y);
double b = (toPoint2.X - toPoint1.X) * (fromPoint2.X - fromPoint1.X) +
(toPoint2.Y - toPoint1.Y) * (fromPoint2.Y -
fromPoint1.Y);
if (Math.Abs(b) >
0)
return Math.Tan(a /
b);
else
return
Math.Tan(0);
}
2、求解缩放比例参数(Scale):
///
///获取缩放比例因子
///
///源点1
///目标点1
///源点2
///目标点2
///旋转角度
///返回旋转因子
private double GetScale(CoordPoint fromPoint1, CoordPoint toPoint1, CoordPoint
fromPoint2, CoordPoint toPoint2, double
rotation)
{
double a = toPoint2.X -
toPoint1.X;
double b = (fromPoint2.X - fromPoint1.X) * Math.Cos(rotation) - (fromPoint2.Y -
fromPoint1.Y)*Math.Sin(rotation);
if (Math.Abs(b) >
0)
return a /
b;
else
return
0;
}
3、求解X方向偏移距离参数(XTranslate):
///
///得到X方向偏移量
///
///源点1
///目标点1
///旋转角度
///缩放因子
///返回X方向偏移量
private double GetXTranslation(CoordPoint fromPoint1,CoordPoint toPoint1,double
rotation,double
scale)
{
return (toPoint1.X - scale * (fromPoint1.X * Math.Cos(rotation) - fromPoint1.Y *
Math.Sin(rotation)));
}
4、求解Y方向偏移距离参数(YTranslate):
///
///得到Y方向偏移量
///
///源点1
///目标点1
///旋转角度
///缩放因子
///返回Y方向偏移量
private
double GetYTranslation(CoordPoint fromPoint1, CoordPoint toPoint1, double
rotation, double scale)
{
return (toPoint1.Y - scale * (fromPoint1.X * Math.Sin(rotation) + fromPoint1.Y *
Math.Cos(rotation)));
}
B、C#+AE求解:
///
///从控制点定义仿射变换程式
///
///源控制点
///目标控制点
///返回变换定义
private ITransformation GetAffineTransformation(IPoint[] pFromPoints, IPoint[]
pToPoints)
{
//实例化仿射变换对象
IAffineTransformation2D3GEN tAffineTransformation = new
AffineTransformation2DClass();
//从源控制点定义参数
tAffineTransformation.DefineFromControlPoints(ref pFromPoints, ref
pToPoints);
//查询引用接口
ITransformation tTransformation = tAffineTransformation as ITransformation;
return tTransformation;
}
四、空间对象转换
求出参数后,再利用公式对相应坐标点进行转换是一件相对简单的事件了。
示例代码:
///
///从控制点定义仿射变换程式
///
///源控制点
///目标控制点
///返回变换定义
private
ITransformation GetAffineTransformation(IPoint[] pFromPoints, IPoint[]
pToPoints)
{
//实例化仿射变换对象
IAffineTransformation2D3GEN tAffineTransformation = new
AffineTransformation2DClass();
//从源控制点定义参数
tAffineTransformation.DefineFromControlPoints(ref pFromPoints, ref
pToPoints);
//查询引用接口
ITransformation tTransformation = tAffineTransformation as ITransformation;
return tTransformation;
}
什么是仿射变换:
一个任意的仿射变换都能表示为 乘以一个矩阵 (线性变换) 接着再 加上一个向量 (平移)
所以,能够用仿射变换来表示:
旋转 (线性变换)
平移 (向量加)
缩放操作 (线性变换)
简单的说,仿射变换代表的是两幅图之间的
关系 (位置关系).
3. 通常使用2×3的矩阵来进行仿射变换。比如用 A,B矩阵 对 X矩阵 进行仿射变换就是:
T=A·X+B;
矩阵中存储的是位置坐标。
以下面两幅图为例:

图片1与图片2中的3个点存在一一对应的关系,通过这样两组三点求出仿射变换矩阵,就能把仿射变换应用到图像中所有的点,求出仿射变换后的图像。
用到的函数:
getRotationMatrix2D
来获得一个 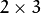 旋转矩阵
旋转矩阵
warpAffine
来实现一些简单的仿射变换.
程序代码及注释:
// 042 仿射变换.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "opencv2/highgui/highgui.hpp"
#include
"opencv2/imgproc/imgproc.hpp"
#include <iostream>
#include
<stdio.h>
using namespace cv;
using namespace std;
/// 全局变量
char* source_window = "Source image";
char* warp_window =
"Warp";
char* warp_rotate_window = "Warp + Rotate";
int main( int argc, char** argv )
{
//
//两个需要用来定义仿射变换的二维点数组,源图像和目标图像上分别一一映射的三个点
Point2f
srcTri[3];
Point2f dstTri[3];
//仿射变换矩阵
Mat rot_mat( 2, 3, CV_32FC1
);
Mat warp_mat( 2, 3, CV_32FC1 );
Mat src, warp_dst, warp_rotate_dst;
src = imread( "Lena.jpg" );
/// 设置目标图像的大小和类型与源图像一致
warp_dst = Mat::zeros(
src.rows, src.cols, src.type() );
/// 设置源图像和目标图像上的三组点以计算仿射变换
srcTri[0] = Point2f(
0,0 );
srcTri[1] = Point2f( src.cols - 1, 0 );
srcTri[2] = Point2f( 0, src.rows - 1 );
dstTri[0] = Point2f( src.cols*0.0, src.rows*0.33
);
dstTri[1] = Point2f( src.cols*0.85, src.rows*0.25
);
dstTri[2] = Point2f( src.cols*0.15, src.rows*0.7 );
/// 求得仿射变换,即仿射变换的2*3数组
warp_mat =
getAffineTransform( srcTri, dstTri );
/// 对源图像应用上面求得的仿射变换
warpAffine( src, warp_dst,
warp_mat, warp_dst.size() );
// 对上面得到的扭曲进行旋转操作
/// 计算绕图像中点顺时针旋转50度缩放因子为0.6的旋转矩阵
Point center =
Point( warp_dst.cols/2, warp_dst.rows/2 );
double angle =
-50.0; //顺时针旋转
//double
scale = 0.6;
double scale = 1;
/// 通过上面的旋转细节信息求得旋转矩阵,即仿射变换的2*3矩阵
rot_mat =
getRotationMatrix2D( center, angle, scale );
/// 旋转已扭曲图像,即仿射变换
warpAffine( warp_dst,
warp_rotate_dst, rot_mat, warp_dst.size() );
/// 显示结果
namedWindow( source_window,
CV_WINDOW_AUTOSIZE );
imshow( source_window, src );
namedWindow( warp_window, CV_WINDOW_AUTOSIZE );
imshow( warp_window, warp_dst );
namedWindow( warp_rotate_window, CV_WINDOW_AUTOSIZE
);
imshow( warp_rotate_window, warp_rotate_dst );
waitKey(0);
return 0;
}
运行结果:

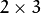 旋转矩阵
旋转矩阵

