高等数学

陈洪宇

目录

  • 1 第一章 函数、极限、连续
    • 1.1 函数及其性质
    • 1.2 初等函数
    • 1.3 数列的极限
    • 1.4 函数的极限
    • 1.5 无穷小与无穷大
    • 1.6 极限的四则运算法则
    • 1.7 两个重要极限
    • 1.8 无穷小的比较
    • 1.9 函数的连续性
  • 2 第二章 导数与微分
    • 2.1 导数的概念
    • 2.2 导数公式与四则运算求导法则
    • 2.3 复合函数的导数
    • 2.4 隐函数的导数
    • 2.5 高阶导数
    • 2.6 函数的微分
  • 3 第三章 导数的应用
    • 3.1 微分中值定理
    • 3.2 洛必达法则
    • 3.3 函数的单调性
    • 3.4 函数的极值
    • 3.5 函数的最值
    • 3.6 曲线的凹凸性
    • 3.7 函数图像的描绘
  • 4 第四章 不定积分
    • 4.1 不定积分的概念与性质
    • 4.2 换元积分法
    • 4.3 分部积分法
  • 5 第五章 定积分及其应用
    • 5.1 定积分的概念与性质
    • 5.2 微积分基本公式
    • 5.3 定积分的换元法
    • 5.4 定积分的分部积分法
    • 5.5 定积分应用之平面图形的面积
    • 5.6 定积分应用之旋转体的体积
导数的概念
  • 1 学习目标
  • 2 视频
  • 3 课件、教案
  • 4 本节测验

1.理解导数的概念.关于导数的概念，要理解其本质，掌握导数定义式的两种表达形式，定义式中自变量的增量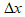用其他字符表达时，要能准确识别，并学会用换元的思想变形导数的定义式.

2.理解导数的几何意义，学会求曲线的切线和法线方程.

3.理解函数的可导性与连续性的关系.特别注意判断分段函数的可导性与连续性时要看清函数的分段方式，是否需要分左右导数和左右连续考虑.