数与代数

数与代数是义务教育阶段学生数学学习的重要领域，在小学阶段包括“数与运算"和“数量关系"两个主题。学段之间的内容相互关联，由浅入深，层层递进，螺旋上升，构成相对系统的知识结构。

“数与运算”包括整数、小数和分数的认识及其四则运算。数是对数量的抽象，数的运算重点在于理解算理、掌握算法，数与运算之 间有密切的关联。学生经历由数量到数的形成过程，理解和掌握数的概念；经历算理和算法的探索过程，理解算理，掌握算法。初步体会数是对数量的抽象，感悟数的概念本质上的一致性，形成数感和符号意识；感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识。

“数量关系”主要是用符号（包括数）或含有符号的式子表达数量之间的关系或规律。学生经历在具体情境中运用数量关系解决问题 的过程，感悟加法模型和乘法模型的意义，提高发现和提出问题、分析和解决问题的能力，形成模型意识和初步的应用意识。

第一学段（1〜2年级）

【内容要求】

1. 数与运算

（1）在实际情境中感悟并理解万以内数的意义，理解数位的含义，知道用算盘可以表示多位数（例1）。

（2）了解符号V,=, ＞的含义，会比较万以内数的大小；通过数的大小比较，感悟相等和不等关系（例2）。

（3）在具体情境中，了解四则运算的意义，感悟运算之间的关系（例3）。

（4）探索加法和减法的算理与算法，会整数加减法。

（5）探索乘法和除法的算理与算法，会简单的整数乘除法。

（6）在解决生活情境问题的过程中，体会数和运算的意义，形成初步的符号意识、数感、运算能力和推理意识。

【学业要求】

1. 数与运算

能用数表示物体的个数或事物的顺序，能认、读、写万以内的数；能说出不同数位上的数表示的数值；能用符号表示数的大小关系 （例6）,形成初步的数感和符号意识。

能描述四则运算的含义，知道减法是加法的逆运算、乘法是加法的简便运算、除法是乘法的逆运算；能熟练口算20以内数的加减法和表内乘除法，能口算简单的百以内数的加减法；能计算两位数和三 位数的加减法。形成初步的运算能力。

【教学提示】

第一学段是学生进入小学学习的开始，要充分考虑学生在幼儿园阶段形成的活动经验和生活经验，遵循本阶段学生的思维特点和认知 规律，为学生提供生动有趣的活动，更好地完成从幼儿园阶段到小学阶段的学习过渡。

数与运算的教学。数的认识与数的运算具有密切的联系，既要注重各自的特征，也要关注二者的联系。数的认识是数的运算的基础， 通过数的运算有助于学生更好地认识数。

数的认识教学应提供学生熟悉的情境，使学生感受具体情境中的数量，可以用对应的方法，借助小方块、圆片和小棒等表示相等的数量，然后过渡到用数字表达，使学生体会可以用一个数字符号表示同样的数量；知道不同数位上的数字表示不同的值。教学中应注意，10 以内数的教学重点是使学生体验1〜9从数量到数的抽象过程，通过9 再加1就是十，体会十的表达与1〜9的不同是在新的位置上写1,这个位置叫十位，十位上的1表示1个十，1个十用数字符号10表达。 同理认识百以内数、万以内数。通过数量多少的比较，理解数的大小 关系（例7）。在这样的教学活动中，帮助学生形成初步的符号意识和数感。

数的运算教学应让学生感知数的加减运算要在相同数位上进行, 体会简单的推理过程。引导学生通过具体操作活动，利用对应的方法理解加法的意义，感悟减法是加法的逆运算；在具体情境中，启发学生理解乘法是加法的简便运算，感悟除法是乘法的逆运算。在教学活动中，始终关注学生运算能力和推理意识的形成与发展。

第二学段（3〜4年级）

【内容要求】

1. 数量关系

（1）在实际情境中，运用数和数的运算解决问题；在解决实际问 题的过程中，能结合具体情境，选择合适的单位进行简单估算，体会 估算在生活中的作用（例11）。

（2）能借助计算器进行计算，解决简单的实际问题，探索简单的规律（例12）。

（3）在具体情境中，认识常见数量关系：总量=分量+分量（例13）、总价=单价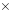数量、路程=速度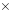时间；能利用这些关系解决 简单的实际问题。

（4）能在具体情境中了解等量的等量相等。

（5）能解决生活中的简单问题，并能对结果的实际意义作出解释，经历探索简单规律的过程（例14）,形成初步的模型意识和应用意识。

【学业要求】

2.数量关系

能在简单的实际情境中，运用四则混合运算解决问题，能选择合适的单位通过估算解决实际问题，形成初步的应用意识。

能在真实情境中，发现常见数量关系，感悟利用常见数量关系解决问题；能借助计算器进行计算，并解释计算结果的实际意义；形成初步的模型意识、几何直观和应用意识。

能在真实情境中，合理利用等量的等量相等进行推理，形成初步的推理意识（例15）。

【教学提示】

数量关系的教学。在具体情境中，利用加法或乘法表示数量之间 的关系，建立加法模型和乘法模型，知道模型中数量的意义。估算的 重点是解决实际问题。

常见数量关系的教学要在了解四则运算含义的基础上，引导学生理解现实问题中的加法模型是表示总量等于各分量之和，乘法模型可大体分为与个数有关（总价=单价X数量）和与物理量有关（路程= 速度X时间）的两种形式，感悟模型中量纲的意义。应设计合适的问 题情境，引导学生分析和表达情境中的数量关系，启发学生会用数学 的语言表达现实世界，形成初步的模型意识，提升问题解决能力。利 用现实背景，引导学生理解等量的等量相等这一基本事实，形成初步 的推理意识（例15）。

估算教学要引导学生在具体的问题情境中选择合适的单位进行估算，体会估算在解决实际问题中的作用，了解估算的实际意义。

第三学段（5〜6年级）

【内容要求】

2.数量关系

（1）根据具体情境理解等式的基本性质（例17）。

（2）在解决实际问题的过程中，会选择合适的方法进行估算（例18）。

（3）在具体情境中，探索用字母表示事物的关系、性质和规律的方法，感悟用字母表示的一般性（例19）。

（4）在实际情境中理解比和比例以及按比例分配的含义，能解决简单的问题。

（5）通过具体情境，认识成正比的量（如,y/x=5）（例20）；能探索规律或变化趋势（如y=5z）（例21）。

（6）能运用常见的数量关系解决实际问题，能合理解释结果的实际意义，逐步形成模型意识和几何直观，提高解决问题的能力

【学业要求】

1. 数量关系

能在具体问题中感受等式的基本性质（例17）。

能在解决实际问题中运用恰当的方法进行估算，并能描述估算的过程。

能在具体情境中，用字母或含有字母的式子表示数量之间的关系、性质和规律，感悟用字母表示具有一般性。

能在具体情境中判断两个量的比，会计算比值，理解比值相同的量，能解决按比例分配的简单问题。

能在具体情境中描述成正比的量,能找出生活中成X正比的量的实例；能根据给出的成正比关系的数据在方格纸上画图， 了解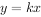的形式，能根据其中一个量的值计算另一个量的值。

能解决较复杂的真实问题，形成几何直观和初步的应用意识，提高解决问题的能力。

【教学提示】

数量关系的教学。理解用字母表示的一般性，形成初步的代数思维。

用字母表示的教学要设计合理的实际情境，引导学生会用字母或 含有字母的式子表达实际情境中的数量关系、性质和规律。例如：用字母表达常见数量关系及其变形，“路程=速度X时间”表示为s = vXt；还可以表达图形 的周长和面积计算公式等，感受字母表达的一般性。运用数和字母表 达数量关系，通过运算或推理解决问题（例23）,形成与发展学生的符号意识、推理意识和初步的应用意识。

估算教学要借助真实情境，引导学生在选择合适单位估算的基础上，感悟选择合适的方法估算的重要性，提高解决问题的能力，发展 初步的应用意识。

比和比例教学要合理利用实际生活中的情境，引导学生发现并用字母表达两个数量之间的倍数关系。例如，通过同样照片的放大与缩小、食品中原料的成分比等，理解比例的意义，能解决简单的按比例 分配的问题。

成正比的量教学要在具体情境中呈现两个成正比的量的变化规律，感悟这两个表达式的共性与差异；引导学生尝试在方格纸上画出给定的成正比的量的数据，建立几何直 观，为初中学习函数积累经验。