
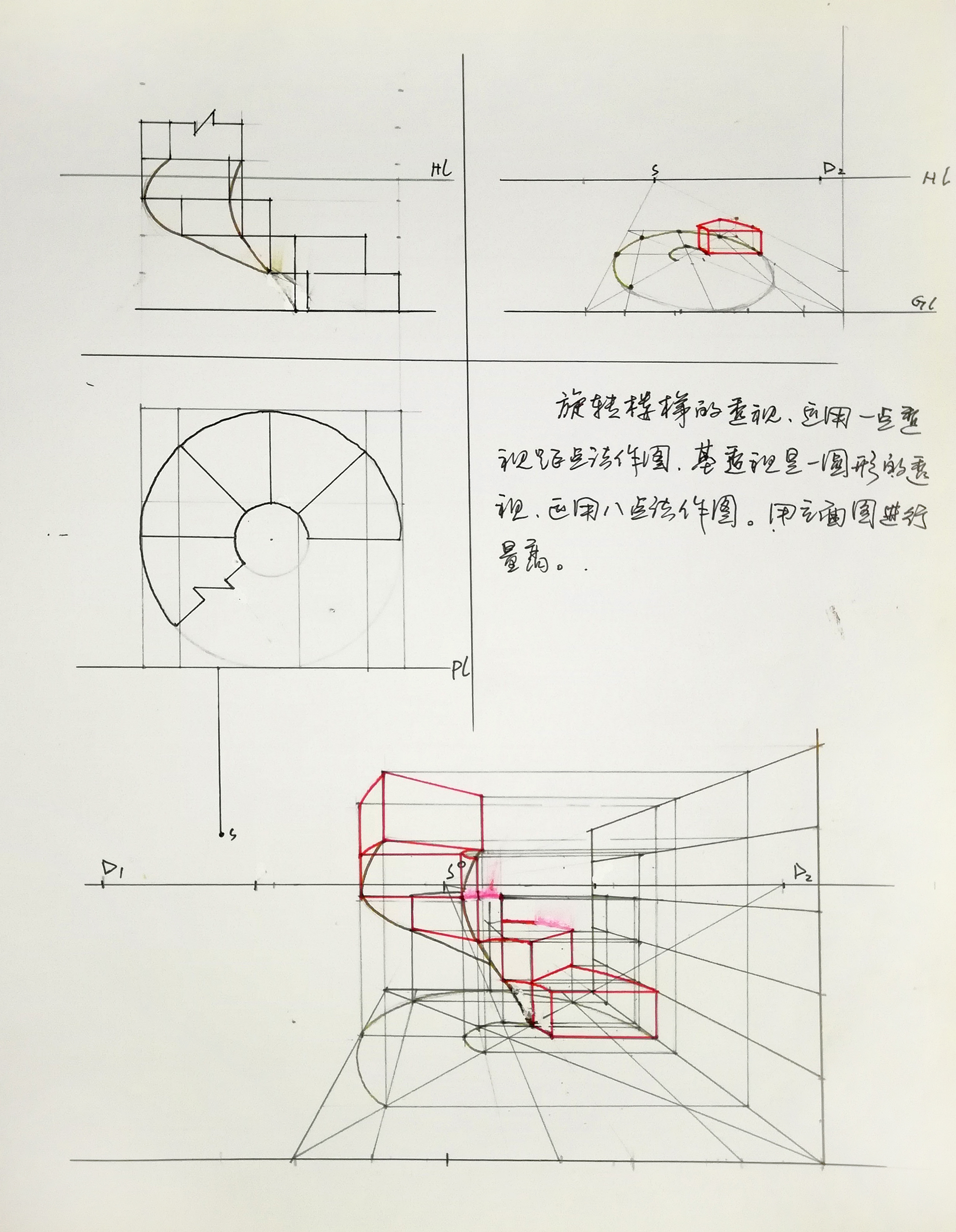
2.8 圆的透视与建筑细部透视
2.8.1曲线及圆形透视的原理和作图方法
学习重点:正确认识曲线及圆形透视的基本规律和掌握其透视的作图方法。
学习难点:圆形透视除本身的形产生近大远小的透视变化外,由于圆面所处的位置左右高低不同,它的透视形也会产生各种不同的变化。
曲线及圆形透视的概念
由曲线和曲面构成的景物很多.是绘画创作经常描绘的对象。因此,除了方形景物的透视画法和透视规律以外,还应该了解曲线和曲面的透视画法和规律。
曲线在一个平面内的叫做平面曲线。曲线在空间中的叫做立体曲线或空间曲线,如螺旋线。平面曲线和立体曲线又可分为规则曲线和不规则的曲线。规则曲线是有规律的曲线,一般的几何曲线如圆线、椭圆线、抛物线、渐开线等。不规则曲线是指无规律的任意曲线。由曲面构成的物体一般可以分解为一些平面曲线,因此本章着重介绍规则曲线,特别是圆线的透视画法、规律及应用。同时简要介绍不规则曲线的透视画法。












曲线及圆形透视的作图方法

(1)圆的透视画法
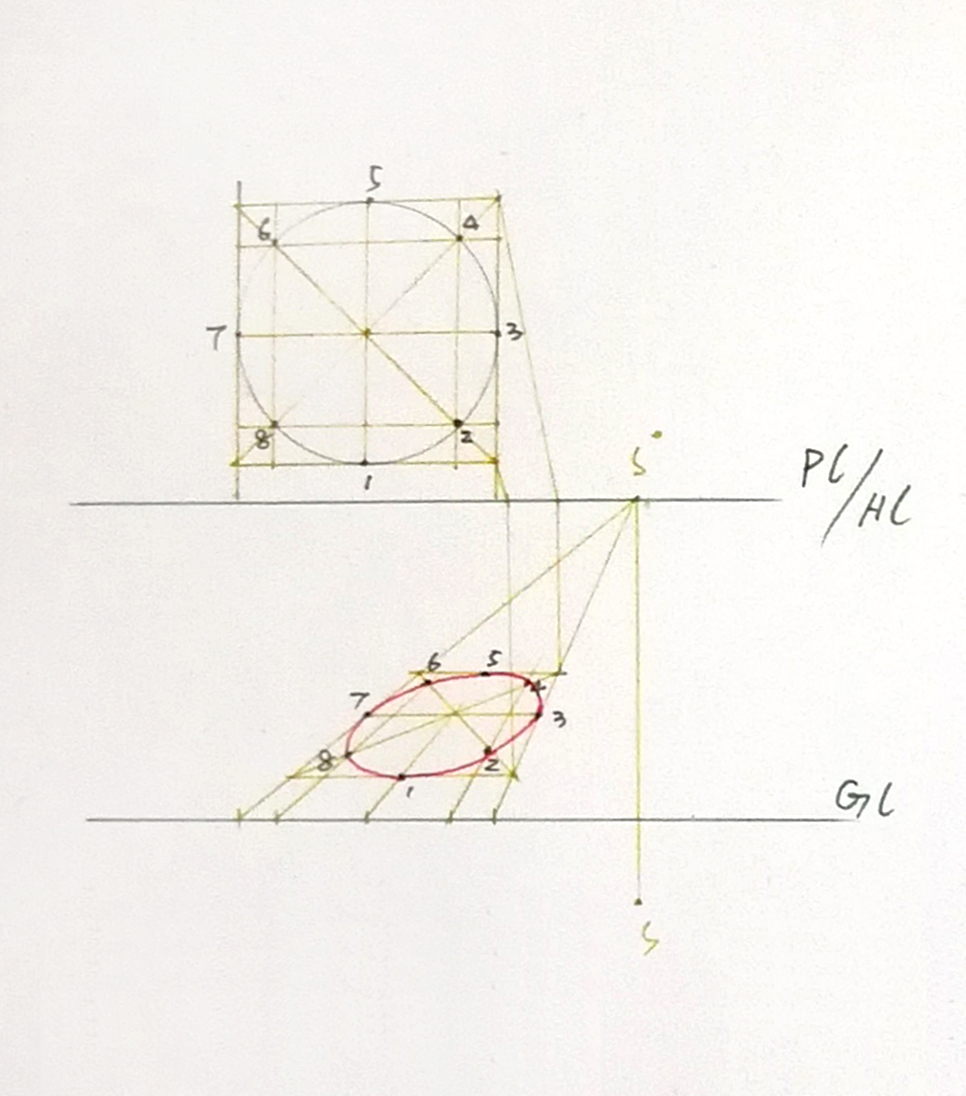
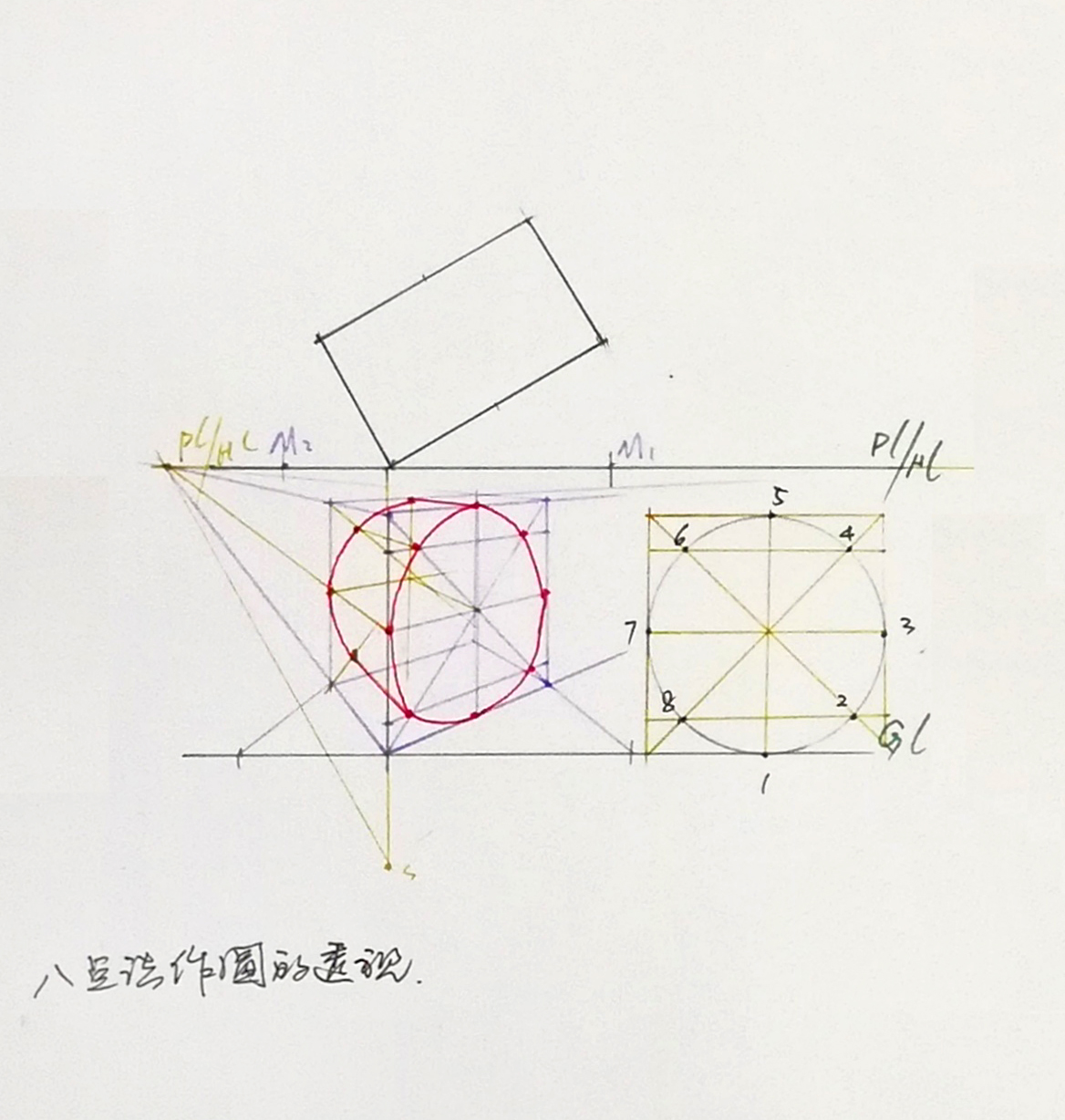
八点画法
画平面曲线透视的基本方法是把平面曲线置于矩形之内,先画出矩形及一些辅助线的透视,求出平面曲线与矩形和这些辅助线的交点,然后用曲线连接而成。即圆的透视的基本画法:首先作出圆的外切正方形,以及正方形的中心线和对角线,这样与圆周有8个交点。作透视图时先画出正方形及对角线和中心线的透视,求出所需8个交点,然后用曲线连接各点画出圆的透视。用这种方法可不画出平面图,从而节省作图时间。

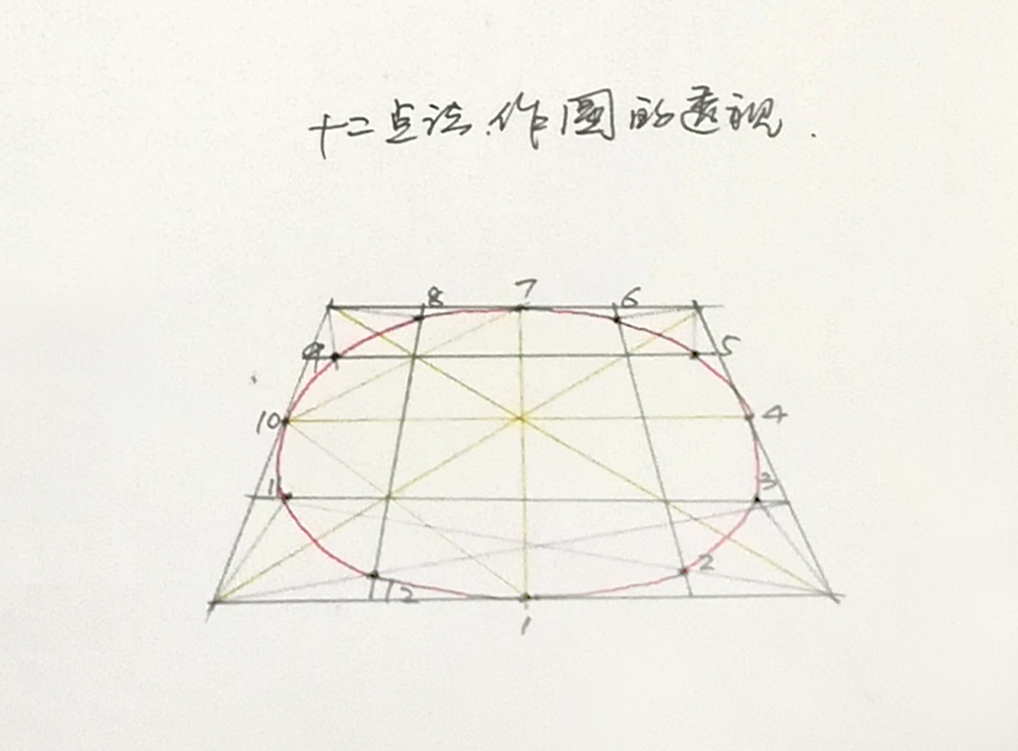
十二点求圆法
在需要画出较大的透视圆形时,为了画得准确些,可以运用12点求圆法。

(2)圆形透视的基本规律
A.平行于画面的圆的透视仍为正圆形,只有近大远小的透视变化。
平行于画面的等大的圆的透视形,无论在什么位置,都是正圆,只是由于远近不同而有近大远小的透视变化,图中远近三组各有3个圆至画面的距离相等,因此同远近的圆均为等大的正圆。

b.垂直于画面的圆的透视一般为椭圆。从长轴分前后样大,但从直径分,则远的半圆较小,近的半圆较大,见本章各图。要注意的是,透视圆的最宽长轴不是直径,画透视圆形时,弧线要均匀自然,特别是两端要弯曲自然。
b.垂直于画面的圆的透视形虽然基本为椭圆,但由于圆面所处的位置左右高低不同它的透视形也就产生各种变化。
c.主垂线或视平线通过圆心的圆面为左右或上下对称的椭圆。这些圆的最长透视直径称长径,为水平线或铅垂线。
d.垂直于画面的水平圆在主垂线左右时的透视形不是对称的椭圆,而有些歪斜,长径也不是水平状态;离主垂线意远愈歪斜。
e.垂直于画面的直立圆比视平线高或低于视平线时,透视形也不是上下对称的椭圆,而有些歪斜,长径也不是铅垂状态;离视平线愈远,即愈高或愈低时愈歪斜。
垂直于画面的水平圆和直立圆愈远,它的透视形愈接近为对称的椭圆,根据这一规律,由于我们平时作画相对来说一般距离较远,再加上要照顾一般人的视觉心理,因此在注意圆的透视规律的同时,不要不恰当的过分强调至斜现象,特别是水平圆。
(3)圆的透视宽窄变化
垂直于画面的水平圆位于视平线上下时,距视平线愈远愈宽,意接近视平线意窄,长径渐趋水平:与视平线等高时就成为一条横线。
(4)同心圆的透视特征
同一个圆心的大小不同的圆,叫做同心圆。同心圆大小两个圆周之间的距离宽窄的透视特征是:两端宽,远端窄,近端宽度居中。
(5)等分圆周的透视规律
等分后的圆周两端密,中间疏。由此等分的圆柱曲面中间宽、两边窄。
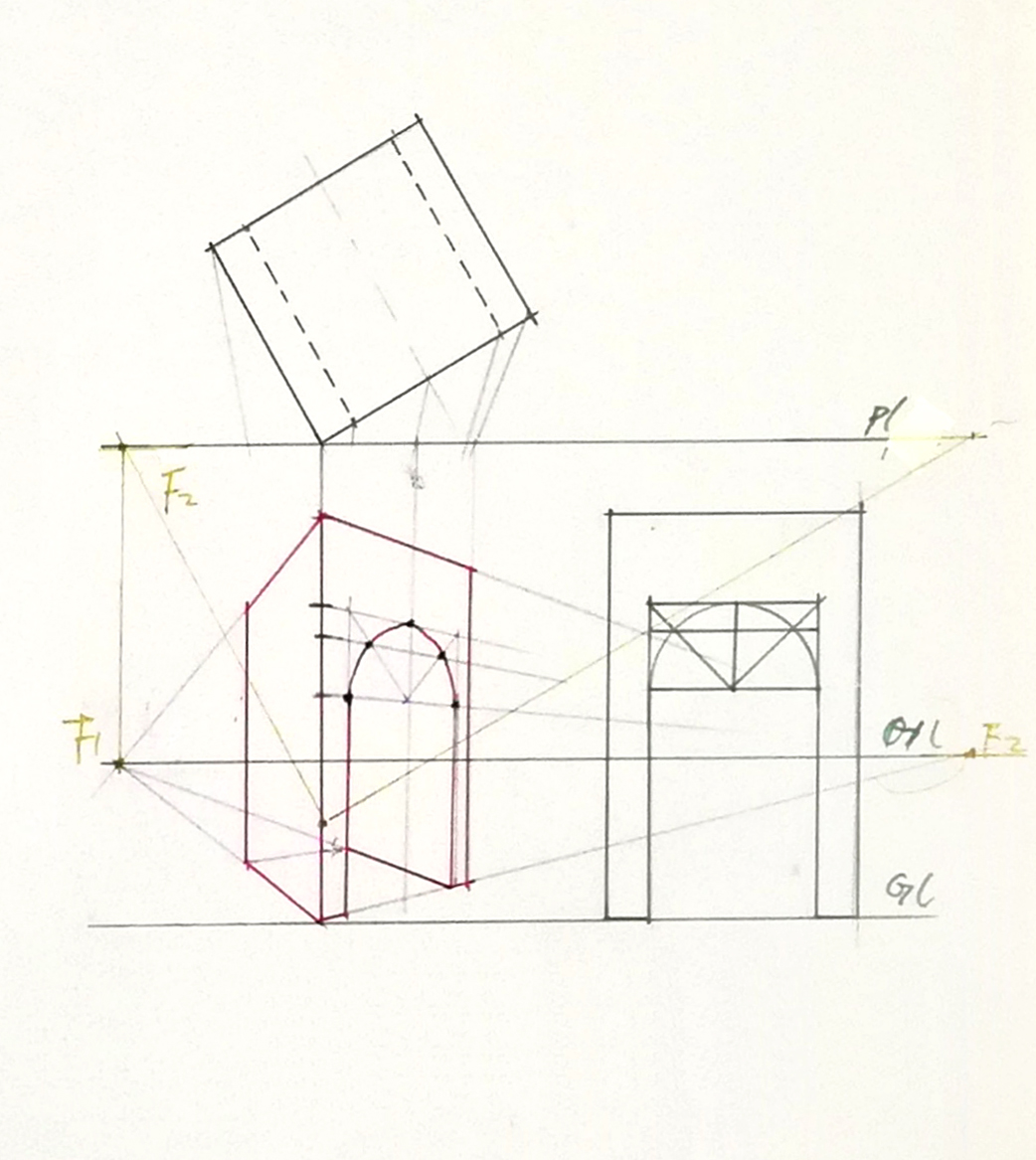
(6)半圆拱门的成角透视画法
首先根据门的宽度和高度(包括半圆拱)画出矩形的透视,然后在门的上部透视等分门的宽度画出两个正方形的透视,得到半圆拱的切点;再作出两正方形的对角线与半圆弧交点的透视1和2。把这五个点用曲线光滑地连接起来,即为半圆的透视。最后画出墙的厚度,用同样方法画出后面的半圆形。被墙遮去的部分也要用细线画出,这样前后半圆的相互关系才能画准确。

(7)不规则曲线透视
不规则曲线透视的基本特征
a、平面曲线的透视,仍然体现出近大远小的特征,其透视图形仍然是曲线,只有平面曲线所在的面与视轴和视平线(平视时为地平线)重叠时,则平面曲线为一条线。
b、平面曲线不平行于画面时,平面曲线发生近大远小的近疏远密的变化。
c.平面曲线平行于画面时,平面曲线不发生透视形状变化,保持原状。
不规则曲线透视的画法
在平面曲线的平面图上,用直线分割的方形网格将平面曲线分割,使平面曲线部分容纳在网格之中,网格的大小度量单位仍以人的高度作为基本度量单位。根据透视的基本规律,在平行透视、成角透视、倾斜透视等不同的透视画面中将网格建立,再把网格中的平面曲线按分割后的坐标位置近似画出,便得到平面曲线的透视。
曲面体透视的作图方法
(1)圆柱体透视的画法
a.平视时,采用平视透视画法先画出圆柱体的中心轴和圆面的直径,中心轴的长度为圆柱体的长度当中心轴为原线时,不发生透视变化,且保持原状:当中心轴为变线时,根据灭点定理确定消失点,用距点和测点确定中心轴长度。
b.随意选用画圆的几种方法中的种,建立圆柱体的可见截面和不可见截面。
c.在平视时圆柱的直径为原线时,其大小用等比方法确定。
d.圆柱体中心主向的轮廓线与中轴平行。中心轴为原线时,其对应的轮廓线与原线保持原状:中心轴为变线时,其对应的轮廓线消失到同消失点。
采用八点法、十二点法作圆柱的透视,等于把圆柱放在四棱体之内,是在四棱体基础上进行的。
(2)球体透视的画法
球体透视的特征
a.球的任何一个截面均为圆形,相当于直径不同的圆形在中轴上的组合、叠加和旋转。
b。近中心投影作图法对球(包括直径不同的圆)进行透视会发现只有视轴通过球心的圆球轮廓才是正圆,其余截面则为椭圆。但如果圆球的位置靠近心点,大约在60°的视角范围内眼力很难看出轮廓是椭圆,因此,在绘画作品中一般把圆球的透视画成正圆形。
画法
a.根据球的透视特点,只有视心轴线通过球心的圆才是正圆,当附着在球上的圆的直径平行于画面时,有几种情况,圆高于视平线或低于视平线,在视平线的左边或者右边。
b.通过球心的任何截面均为等大的标准圆,直径相等,面积相等。
c.当附着在球体上的圆的直径与画面不平行时,画法如下:
(1)根据灭点定理和假设直径与画面所成的角度,找出任何一个截面圆的直径。
(2)过直径作一垂直线,使其与视平线相交于一点,过直径两端引线向这一点消失。
(3)用任何一种求圆法画出截面圆。
2.8.2 圆的透视与建筑细部透视
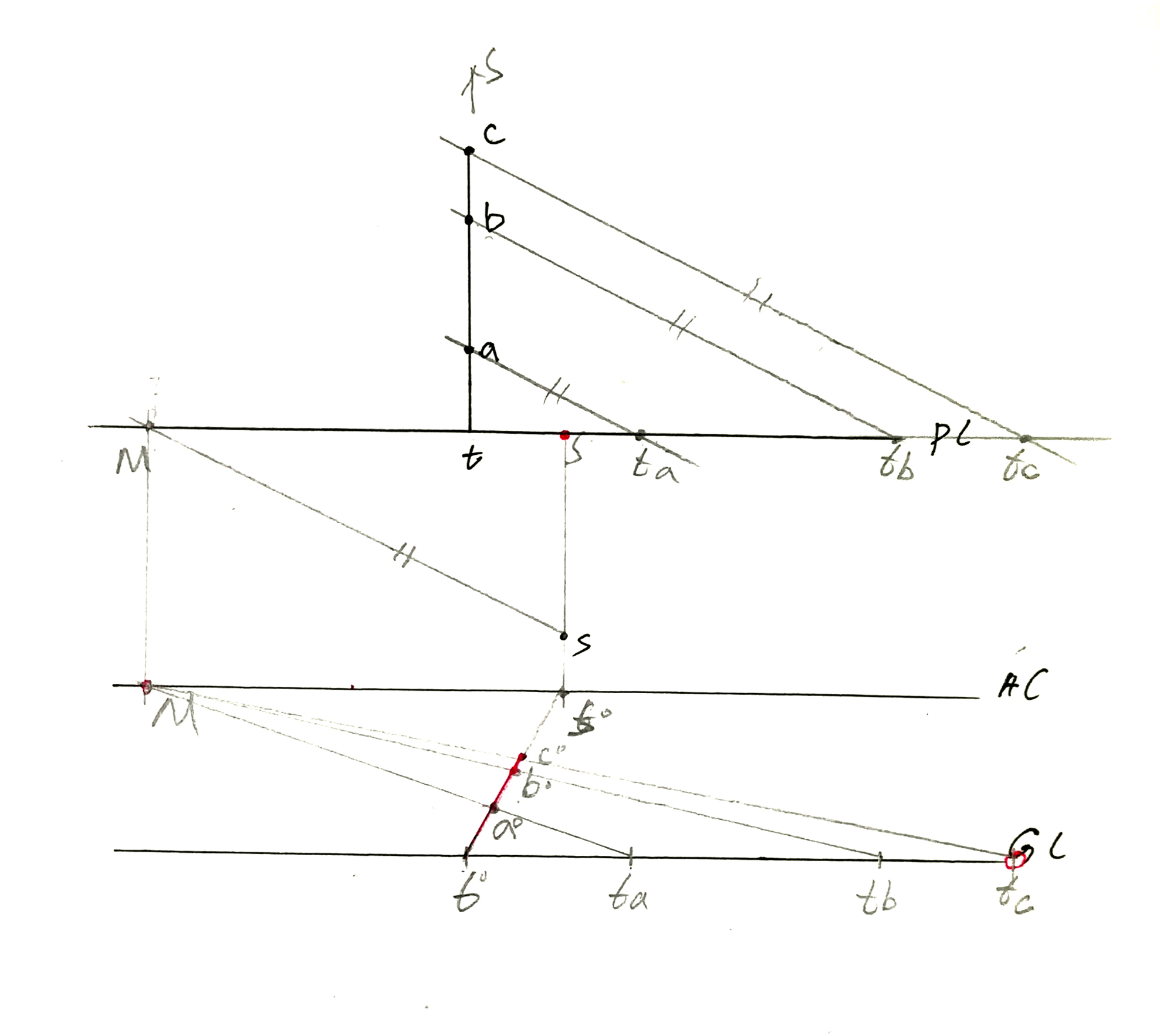

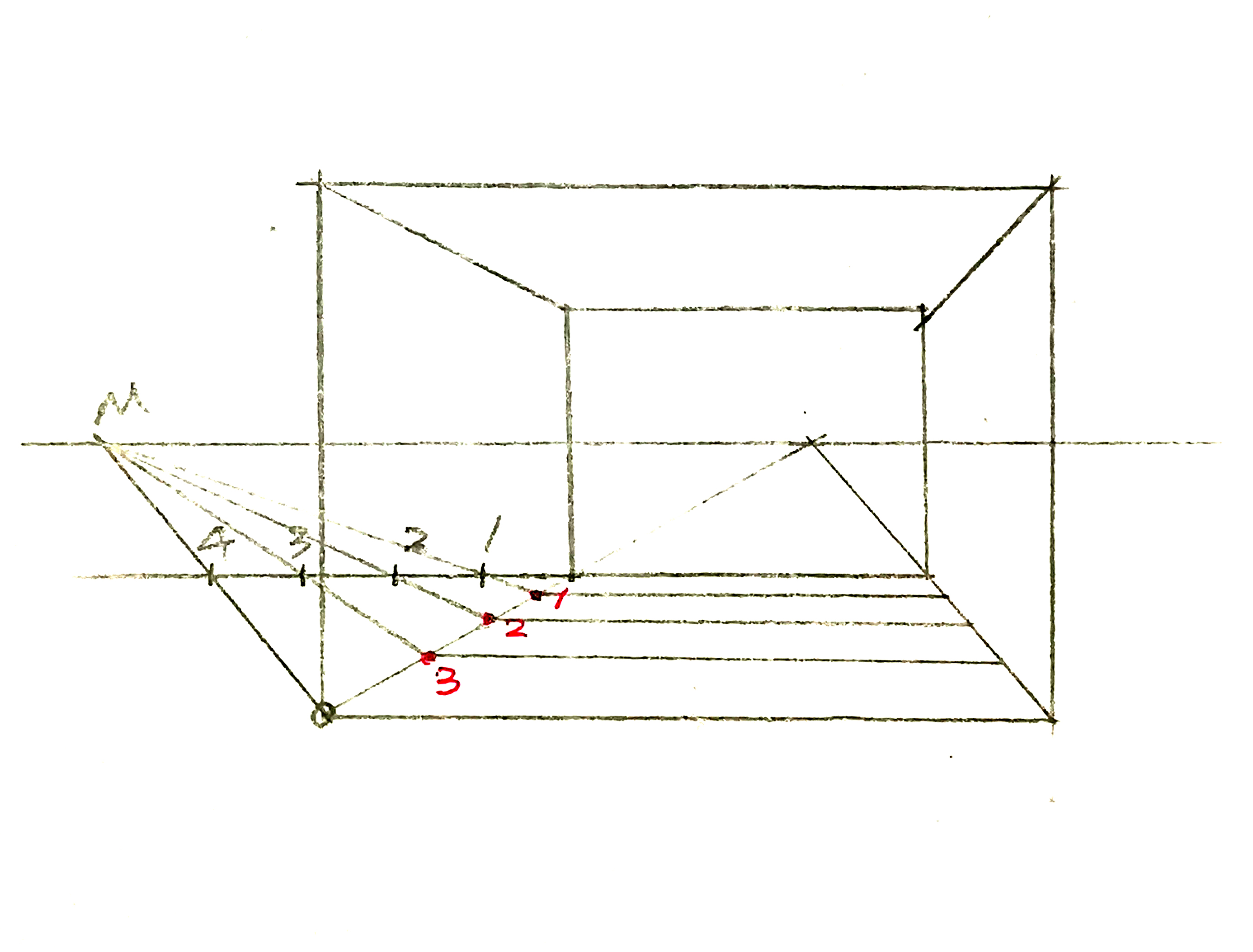



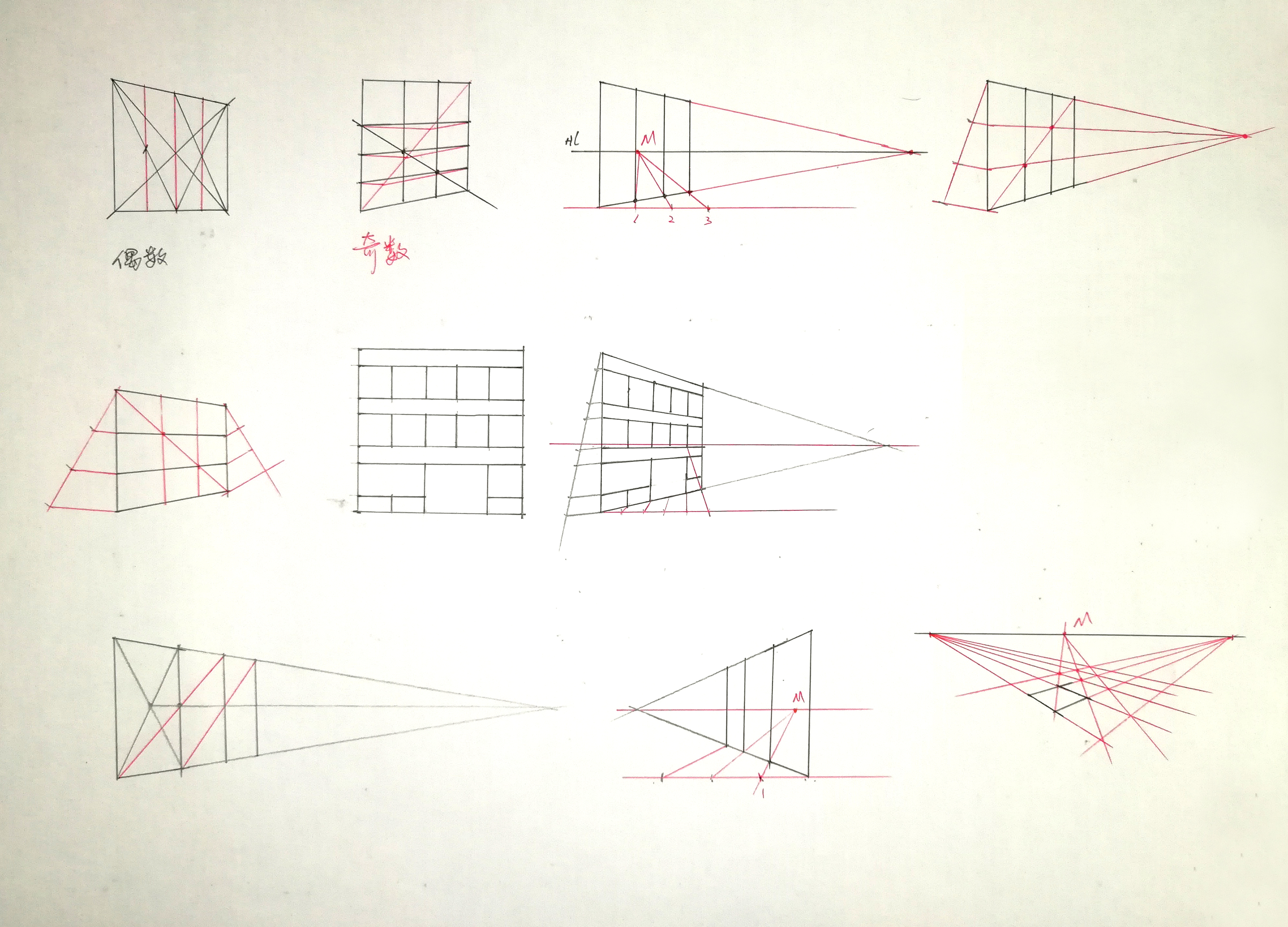
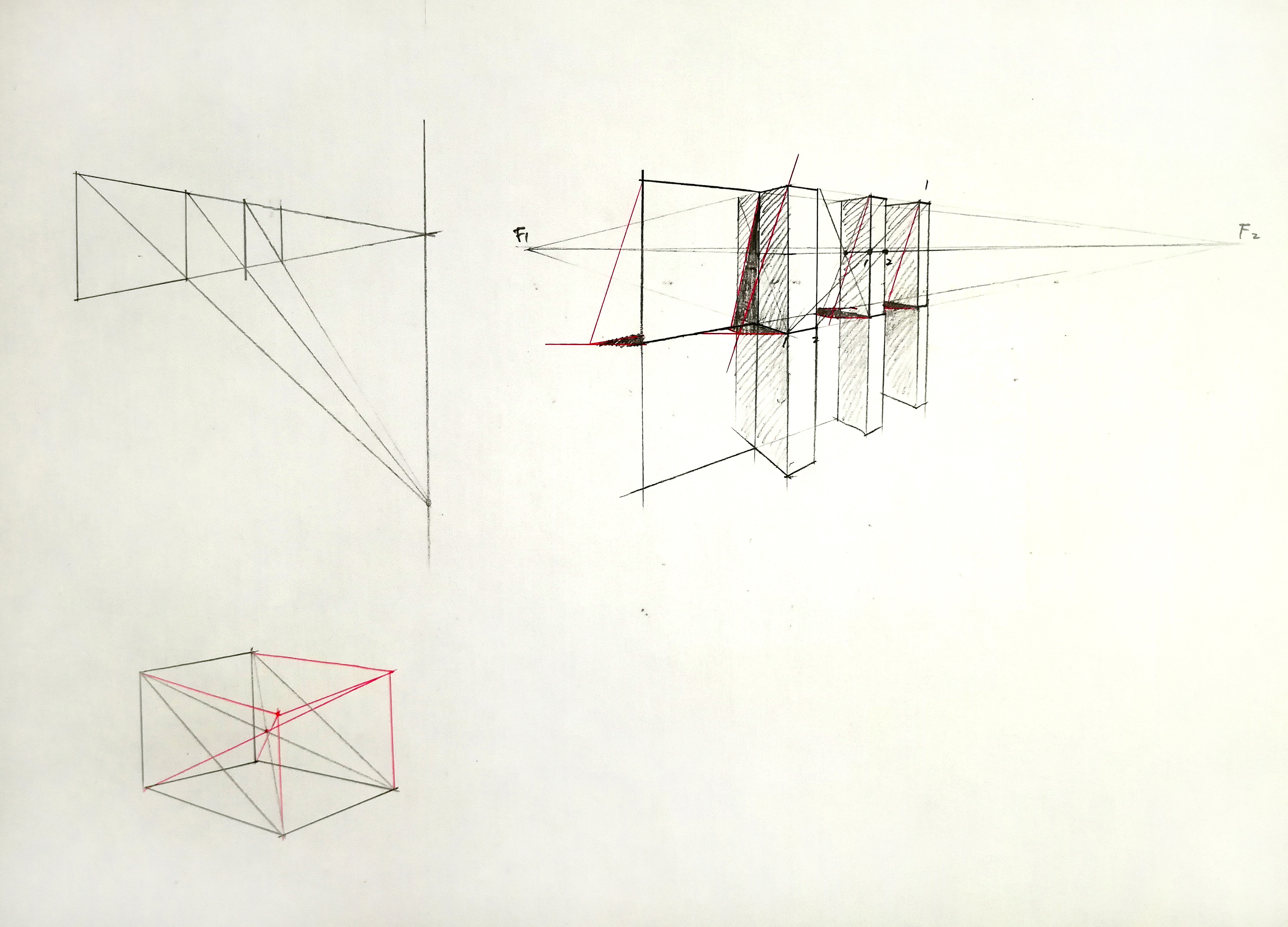
微角透视的作图方法与步骤

展示效果图铅笔稿(崔笑声)


