最大流问题
-
1 课件
-
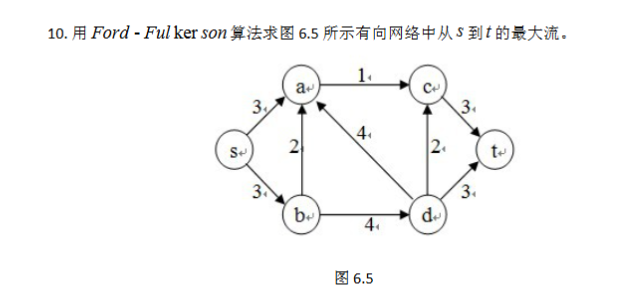
2 课后习题
上一节
下一节
最大流问题
网路流一般在有向图上讨论,弧的方向为流的方向;
定义网路上支路的容量为其最大通过能力,记为 rij ,支路上的实际流量记为 xij ,网络流为所有通过弧的流量的集合。
图中规定一个发点s,一个收点t;
节点没有容量限制,流在节点不会存储。
可 行 流
满足以下条件的流称为可行流:
1、每一个节点流量平衡(流进=流出)
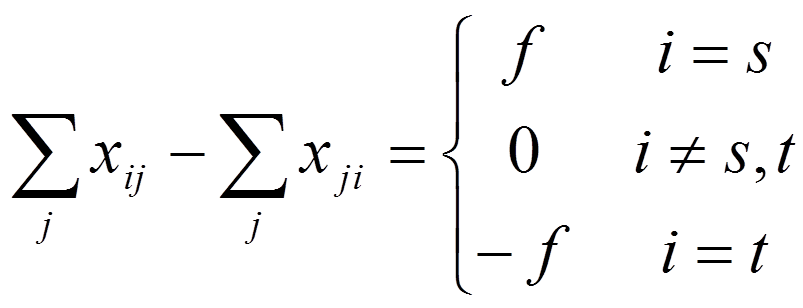
2、0≤xij ≤cij(容量限制)总流量最大的可行流为最大流。
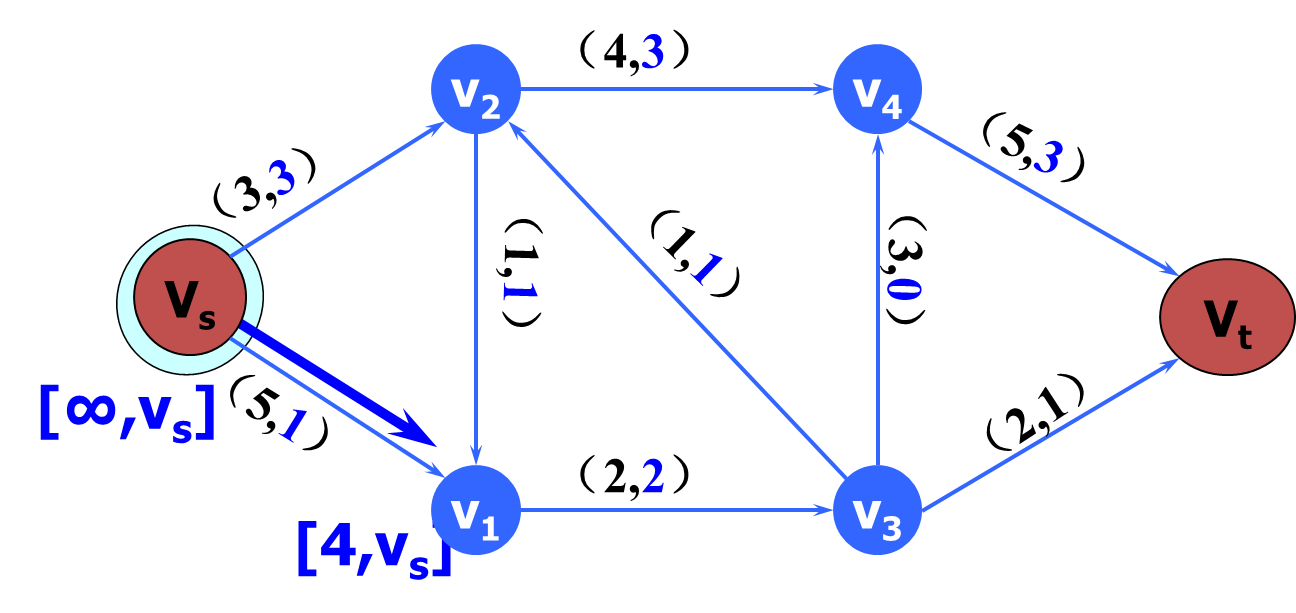
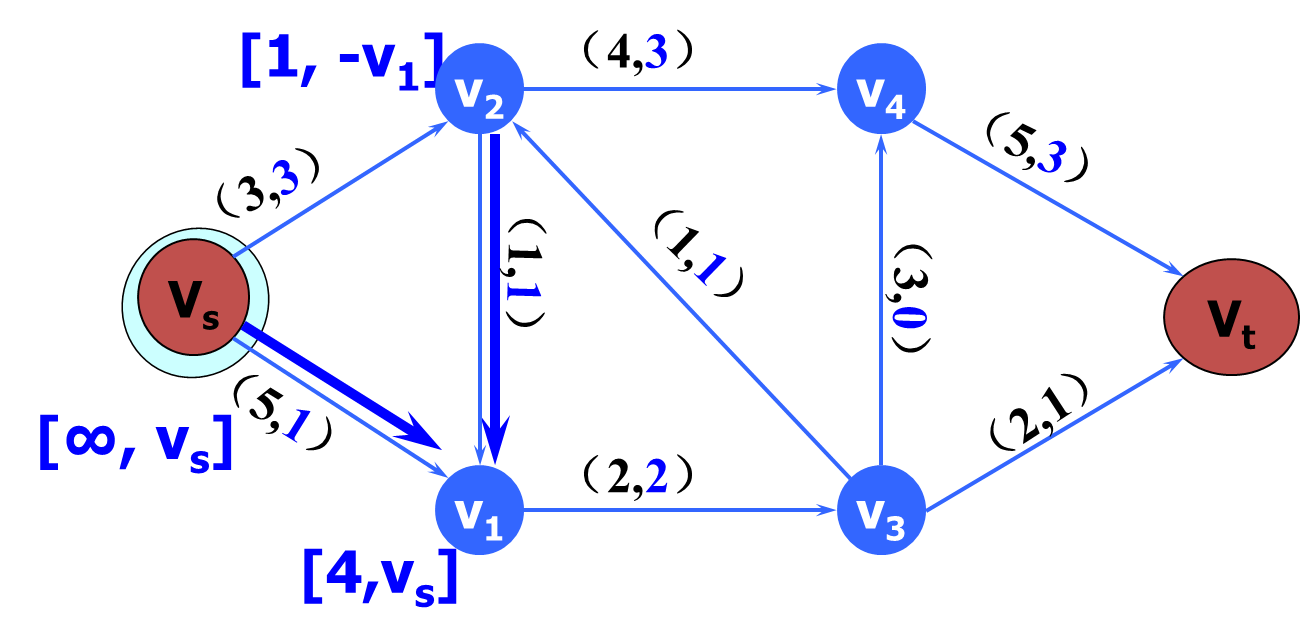
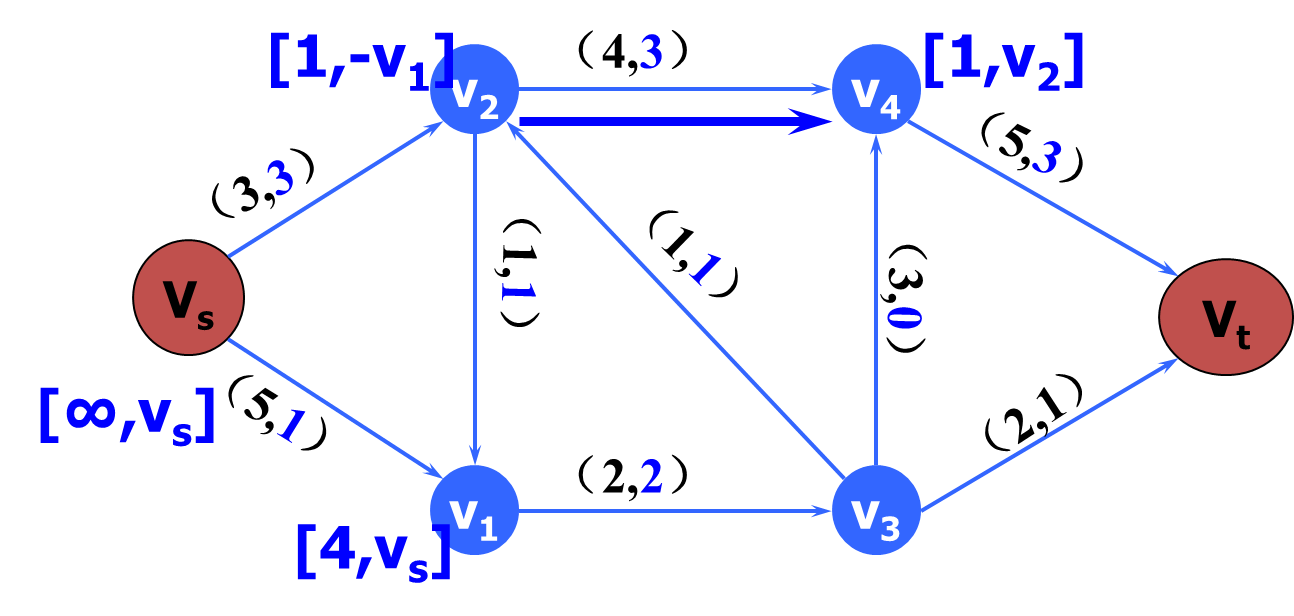
链的前向弧,后向弧
μ是网络D中一条从始点Vs到终点Vt的链,在链中与链的方向一致的弧称为链的前向弧,在链中与链的方向相反的弧称为链的后向弧。

饱和弧、不饱和弧


截集与截集容量
定义:把网络的点集分割为两个非空集合S和S,且S包含 Vs 点,另一个包含 Vt 点 ,则把始点在S中,终点在S中的弧的集合称为分离Vs和Vt的一个截集。
截量:是指截集中所有弧的容量之和;
福特-富克森定理:网路的最大流等于最小截集容量。
增广链(augmenting path)


基本定理:
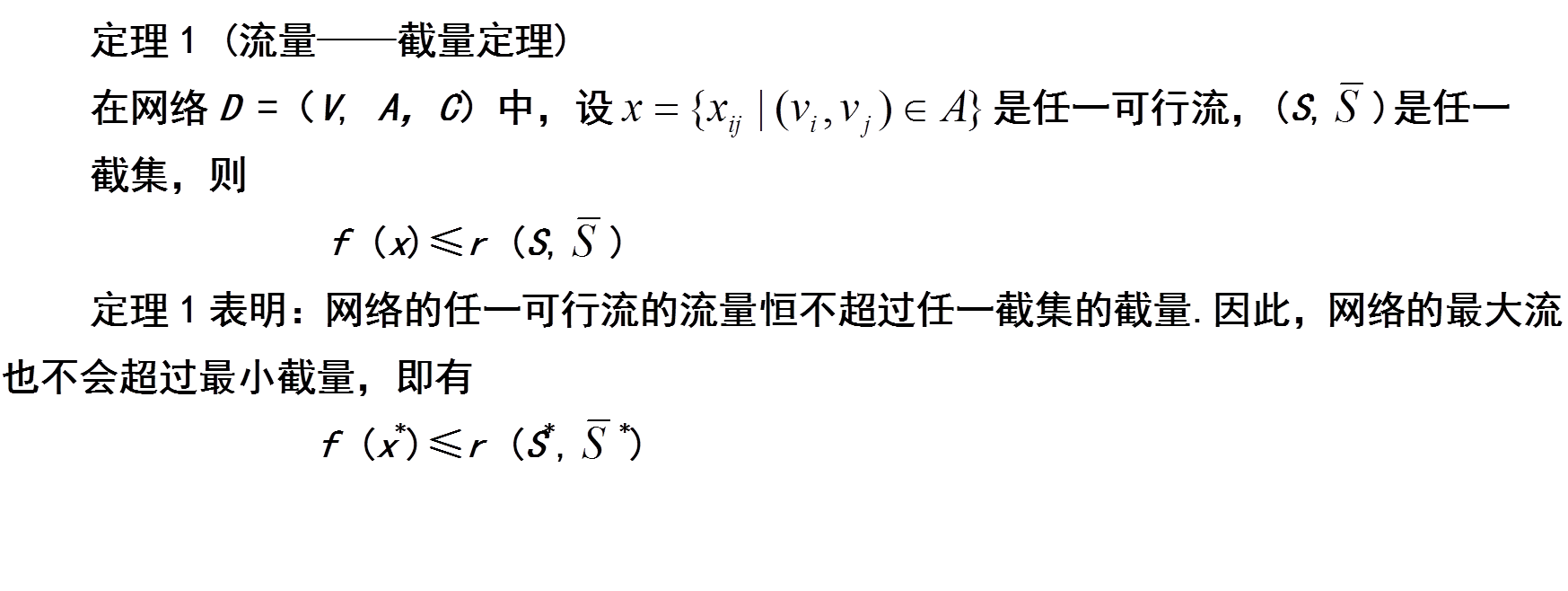
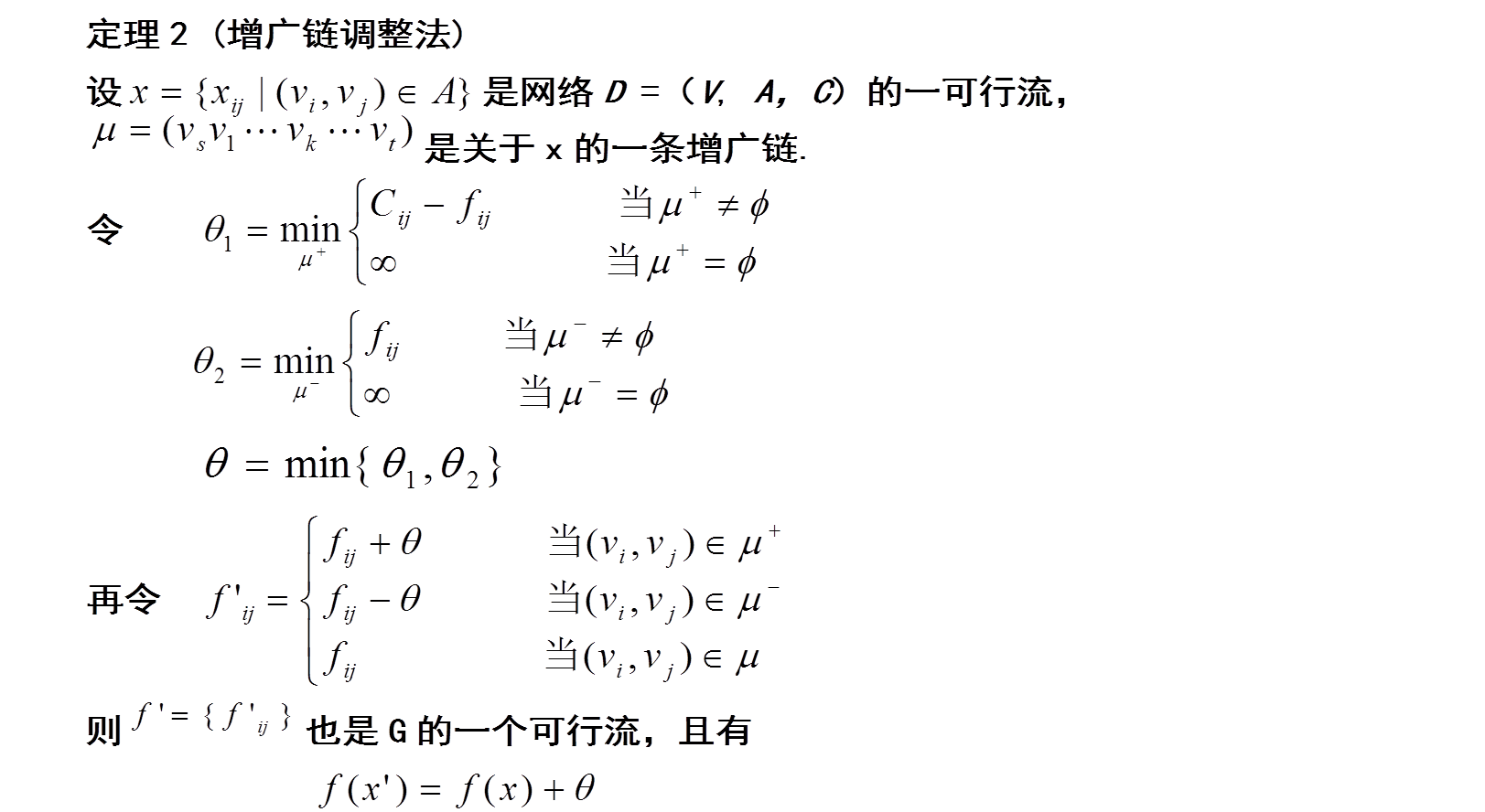
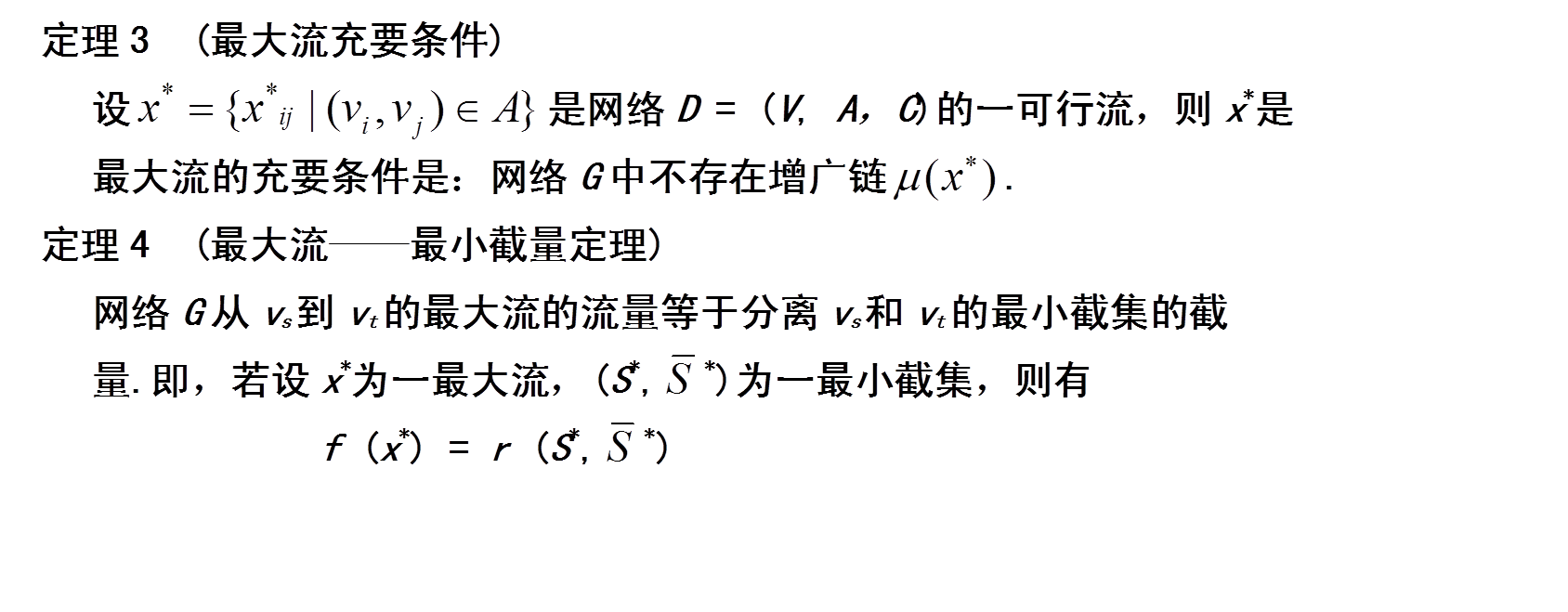
求最大流方法——标号法